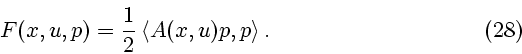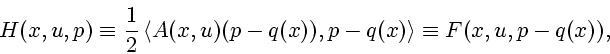С особой поверхностью можно соотнести следующие две
С особой поверхностью можно соотнести следующие две ![]() -мерные поверхности
в пространстве
-мерные поверхности
в пространстве ![]() векторов
векторов ![]() :
:
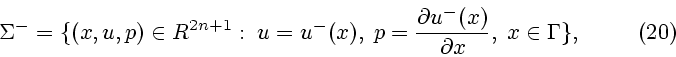
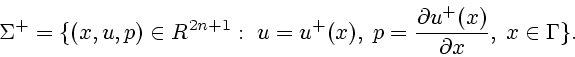
Предварительно преобразуем условия Вейерштрасса-Эрдмана, используя более
удобные обозначения. Условия (19) симметричны относительно обеих гладких
ветвей решения ![]() ,
, ![]() . Однако при построении решения (численном или
аналитическом) одна из ветвей может быть найдена до построения поверхности
. Однако при построении решения (численном или
аналитическом) одна из ветвей может быть найдена до построения поверхности
![]() , а для построения другой ветви требуется знание поверхности
, а для построения другой ветви требуется знание поверхности ![]() .
В обозначении ветви
.
В обозначении ветви ![]() опустим знак плюс, а ветвь
опустим знак плюс, а ветвь ![]() будем обозначать
через
будем обозначать
через ![]() , используя для градиентов обозначе-
, используя для градиентов обозначе-
ния ![]() .
.
Для определенности будем полагать известной ветвь ![]() ,
, ![]() , точнее,
некоторое ее гладкое расширение на область
, точнее,
некоторое ее гладкое расширение на область ![]() . Подставив значения
. Подставив значения ![]() в левую часть равенств (19), будем рассматривать эти части как функции
величин
в левую часть равенств (19), будем рассматривать эти части как функции
величин ![]() , обозначаемые соответственно через
, обозначаемые соответственно через ![]() ,
, ![]() .
Искомым объектом будем считать поверхность
.
Искомым объектом будем считать поверхность ![]() в (20). На ней оказываются
выполненными следующие три необходимых условия оптимальности:
в (20). На ней оказываются
выполненными следующие три необходимых условия оптимальности:
Другое наблюдение состоит в том,
что второе условие Вейерштрас-
са-Эрдмана выражается через первое условие
в терминах скобок Якоби следующим образом:
Соотношение (22) предлагает инвариантную интерпретацию условий Вейерштрасса-Эрдмана.
Таким образом, условия (21) определяют в ![]() следующее многообразие
следующее многообразие
![]() , вообще говоря, коразмерности
, вообще говоря, коразмерности ![]() :
:
Некоторые задачи в теории нелинейных уравнений в частных производных первого
или второго порядка на геометрическом языке сводятся к отысканию интегральных
поверхностей ![]()
![]() -формы
-формы
![]() или их проекций
или их проекций ![]() на подпространство
на подпространство ![]() . При этом общая размерность
. При этом общая размерность ![]() и
и ![]() может быть равна
может быть равна ![]() . Поверхности (20), в частности, имеют размерность
. Поверхности (20), в частности, имеют размерность
![]() . Задача Коши для уравнения первого порядка формулируется в терминах
. Задача Коши для уравнения первого порядка формулируется в терминах
![]() -мерной поверхности
-мерной поверхности ![]() , причем начальные условия определяют
, причем начальные условия определяют
![]() -мерную поверхность
-мерную поверхность
![]() (начальную полоску).
Известно, что построение
(начальную полоску).
Известно, что построение ![]() , а вместе с ней и гладкого решения
уравнения
, а вместе с ней и гладкого решения
уравнения ![]() , сводится к интегрированию системы регулярных
(классических) характеристик
, сводится к интегрированию системы регулярных
(классических) характеристик
Метод сингулярных характеристик состоит в том, что система (24) обобщается для
построения поверхностей ![]() меньшей размерности. Приведем описание метода
для случая коразмерности
меньшей размерности. Приведем описание метода
для случая коразмерности ![]() . В этом случае искомая
. В этом случае искомая ![]() -мерная поверхность
-мерная поверхность
![]() и начальная
и начальная ![]() -мерная поверхность
-мерная поверхность ![]() должны принадлежать
подмногообразию
должны принадлежать
подмногообразию
![]() коразмерности
коразмерности ![]() :
:
Полную формулировку теоремы, гарантирующей единственность (в малом) искомой
поверхности ![]() , можно найти в [10, 11]. Основное
требование к функциям
, можно найти в [10, 11]. Основное
требование к функциям ![]() сводится к тому, чтобы вектор
сводится к тому, чтобы вектор
![]() был трансверсален (не касался) проекции
был трансверсален (не касался) проекции ![]() начальной
поверхности
начальной
поверхности ![]() . Из этого, в частности, следует, что все коэффициенты
линейной комбинации (26) (скобки Якоби) не могут одновременно обратиться в
ноль.
. Из этого, в частности, следует, что все коэффициенты
линейной комбинации (26) (скобки Якоби) не могут одновременно обратиться в
ноль.
Используя в (25), (26) функции (23), приняв
![]() и записав
систему (24) в терминах полученного
и записав
систему (24) в терминах полученного ![]() , придем к следующей системе
сингулярных характеристик:
, придем к следующей системе
сингулярных характеристик:
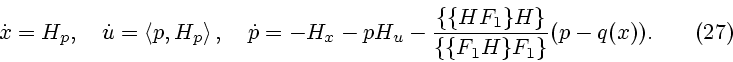
Система (27) описывает один из типов сингулярных характеристик нелинейного
уравнения в частных производных первого порядка
![]() . Роль системы
(27) для уравнения второго порядка (3) заключается в том, что она описывает
распространение возмущений (негладкости) решения; с ее помощью, в частности,
можно находить область границы
. Роль системы
(27) для уравнения второго порядка (3) заключается в том, что она описывает
распространение возмущений (негладкости) решения; с ее помощью, в частности,
можно находить область границы ![]() , которая влияет на значение решения
в данной точке облас-
, которая влияет на значение решения
в данной точке облас-
ти ![]() .
.
В теории дифференциальных игр система (27) является сингулярной характеристикой уравнения Беллмана-Айзекса и описывает так называемые особые экивокальные траектории.
В некоторых задачах математической физики лагранжиан является квадратичной
функцией вектора ![]() :
: