

Next: 3 Построение особой поверхности,
Up: MELIK
Previous: 1 Введение
Рассмотрим следующую вариационную задачу в области относительно неизвестной
(искомой) скалярной функции 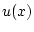 ,
,
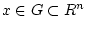 :
:
Конкретный вид граничных условий ![$B[u(x)] = 0$](img8.gif) , который зависит от типа задачи
и включает задание на различных частях границы значений самой функции или
её частных производных, для дальнейших рассмотрений не существенен.
Функционал (1) рассматривается на множестве
, который зависит от типа задачи
и включает задание на различных частях границы значений самой функции или
её частных производных, для дальнейших рассмотрений не существенен.
Функционал (1) рассматривается на множестве
элементами которого являются пары 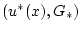 , состоящие из непрерывной
функции
, состоящие из непрерывной
функции 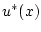 , определенной и дважды кусочно-непрерывно дифференцируемой
в области
, определенной и дважды кусочно-непрерывно дифференцируемой
в области 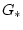 . Для краткости это будем обозначать как
. Для краткости это будем обозначать как
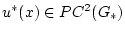 .
Область
.
Область 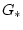 , вообще говоря, своя для каждой функции. Таким образом,
рассматривается задача с нефиксированной (варьируемой) границей.
Лагранжиан
, вообще говоря, своя для каждой функции. Таким образом,
рассматривается задача с нефиксированной (варьируемой) границей.
Лагранжиан 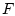 предполагается непрерывно дифференцируемым достаточное число
раз.
предполагается непрерывно дифференцируемым достаточное число
раз.
Известно, что дважды дифференцируемое решение задачи (1) удовлетворяет
уравнению Эйлера-Лагранжа - квазилинейному дифференциальному уравнению в
частных производных второго порядка
Решением вариационной задачи (1), вообще говоря, может быть негладкая
функция класса (2). Такие функции удовлетворяют уравнению Эйлера только
в точках дифференцируемости. Без дополнительных требований на поверхностях
потери гладкости решение, вообще говоря, может быть неединственным.
Для того чтобы рассматривать решения уравнения (3) в классе кусочно гладких
функций (2), определим решение как функцию класса 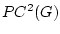 , удовлетворяющую
равенству
, удовлетворяющую
равенству
для всех допустимых вариаций 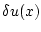 функции
функции 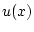 . Здесь
. Здесь 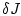 -
первая вариация функционала (1), соответствующая вариации функции
-
первая вариация функционала (1), соответствующая вариации функции
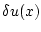 . Класс допустимых вариаций
. Класс допустимых вариаций 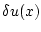 будет уточнен ниже.
Таким образом, обобщенное решение в точках гладкости удовлетворяет уравнению
(3), а в точках потери гладкости - некоторым другим следствиям из
соотно-
будет уточнен ниже.
Таким образом, обобщенное решение в точках гладкости удовлетворяет уравнению
(3), а в точках потери гладкости - некоторым другим следствиям из
соотно-
шения (4).
Отметим, что для уравнений в частных производных второго порядка вида (3),
т.е. являющихся уравнением Эйлера-Лагранжа, можно определить обобщенное
решение на основе вариационного принципа. Для уравнений другого вида
обобщенное решение определяется с привлечением других свойств математического
или физического характера.
Область определения функционала (1), множество 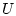 в (2), не является линейным
пространством, поскольку область
в (2), не является линейным
пространством, поскольку область 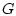 подвижна. Поэтому первая вариация
определяется не как производная по направлению, а с помощью дифференцирования
вдоль кривой на многообразии
подвижна. Поэтому первая вариация
определяется не как производная по направлению, а с помощью дифференцирования
вдоль кривой на многообразии 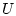 , которая представляет собой однопараметрическое
семейство допустимых функций вида:
, которая представляет собой однопараметрическое
семейство допустимых функций вида:
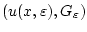 ,
,
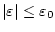 .
Рассмотрим семейство обратимых преобразований друг в друга
.
Рассмотрим семейство обратимых преобразований друг в друга 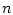 -мерных
пространств
-мерных
пространств 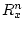 ,
, 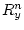 (однопараметрическую группу)
(однопараметрическую группу)
где
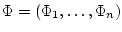 ,
,
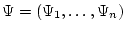 - гладкие
вектор-функции.
- гладкие
вектор-функции.
Определим также вектор-функцию
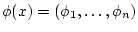 и область
и область
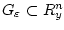
Зафиксируем два элемента множества 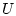 :
: 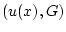 ,
, 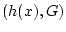 , где
, где
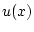 ,
, 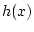 - гладкие функции, причем
- гладкие функции, причем 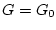 . Определим однопараметрическое
семейство допустимых функций соотношением
. Определим однопараметрическое
семейство допустимых функций соотношением
где
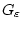 задано в (6). При
задано в (6). При
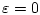 получаем
получаем
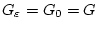 и
и
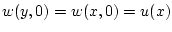 , поскольку
, поскольку 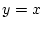 . Для функции
. Для функции 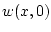 будем использовать
также обозначение
будем использовать
также обозначение 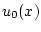 , с тем чтобы рассматриваемая точка многообразия
, с тем чтобы рассматриваемая точка многообразия 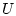 имела вид
имела вид 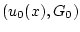 . Таким образом, семейство (7) представляет собой
некоторую кривую на многообразии
. Таким образом, семейство (7) представляет собой
некоторую кривую на многообразии 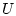 , проходящую через точку
, проходящую через точку 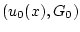 .
.
Первая вариация функционала (1), соответствующая допустимой функции
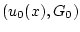 и вариации
и вариации 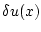 (уточняемой ниже) этой функции,
определяется равенством
(уточняемой ниже) этой функции,
определяется равенством
Для вычисления производной по 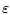 удобно привести кратный интеграл по
переменной
удобно привести кратный интеграл по
переменной 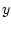 в области
в области
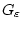 путем замены переменных к интегралу по
переменной
путем замены переменных к интегралу по
переменной 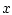 в стандартной области
в стандартной области 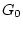 , не зависящей от
, не зависящей от 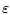 ,
,
где
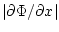 - якобиан преобразования (5). Дифференцирование по
- якобиан преобразования (5). Дифференцирование по
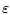 в (8) сводится к дифференцированию подынтегрального выражения в (9):
в (8) сводится к дифференцированию подынтегрального выражения в (9):
Преобразуя это выражение, используя свойства группы (5), можно получить
следующую формулу для первой вариации:
Производная
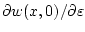 выражается через функции
выражается через функции 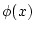 ,
, 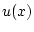 и
и 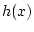 следующим образом:
следующим образом:
Функция 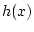 , вообще говоря, не исчезает на границе
, вообще говоря, не исчезает на границе 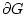 и должна быть
согласована с граничными условиями в (1). Таким образом, первая вариация
(11) представляет собой линейный функционал от двух функций: скалярной функции
и должна быть
согласована с граничными условиями в (1). Таким образом, первая вариация
(11) представляет собой линейный функционал от двух функций: скалярной функции
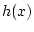 и векторной функции
и векторной функции 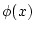 , которые, по определению, в совокупности
составляют вариацию номинальной функции
, которые, по определению, в совокупности
составляют вариацию номинальной функции
Используя формулу Остроградского-Гаусса и соотношение (12), можно привести
формулу (11) для первой вариции к виду
где 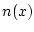 - внешняя нормаль к границе области
- внешняя нормаль к границе области 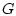 в точке
в точке
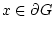 ,
,
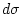 - элемент площади поверхности. Здесь предполагается, что функция
- элемент площади поверхности. Здесь предполагается, что функция
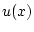 дважды гладкая, а поверхность
дважды гладкая, а поверхность 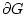 - кусочно-гладкая.
Из формулы (14) видно, что для первой вариации функционала существенны значения
функции
- кусочно-гладкая.
Из формулы (14) видно, что для первой вариации функционала существенны значения
функции 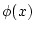 лишь в граничных точках области
лишь в граничных точках области 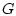 .
.
Для вариаций (13) с фиксированной границей и граничными значениями, т.е. когда
функция 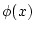 исчезает во всей области, а функция
исчезает во всей области, а функция 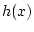 - лишь на границе
- лишь на границе
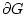 , равенство нулю первой вариации (14) влечет за собой уравнение Эйлера
(3) (основная лемма вариационного исчисления).
, равенство нулю первой вариации (14) влечет за собой уравнение Эйлера
(3) (основная лемма вариационного исчисления).
Пусть пара 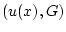 является решением задачи (1) и существует гладкая
поверхность
является решением задачи (1) и существует гладкая
поверхность
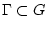 , разделяющая область
, разделяющая область 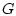 на две открытые
подобласти
на две открытые
подобласти 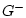 ,
, 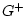 :
:
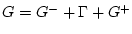 . Предположим, что функция
. Предположим, что функция 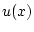 является непрерывной в области
является непрерывной в области 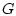 и дважды гладкой в каждой из областей
и дважды гладкой в каждой из областей
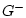 ,
, 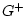 , а ее градиент терпит разрыв на
, а ее градиент терпит разрыв на 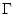 . Через
. Через
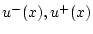 будем обозначать ограничение функции
будем обозначать ограничение функции 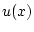 на области
на области 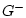 ,
, 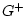 ,
а для их градиентов введем обозначение
,
а для их градиентов введем обозначение
Итак,
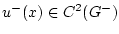 ,
,
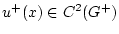 , причем векторы
, причем векторы
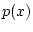 ,
, 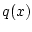 , по предположению, имеют непрерывное продолжение из области
, по предположению, имеют непрерывное продолжение из области
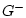 ,
, 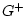
вплоть до поверхности 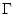 .
.
Для вывода необходимых условий оптимальности представим функционал 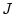 как
сумму двух функционалов
как
сумму двух функционалов 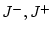 , определенных в областях
, определенных в областях 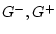 соответственно. Таким образом,
соответственно. Таким образом,
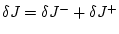 , причем
вариации
, причем
вариации 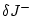 ,
, 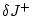 соответствуют вариациям
соответствуют вариациям
Последние два равенства здесь следуют из непрерывности решения 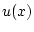 в области
в области
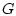 . Предположим, что граница
. Предположим, что граница 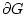 исходной области фиксирована, функции
исходной области фиксирована, функции
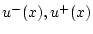 удовлетворяют уравнению Эйлера в областях
удовлетворяют уравнению Эйлера в областях 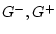 , их
значения на
, их
значения на 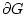 фиксированы, а варьируются только общая часть
фиксированы, а варьируются только общая часть 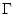 границ областей
границ областей 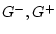 и общее значение этих функций на
и общее значение этих функций на 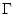 .
Первая вариация функционала, которая должна обращаться в нуль на всех допустимых
вариациях (16), принимает вид
.
Первая вариация функционала, которая должна обращаться в нуль на всех допустимых
вариациях (16), принимает вид
По основной лемме вариационного исчисления из условия 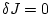 следует,
что скалярный множитель при
следует,
что скалярный множитель при 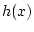 и векторный множитель при
и векторный множитель при 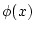 исчезают на
исчезают на 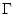 :
:
Заметим, что вследствие непрерывности функции 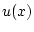 вектор
вектор 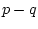 ортогонален
поверхности
ортогонален
поверхности 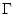 , т.е. коллинеарен вектору
, т.е. коллинеарен вектору 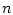 . Поэтому для некоторой
ненулевой скалярной величины
. Поэтому для некоторой
ненулевой скалярной величины 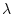 имеет место равенство
имеет место равенство
которое, в частности, приводит к соотношению
Данное равенство вместе с первым равенством (18) позволяет привести второе
равенство (18) к виду
означающему, что левая часть второго равенства (18) также коллинеарна вектору
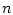 . Поскольку
. Поскольку  - ненулевой (единичный) вектор, то должен обратиться в ноль
скалярный множитель при нем. Таким образом, скалярное и векторное равенства
(18) эквивалентны двум следующим скалярным равенствам, выполненным на
поверхности
- ненулевой (единичный) вектор, то должен обратиться в ноль
скалярный множитель при нем. Таким образом, скалярное и векторное равенства
(18) эквивалентны двум следующим скалярным равенствам, выполненным на
поверхности  :
:
Равенства (19) представляют собой обобщение условий Вейерштрасса-Эрдмана
для угловой точки решения вариационной задачи с одной независимой переменной.


Next: 3 Построение особой поверхности,
Up: MELIK
Previous: 1 Введение
2003-05-08
![]() ,
,
![]() :
:
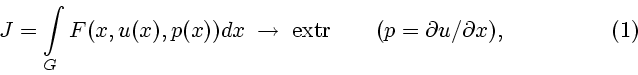
![\begin{displaymath}
B[u(x)]\Big\vert _{x\in \partial G} = 0.
\end{displaymath}](img7.gif)
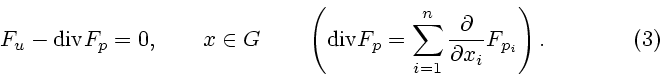
![]() в (2), не является линейным
пространством, поскольку область
в (2), не является линейным
пространством, поскольку область ![]() подвижна. Поэтому первая вариация
определяется не как производная по направлению, а с помощью дифференцирования
вдоль кривой на многообразии
подвижна. Поэтому первая вариация
определяется не как производная по направлению, а с помощью дифференцирования
вдоль кривой на многообразии ![]() , которая представляет собой однопараметрическое
семейство допустимых функций вида:
, которая представляет собой однопараметрическое
семейство допустимых функций вида:
![]() ,
,
![]() .
Рассмотрим семейство обратимых преобразований друг в друга
.
Рассмотрим семейство обратимых преобразований друг в друга ![]() -мерных
пространств
-мерных
пространств ![]() ,
, ![]() (однопараметрическую группу)
(однопараметрическую группу)
![]() и область
и область
![]()
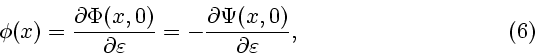
![]() :
: ![]() ,
, ![]() , где
, где
![]() ,
, ![]() - гладкие функции, причем
- гладкие функции, причем ![]() . Определим однопараметрическое
семейство допустимых функций соотношением
. Определим однопараметрическое
семейство допустимых функций соотношением
![]() и вариации
и вариации ![]() (уточняемой ниже) этой функции,
определяется равенством
(уточняемой ниже) этой функции,
определяется равенством
![\begin{displaymath}
\delta J[u(x);\delta u(x)]=\left. {dJ( \varepsilon )\over d \varepsilon }\right\vert _{ \varepsilon =0},
\eqno (8)
\end{displaymath}](img49.gif)
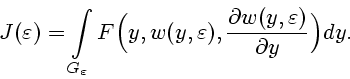
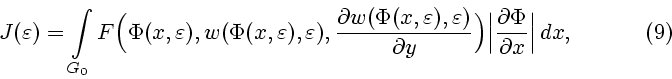
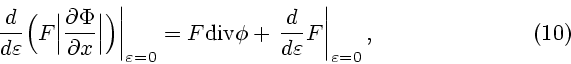
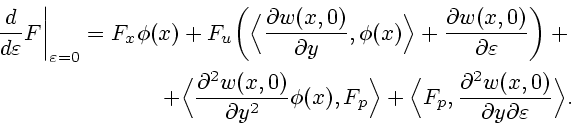
![\begin{displaymath}
\delta J = \int\limits_{G_0}\bigg[(F_u- \mathrm{div} F_p){ \...
...er \partial \varepsilon }F_p+F\phi(x)\Big)\bigg]dx. \eqno (11)
\end{displaymath}](img59.gif)
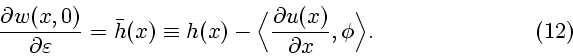
![\begin{displaymath}
\delta J = \int\limits_G[(F_u- \mathrm{div} F_p)\bar h(x)+
\mathrm{div} (\bar h(x)F_p+F\phi(x))]dx
\eqno (14)
\end{displaymath}](img65.gif)
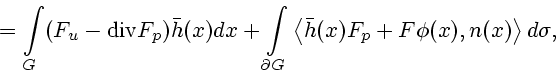
![]() исчезает во всей области, а функция
исчезает во всей области, а функция ![]() - лишь на границе
- лишь на границе
![]() , равенство нулю первой вариации (14) влечет за собой уравнение Эйлера
(3) (основная лемма вариационного исчисления).
, равенство нулю первой вариации (14) влечет за собой уравнение Эйлера
(3) (основная лемма вариационного исчисления).
![]() является решением задачи (1) и существует гладкая
поверхность
является решением задачи (1) и существует гладкая
поверхность
![]() , разделяющая область
, разделяющая область ![]() на две открытые
подобласти
на две открытые
подобласти ![]() ,
, ![]() :
:
![]() . Предположим, что функция
. Предположим, что функция ![]() является непрерывной в области
является непрерывной в области ![]() и дважды гладкой в каждой из областей
и дважды гладкой в каждой из областей
![]() ,
, ![]() , а ее градиент терпит разрыв на
, а ее градиент терпит разрыв на ![]() . Через
. Через
![]() будем обозначать ограничение функции
будем обозначать ограничение функции ![]() на области
на области ![]() ,
, ![]() ,
а для их градиентов введем обозначение
,
а для их градиентов введем обозначение
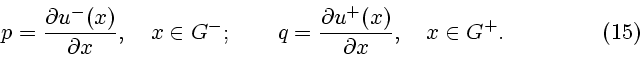
![]() как
сумму двух функционалов
как
сумму двух функционалов ![]() , определенных в областях
, определенных в областях ![]() соответственно. Таким образом,
соответственно. Таким образом,
![]() , причем
вариации
, причем
вариации ![]() ,
, ![]() соответствуют вариациям
соответствуют вариациям
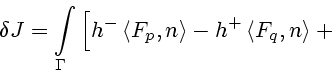
![]() следует,
что скалярный множитель при
следует,
что скалярный множитель при ![]() и векторный множитель при
и векторный множитель при ![]() исчезают на
исчезают на ![]() :
:
![]() вектор
вектор ![]() ортогонален
поверхности
ортогонален
поверхности ![]() , т.е. коллинеарен вектору
, т.е. коллинеарен вектору ![]() . Поэтому для некоторой
ненулевой скалярной величины
. Поэтому для некоторой
ненулевой скалярной величины ![]() имеет место равенство
имеет место равенство