3. Основные идеи построения информационных множеств

3.1 Введение дискретной схемы

При численном нахождении информационных множеств мы вынуждены использовать некоторую дискретизацию построений. Опишем основные элементы дискретизации.

Для нахождения множества ${\bf I}(t^*)$ сначала получим множество прогноза ${\bf G}(t^*)$. Чтобы построить ${\bf G}(t^*)$, разбиваем промежуток времени $[t_*, t^*]$ с постоянным шагом $\Delta$. Управления $u(\cdot)$ и $w(\cdot)$ считаем кусочно-постоянными на данном разбиении. При этом на каждом интервале $[t_i, t_{i+1})$ разбиения управляющие воздействия $u$, $w$ принимают лишь нулевые и крайние значения: $u \in \{ -1, 0, 1 \}$, $w \in \{ \mu_1, 0, \mu_2 \}$. Выбор таких значений определяется тем, что при построении оптимальных движений, формирующих границу множества достижимости (множества прогноза), в соответствии с принципом максимума Л. С. Понтрягина, используются крайние управляющие воздействия: $u=-1,1$; $w = \mu_1, \mu_2$. Значение $u=0$ реализуется на вырожденном оптимальном движении. Значение $w =0$ включено ради технического удобства.

Примем $t_1 = t_*$ и ${\bf G}(t_1) = {\bf I}(t_*)$. Множество прогноза ${\bf G}(t_{i+1})$ строим, опираясь на множество ${\bf G}(t_{i})$. Интегрируя систему (1.1), используем метод Эйлера с шагом $\Delta$.

Нахождение множеств ${\bf G}^\diamondsuit (t)$ и ${\bf G}_{\bar\psi, \bar V}(t)$ в схеме построения ИМ, изложенной в предыдущем разделе, упрощается следующим образом.

Формула для проекции на плоскость $\psi , V$ множества прогноза при фиксированных управляющих воздействиях $u, w$ (аналог (2.6)) запишется на момент $t_{i+1}$ в виде

$${\bf G}^\diamondsuit (t_{i+1}, u, w) = \{ (\psi + {\Delta k... ...V + \Delta w ):\, (\psi, V) \in {\bf G}^\diamondsuit (t_i) \}.$$ (3.1)

Проекция на плоскость $x, y$ сечения множества прогноза при фиксированных $u, w$ (аналог (2.8)) теперь на момент $t_{i+1}$ будет иметь вид

$${\bf G}_{\bar\psi, \bar V}(t_{i+1}, u, w) = {\bf G}_{\psi, V}(t_i) + (\Delta V \sin{\psi}, \Delta V \cos{\psi}),$$ (3.2)

где $\bar \psi = \psi + \Delta ku / V$, $\bar V = V + \Delta w$. Перебирая $(\psi, V) \in {\bf G}^\diamondsuit (t_i)$, получим все сечения ${\bf G}_{\bar\psi, \bar V}(t_{i+1}, u, w)$.

Подчеркнем, что при интегрировании по методу Эйлера перенос по формуле (3.2) каждого сечения ${\bf G}_{\psi, V}(t_i)$ определяется только соответствующей парой $(\psi, V)$ и не зависит от $u, w$.

При построении ${\bf G}^\diamondsuit (t_{i+1})$ и ${\bf G}_{\bar\psi, \bar V}(t_{i+1})$ рассматриваем лишь девять вариантов возможных пар управлений:

$${\bf G}^\diamondsuit (t_{i+1}) = \ \bigcup_{u \in \{ -1, 0, 1 \}, \atop w \in \{ \mu_1, 0, \mu_2 \}} {\bf G}^\diamondsuit (t_{i+1}, u, w),$$ (3.3)

$${\bf G}_{\bar\psi, \bar V}(t_{i+1}) = \mbox{\boldmath conv } \bigcup_{u \in \{ -1, 0, 1 \}, \atop w \in \{ \mu_1, 0, \mu_2 \}} {\bf G}_{\bar\psi, \bar V}(t_{i+1}, u, w).$$ (3.4)

Заметим, что ${\bf G}^\diamondsuit (t_{i}) \subset {\bf G}^\diamondsuit (t_{i+1})$.

Множество ${\bf G}^\diamondsuit$ на плоскости $\psi , V$ не является выпуклым и даже может быть несвязно. Поэтому трудно описать его границу. То же самое можно сказать и о множестве ${\bf I}^\diamondsuit$. Будем использовать сетку на плоскости $\psi , V$ с шагом $\delta \psi$ по $\psi$ и с шагом $\delta V$ по $V$. Множества ${\bf G}^\diamondsuit$ и ${\bf I}^\diamondsuit$ будем подменять наборами узлов такой сетки.

В результате пошагового построения множеств прогноза ${\bf G}(t_{i})$ получаем множество ${\bf G}(t^*)$. Согласуя прогноз с замером в момент времени $t^*$ (т.е. с множеством неопределенности $H(t^*)$), находим искомое ИМ: ${\bf I}(t^*) = {\bf G}(t^*) \bigcap H(t^*)$.

3.2 Аппроксимация многоугольниками

На плоскости $x, y$ работаем с выпуклыми множествами ${\bf G}_{\psi, V}$, ${\bf I}_{\psi, V}$ и $H^\char93$. Для их представления будем использовать, применяя аппроксимацию сверху, выпуклые многоугольники. Будем брать на плоскости $x, y$ фиксированный набор векторов (сетка нормалей), на которых будут заданы значения опорной функции многоугольников.

Опишем работу с выпуклыми многоугольниками, заданными на фиксированной сетке векторов. Зафиксируем набор из $m$ единичных векторов $(n_{1},\ldots,n_{m})$ на плоскости $x, y$, расположенных равномерно по углу (с отсчетом от оси $y$ по часовой стрелке):

$$n_{i} = (n_{i_{x}}, n_{i_{y}}) = \left( \sin{ \left(2\pi {... ...}\right) }, \cos{ \left(2\pi {i-1 \over m}\right) } \right).$$ (3.5)

Для любого ограниченного замкнутого множества $D$ на плоскости в качестве аппроксимирующего его сверху будем брать многоугольник $D_{m}$, определяемый наборами значений опорной функции множества $D$ на векторах (3.5): $D_{m} = \{ (x, y)\!\!:\, ( x n_{i_{x}} + y n_{i_{y}}) \le \rho_{i}, \, i = 1, \ldots, m \}$.

При $m = 4$ имеем $4$ вектора, и аппроксимирующий многоугольник есть прямоугольник со сторонами, параллельными осям координат.

3.3 Построение выпуклой оболочки объединения

Пусть многоугольники $A$ и $B$ заданы наборами $( \rho_{1}^{A}, \ldots, \rho_{m}^{A} )$ и $( \rho_{1}^{B}, \ldots, \rho_{m}^{B} )$ значений опорных функций на фиксированной сетке из $m$ векторов (3.5). Выпуклая оболочка $\mbox{\boldmath conv } (A \bigcup B)$ объединения таких многоугольников есть многоугольник, векторы нормалей которого могут не принадлежать сетке $(n_{1},\ldots,n_{m})$. Будем аппроксимировать выпуклую оболочку $\mbox{\boldmath conv } (A \bigcup B)$ многоугольником $C$, который определяется набором $( \rho_{1}^{C}, \ldots, \rho_{m}^{C} )$:

$$\rho_{i}^{C} = \mbox{max}(\rho_{i}^{A}, \rho_{i}^{B}), \quad i = 1, \ldots, m.$$

Многоугольник $C$ является минимальным по включению среди многоугольников, содержащих объединение $A \bigcup B$ и заданных значениями опорной функции на векторах $(n_{1},\ldots,n_{m})$.

Следующая формула определяет оценку сверху возникающей при этом относительной погрешности:

$${ h(C, \mbox{\boldmath conv } (A \bigcup B)) \over \mbox{di... ...1 \over 2} \mbox{\boldmath tg } {\left({\pi \over m} \right)}.$$

На рис. 1 буквой $d$ обозначен диаметр множества $\mbox{\boldmath conv } (A \bigcup B)$, буквой $h$ - хаусдорфово расстояние между $C$ и $\mbox{\boldmath conv } (A \bigcup B)$.

Рис. 1. Погрешность овыпукления при $m=8$.

3.4 Операция пересечения

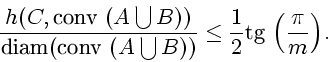
Пересечение многоугольников $A$ и $B$, заданных наборами $( \rho_{1}^{A}, \ldots, \rho_{m}^{A} )$ и $( \rho_{1}^{B}, \ldots, \rho_{m}^{B} )$ значений опорных функций, осуществляется путём вычисления набора $( \rho_{1}, \ldots, \rho_{m} )$

$$\rho_{i} = \mbox{min}(\rho_{i}^{A}, \rho_{i}^{B}), \quad i = 1, \ldots, m,$$

который определяет многоугольник $C = A \bigcap B$ как пересечение полуплоскостей $(x n_{i_{x}} + y n_{i_{y}} ) \le \rho_{i}$, $i = 1, \ldots, m$.

Полученный набор $( \rho_{1}, \ldots, \rho_{m} )$ не обязательно совпадает с набором $( \rho_{1}^{C}, \ldots, \rho_{m}^{C} )$ значений опорной функции многоугольника $C$, вычисленных на заданной фиксированной сетке векторов (3.5). Кроме того, пересечение может быть пусто. Поэтому производится дополнительная обработка набора $( \rho_{1}, \ldots, \rho_{m} )$, состоящая из двух шагов. В результате получаем искомый набор $( \rho_{1}^{C}, \ldots, \rho_{m}^{C} )$ значений опорной функции многоугольника $C$ на заданной фиксированной сетке векторов, либо выясняем, что результат пересечения есть пустое множество.

Шаг 1. Рассматриваем набор $( \rho_{1}, \ldots, \rho_{m} )$ как замкнутый список, в котором $\rho_{1}$ и $\rho_{m}$ считаются соседними. Вычёркиваем из этого списка все элементы $\rho_{i}$, не совпадающие с соответствующими значениями $\rho_{i}^{C}$ опорной функции множества $C = A \bigcap B$. При этом используем следующий критерий.

Пусть $\rho_{i}$, $\rho_{j}$ и $\rho_{k}$ - три последовательных элемента из рассматриваемого списка. Тогда, если

$${n_{k_{y}} ( \rho_{i} n_{j_{x}} - \rho_{j} n_{i_{x}} ) + n_... ...over n_{i_{y}} n_{j_{x}} - n_{i_{x}} n_{j_{y}} } > \rho_{k},$$ (3.6)

то вычёркиваем средний элемент $\rho_{j}$.

Так продолжаем до получения набора, в котором условие (3.6) не выполняется для любой тройки соседних векторов.

Если после очередного вычёркивания некоторого элемента $\rho_{j}$ угол между соседними векторами $n_{i}$ и $n_{k}$ стал больше или равен $\pi$, т.е. если выполнено условие

$$( n_{i_{y}} n_{k_{x}} - n_{i_{x}} n_{k_{y}} ) \le 0,$$ (3.7)

то результат пересечения есть пустое множество, и выполнение операции пересечения завершается. При практической реализации данного алгоритма условие (3.7) необходимо проверять с некоторым запасом.

После первого шага получаем список $\{ \rho_{i}^{C} \}$, каждому элементу которого соответствует сторона многоугольника $C$.

Шаг 2. Список $\{ \rho_{i}^{C} \}$ дополняем недостающими значениями опорной функции на фиксированной сетке $(n_{1},\ldots,n_{m})$ векторов и получаем искомое представление множества $C = A \bigcap B$ в виде набора $( \rho_{1}^{C}, \ldots, \rho_{m}^{C} )$. При этом используем следующий способ дополнения.

Пусть между соседними $\rho_{i}$ и $\rho_{k}$ имеются недостающие значения опорной функции. Вычисляем точку $(x, y)$ пересечения соответствующих соседних сторон. Недостающие промежуточные значения опорной функции далее считаем по формуле

$$\rho_{j} = x n_{j_{x}} + y n_{j_{y}}.$$

В случае $m = 4$ дополнительная обработка (Шаг 1, Шаг 2) набора $( \rho_{1}, \ldots, \rho_{4} )$ сводится лишь к проверке невырожденности пересечения множеств $A$ и $B$ по одновременному выполнению двух неравенств $( \rho_{1} + \rho_{3} ) > 0$ и $( \rho_{2} + \rho_{4} ) > 0$.