2. Схема построения информационных множеств

2.1 Формальное описание информационных множеств

Считаем известным начальное информационное множество $I(t_0)$. Оно формируется на основе предварительных сведений и по множеству неопределенности начального замера.

Пусть в некоторый момент времени $t_*$ информационное множество $I(t_*)$ построено, и следующий замер приходит в момент $t^* > t_*$. Определим множество прогноза $G(t^*)$ как множество достижимости системы (1.1) в момент времени $t^*$ из состояний, принадлежащих множеству $I(t_*)$ в момент $t_*$:

$$G(t^*) = \bigcup_{ u(\cdot), w(\cdot), \atop s \in I(t_*)} \xi(t^*; t_*, s, u(\cdot), w(\cdot)).$$

Здесь $\xi(t^*; t_*, s, u(\cdot), w(\cdot))$ - решение системы дифференциальных уравнений (1.1), доведённое до момента $t^*$, при начальном состоянии $s$ в момент $t_*$ и кусочно-непрерывных управлениях $u(\cdot)$ и $w(\cdot)$.

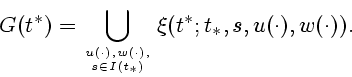
Множество неопределенности несёт новую информацию о системе, поэтому $I(t^*)$ определяется как пересечение множества прогноза $G(t^*)$ и множества неопределённости $H(t^*)$ пришедшего замера:

$$I(t^*) = G(t^*) \bigcap H(t^*).$$ (2.1)

Если в момент $t^*$ замер отсутствует, то операция пересечения не выполняется и полагается, что текущее информационное множество $I(t^*)$ совпадает с текущим множеством прогноза $G(t^*)$. Формально можно считать, что МН отсутствующего замера совпадает со всем пространством $\{ (x, y, \psi, V) \}$.

Таким образом, в каждый текущий момент ИМ определяется начальным множеством $I(t_0)$ и МН замеров, поступивших к этому моменту.

Система (1.1) нелинейна, множество прогноза невыпукло и имеет сложную структуру. Как следствие, достаточно сложно устроено пересечение (2.1). Для эффективного описания ИМ необходимо идти на некоторые упрощения, и мы сделаем их, используя разумным образом специфику системы.

2.2 Эквивалентное представление информационных множеств

Перепишем выражение (2.1), определяющее информационное множество, в удобном для нас эквивалентном виде.

Рассмотрим проекцию $I^\diamondsuit (t_*)$ множества $I(t_*)$ на плоскость $\psi , V$. Каждой точке $(\psi, V) \in I^\diamondsuit (t_*)$ поставим в соответствие сечение $I_{ \psi, V}(t_*)$ информационного множества $I(t_*)$ плоскостью $\{ \psi = \mbox{const}, V = \mbox{const}\}$. Такие сечения будем рассматривать в проекции на плоскость $x, y$:

$$I_{ \psi, V}(t_*) = \left \{ (x, y):\, (x, y, \psi, V) \in I(t_*) \right\}.$$

Информационное множество $I(t_*)$ представим проекцией $I^\diamondsuit (t_*)$ на
плоскость $\psi , V$ и множествами $I_{ \psi, V}(t_*)$ на плоскости $x, y$:

$$I(t_*) = \bigcup_{(\psi, V) \in I^\diamondsuit (t_*)} \left [ I_{ \psi, V}(t_*) \times (\psi, V) \right ].$$ (2.2)

Аналогично запишем множество прогноза

$$G(t^*) = \bigcup_{(\bar\psi, \bar V) \in G^\diamondsuit (t^*)} \left [ G_{ \bar\psi, \bar V}(t^*) \times (\bar\psi, \bar V) \right ].$$ (2.3)

С учетом (1.2), (2.3) формулу (2.1) можно переписать следующим образом:

$$I(t^*) = \bigcup_{(\bar\psi, \bar V) \in G^\diamondsuit (t^*)} \l... ...\psi, \bar V}(t^*) \bigcap H^\char93 (t^*)) \times (\bar\psi, \bar V) \right ].$$ (2.4)

Выражение (2.4) записано в таком же виде, что и (2.2). Это следует из того, что

$$I_{ \bar\psi, \bar V}(t^*) = G_{ \bar\psi, \bar V}(t^*) \bigcap H^\char93 (t^*) ,$$

$$I^\diamondsuit (t^*) = \left \{ (\bar\psi, \bar V) \in G^\d... ...bar\psi, \bar V}(t^*) \bigcap H^\char93 (t^*) \ne \O\right \}.$$

Представление множеств $I(t_*)$, $G(t^*)$, $I(t^*)$ в виде (2.2), (2.3), (2.4) позволяет в дальнейшем перейти к сетке на плоскости $\psi , V$ и рассматривать только те сечения, которые соответствуют узлам сетки.

2.3 Особенности динамики движения

Покажем, что в нашей задаче множества $G^\diamondsuit (t^*)$ и $G_{ \bar\psi, \bar V}(t^*)$ можно вычислять непосредственно на основе множеств $I^\diamondsuit (t_*)$ и $I_{ \psi, V}(t_*)$.

Зафиксируем пару управлений $u(\cdot)$, $w(\cdot)$ на интервале $[t_*, t^*)$. Рассмотрим множество прогноза $G(t^*, u(\cdot), w(\cdot))$ при начальном множестве $I(t_*)$ и управлениях $u(\cdot)$, $w(\cdot)$. Данное множество, как и множество $G(t^*)$, будем представлять проекцией $G^\diamondsuit (t^*, u(\cdot), w(\cdot))$ на плоскость $\psi , V$ и сечениями $G_{\bar\psi, \bar V}(t^*, u(\cdot), w(\cdot))$.

Специфика динамики (1.1) состоит в том, что третье и четвертое уравнения можно интегрировать независимо от первых двух:

$$V(t) = V(t_*) + \int \limits_{t_*}^{t}w (\tau) \,d\tau, \qquad \psi(t) = \psi(t_*) + \int \limits_{t_*}^{t} { ku(\tau) \over V(\tau)} \,d\tau.$$ (2.5)

Следовательно,

$$G^\diamondsuit (t^*, u(\cdot), w(\cdot)) =$$

$$= \left \{ \left (\psi + \displaystyle \int \limits_{t_*}^{t^*} {... ...{t^*}w(t) \,dt \right ) \!\! : \, (\psi, V) \in I^\diamondsuit (t_*) \right \}.$$ (2.6)

Зафиксируем точку $(\psi, V) \in I^\diamondsuit (t_*)$. Фазовые координаты $x, y$ отсутствуют в правой части системы (1.1), поэтому интегрирование первых двух уравнений для начальных состояний из $I_{ \psi, V}(t_*)$ означает перенос на один и тот же вектор. Полагая

$$\bar \psi = \psi(t^*), \quad \bar V = V(t^*),$$ (2.7)

имеем

$$G_{\bar\psi, \bar V}(t^*, u(\cdot), w(\cdot)) =$$

$$= I_{\psi, V}(t_*) + \left (\,\, \displaystyle \int \limits_{t_*}... ...\,dt, \, \displaystyle \int \limits_{t_*}^{t^*}V(t) \cos{\psi(t)}\,dt \right ).$$ (2.8)

Перебирая $(\psi, V) \in I^\diamondsuit (t_*)$, получим все сечения $G_{\bar\psi, \bar V}(t^*, u(\cdot), w(\cdot))$ множества прогноза $G(t^*, u(\cdot), w(\cdot))$.

Будем формально считать, что сечения $G_{\bar\psi, \bar V}(t^*, u(\cdot), w(\cdot))$ заданы для произвольных $(\bar \psi, \bar V)$. Если $(\bar \psi, \bar V) \in G^\diamondsuit (t^*, u(\cdot), w(\cdot))$, т.е. $(\bar \psi, \bar V)$ соответствует некоторой паре $(\psi, V) \in I^\diamondsuit (t_*)$ в силу (2.5), (2.7), то сечение определяется формулой (2.8); иначе $G_{\bar\psi, \bar V}(t^*, u(\cdot), w(\cdot)) = \O$.

В целом, множество $G^\diamondsuit (t^*)$ есть множество достижимости в силу третьего и четвертого уравнений системы (1.1) при начальном множестве $I^\diamondsuit (t_*)$:

$$G^\diamondsuit (t^*) = \bigcup_{u(\cdot), w(\cdot)} G^\diamondsuit (t^*, u(\cdot), w(\cdot)).$$ (2.9)

Множества $G_{ \bar\psi, \bar V}(t^*)$ вычисляются по формуле

$$G_{\bar\psi, \bar V}(t^*) = \bigcup_{u(\cdot), w(\cdot)}G_{\bar\psi, \bar V}(t^*, u(\cdot), w(\cdot)).$$ (2.10)

2.4 Овыпукление сечений

При нахождении множеств $G_{ \bar\psi, \bar V}(t^*)$ имеем дело с объединением (2.10) множеств на плоскости $x, y$. Множества $G_{ \bar\psi, \bar V}(t^*)$ пересекаются затем с множеством $H^\char93 (t^*)$. Трудность состоит в том, что множества $G_{ \bar\psi, \bar V}(t^*)$ невыпуклы.

Условимся подменять множества $G_{ \bar\psi, \bar V}(t^*)$ их выпуклыми оболочками. Таким образом, одновременно с операцией (2.10) объединения множеств $G_{\bar\psi, \bar V}(t^*, u(\cdot), w(\cdot))$, вычисляем выпуклую оболочку. Получаем множество ${\bf G}_{\bar\psi, \bar V}(t^*) = \mbox{\boldmath conv } G_{ \bar\psi, \bar V}(t^*)$. Положим

$${\bf G}(t^*) = \bigcup_{(\bar\psi, \bar V) \in G^\diamondsuit (t^*)} \left [{\bf G}_{\bar\psi, \bar V}(t^*) \times (\bar\psi, \bar V)\right ],$$ (2.11)

$${\bf I}(t^*) = \bigcup_{(\bar\psi, \bar V) \in G^\diamondsuit (t^*)} \left [ ( {... ...psi, \bar V}(t^*) \bigcap H^\char93 (t^*) ) \times (\bar\psi, \bar V)\right ].$$ (2.12)

Формулы (2.11), (2.12) написаны для момента $t^*$ в предположении о применении операции овыпукления только на промежутке $[t_*, t^*]$. Имеем $G(t^*) \subset {\bf G}(t^*)$ и $I(t^*) \subset {\bf I}(t^*)$.

Если овыпукление проводить с начального момента $t_0$, то на момент $t_*$ будем иметь ${\bf I}(t_*)$ с выпуклыми сечениями ${\bf I}_{\psi, V}(t_*)$. Поэтому при нахождении множества ${\bf G}_{\bar\psi, \bar V}(t^*)$ будем строить выпуклую оболочку объединения выпуклых множеств.

Далее речь пойдет о построении множеств ${\bf G}$ и ${\bf I}$. Будем по-прежнему называть их множеством прогноза и информационным множеством.