3. Стабильность стохастического программного максимина.

Обсудим свойства величины $e(\cdot)$. Пусть реализовалась история
$w[t_0[\cdot]\tau_*]$, $\tau_* \in [t_0,\vartheta)$. Положим $\tau^*=\tau_2\in \Delta_k\{\tau_j\}$. Разбиение $\Delta_k\{\tau_j\}$ (2.2) выбрано так, что из определений (2.6) и (2.8) вытекают равенства

$$g_{\alpha}(\tau^*)=h_{\alpha}(\tau_*)+1,\qquad \alpha=1,2,$$ (3.1)

и возможны три случая.

В первом случае, когда $g_1(\tau^*)=g_1(\tau_*)$, $g_2(\tau^*)=g_2(\tau_*)$, момент $\tau_*$ не совпадает ни с одним из моментов разбиений $\Delta_{t_{\alpha}^{[i_{\alpha}]}}$ (1.2), $\alpha=1,2$.

Во втором случае, когда $g_1(\tau^*)=g_1(\tau_*)+1$, $g_2(\tau^*)=g_2(\tau_*)$, имеем $\tau_*=t^{[g_1(\tau_*)]}$.

В третьем случае, когда $g_2(\tau^*)=g_2(\tau_*)+1$, $g_1(\tau^*)=g_1(\tau_*)$, получаем $\tau_*=t^{[g_2(\tau_*)]}$.

Пусть $w[t_0[\cdot]\tau^*]$ - история, а $\{\tau^*,w^*=w[\tau^*]\}$ - позиция, полученные к моменту $\tau=\tau^*$ на некотором движении $w[\tau]$, $\tau_* \leq \tau \leq \tau^*$ модели (2.1) под воздействием пары допустимых детерминированных управлений $u[\tau]\in P$, $v[\tau]\in Q$, $\tau_* \leq \tau \leq \tau^*$. Для отрезка $[\tau^*,\vartheta]$ назначим разбиение $\Delta_{k^*}^{*}\{\tau_{p}^{*}\}$, $\tau_{1}^{*}=\tau^*,\ldots,\tau^*_{k^*+1}=\vartheta$, так что $\tau_{p}^*=\tau_j$, $p=j-1$, $p=1,\ldots,k^*$; $k^*=k-1$ (в случае $\tau^*=\vartheta$ символом $\Delta_{k^*}^{*}\{\tau_{p}^{*}\}$ обозначим множество, состоящее из одной точки $\{\tau_{1}^*=\tau^{*}=\vartheta\}$). Запишем величину $e(w[t_0[\cdot]\tau^*],\Delta_{k^*}^{*}\{\tau_{p}^{*}\})$. По определению (2.11) этой величины, имеем

$$\begin{array}{c} \displaystyle e(w[t_0[\cdot]\tau^*],\Delta_... ...{\bf l}^*(\cdot)),\\ [3ex] t_0\leq\tau^*<\vartheta, \end{array}$$ (3.2)

Здесь $\omega^*=\{\xi_1^*,...,\xi_{k^*}^*\}$ - элементарное событие из вероятностного пространства $\{\Omega^*,B^*,$P$^*$$\}$; $\xi_p^* \in [0,1]$ - равномерно распределенные случайные величины, связанные с моментами $\tau_p^*$, $p=1,\ldots,k^*$, $k^*=k-1$; $\Omega^*=\{\omega^*\}$ - единичный куб в $k^*$-мерном пространстве, $B^*$ - борелевская $\sigma$-алгебра для этого куба, P$^*=$P$^*$(B$^*$) - мера Лебега; ${\bf l}^*(\cdot)\in {\bf L}^{\infty}(\Omega^*)$.

Справедливо следующее утверждение об $u$-стабильности величины
$e(\cdot)$ (2.11).

Лемма 3.1   Пусть реализовалась история $w[t_0[\cdot]\tau_*]$, $\tau_* \in [t_0,\vartheta)$ движения системы $(\ref{2.1})$ и назначено разбиение $\Delta_k$ $(2.2)$ отрезка $[\tau_*,\vartheta]$. Тогда для всякой допустимой реализации $v_*[\tau_*[\cdot]\tau^*)=\{v_*[\tau] \in Q,\quad \tau_*\leq \tau< \tau^*\}$, где $\tau^*=\tau_2\in \Delta_k$, найдется такая допустимая реализация $u[\tau_*[\cdot]\tau^*)=\{u[\tau] \in P,\quad \tau_*\leq \tau< \tau^*\}$, что под действием этих управлений реализуется история $w[t_0[\cdot]\tau^*]$, для которой будет справедливо неравенство

$$e(w[t_0[\cdot]\tau^*],\Delta_{k^*}^{*})-e(w[t_0[\cdot]\tau_*],\Delta_k)\leq0.$$ (3.3)

На возможных реализациях $w[t_0[\cdot]\tau^*]$ рассмотрим вспомогательную величину

$${\hat e}(w[t_0[\cdot]\tau_*],\tau^*,w[\tau^*],\Delta_{k^*}^{*}\{\tau_{p}^{*}\})=\mbox{}$$

$$\mbox{}= \sup_{\Vert {\bf l}^*(\cdot)\Vert^* \le 1} {\hat \c... ...\{\tau_{p}^{*}\},{\bf l}^*(\cdot)),~ t_0\leq\tau^*<\vartheta,$$ (3.4)

где

$${\hat \chi}(w[t_0[\cdot]\tau_*],\tau^*,w[\tau^*],\Delta_{k^*... ...)= {\hat \sigma}(w[t_0[\cdot]\tau_*],{\bf l^*}(\cdot))+\mbox{}$$

$$\mbox{}+\langle m_{(\tau^*)}({\bf l}^*(\cdot)),X[\vartheta,\tau^*]w[\tau^*] \rangle+\mbox{}$$

$$\mbox{}+ M\{\sum_{p=1}^{k^*}\Delta \psi_p(\tau_*;m^{(\tau_p^*)}({\bf l}^*(\cdot);\xi_1^*,\ldots,\xi_p^*))\},$$ (3.5)

$${\hat \sigma}(w[t_0[\cdot]\tau_*],{\bf l^*}(\cdot))= \sum_{i... ...langle M\{l_1^{*[i_1]}(\omega)\},w[t_1^{[i_1]}]\rangle+\mbox{}$$

$$\mbox{}+ \sum_{i_2=1}^{h_2(\tau_*)}\langle M\{l_2^{*[i_2]}(\omega)\},w[t_2^{[i_2]}]\rangle.$$ (3.6)

Непосредственно из (3.1), (3.2) и (3.4)-(3.6) получаем равенство

$${\hat e}(w[t_0[\cdot]\tau_*],\tau^*,w[\tau^*],\Delta_{k^*}^{*}) =e(w[t_0[\cdot]\tau^*],\Delta_{k^*}^{*})$$ (3.7)

какая бы история $w[t_0[\cdot]\tau^*]$ ни реализовалась.

Пусть $W=W(\tau^*;\tau_*,w[\tau_*],v_*[\tau_*[\cdot]\tau^*))$ - область достижимости к моменту времени $\tau^*$ для движений $w[\tau_*[\cdot]\tau^*]$ порожденных фиксированным управлением $v_*[\tau_*[\cdot]\tau^*)$ и различными допустимыми $u[\tau_*[\cdot]\tau^*)$ с ним в паре. Это множество будет непустым выпуклым компактом в $R^n$. Рассмотрим также множество

$$G=\{({\bf k}^*,m^*):~({\bf k}^*,m^*)=(\{l^{*[1]}_{1},\ldots,... ...u_*)]}_{1}, l^{*[1]}_{2},\ldots,l^{*[h_2(\tau_*)]}_{2}\},m^*),$$

$$~m^*=\sum_{i_1=g_1(\tau^*)}^{N_1}X^T[t_1^{[i_1]},\vartheta]l... ..._{i_2=g_2(\tau^*)}^{N_2}X^T[t_2^{[i_2]},\vartheta]l_2^{[i_2]},$$

$$\mu_1^{*[i_1]}(l_1^{[i_1]})\leq 1, \ i=1,\ldots,N_1, \ \sum_{i_2=1}^{N_2}\mu_2^{*[i_2]}(l_2^{[i_2]})\leq 1\},$$ (3.8)

которое является непустым выпуклым компактом в $R^{n \cdot (h_1(\tau_*)+h_2(\tau_*)+1)}.$
Здесь символами $l_{\alpha}^{[i_{\alpha}]}$ обозначены детерминированные $n$-мерные векторы. Далее покажем, что при фиксированной истории $w[t_0[\cdot]\tau_*]$ найдется пара $\{({\bf k}^*_0,m^*_0),w^*_0\}$, $({\bf k}^*_0,m^*_0)\in G$, $w^*_0\in W$, удовлетворяющая следующим двум условиям.

$(i)$ Существует последовательность случайных величин $\{{\bf l}^*_{(s)}(\cdot),$
$s=1,2,\ldots\}$, ${\bf l}^*_{(s)}(\cdot)\in {\bf L}^{(\infty)}(\Omega^*)$, $\Vert {\bf l}^*_{(s)}(\cdot)\Vert^*\leq 1$, для которой выполняется равенство

$${\hat e}(w[t_0[\cdot]\tau_*],\tau^*,w^*_0,\Delta_{k^*}^{*}) ... ...\tau_*],\tau^*,w^*_0,\Delta_{k^*}^{*}, {\bf l}^*_{(s)}(\cdot))$$ (3.9)

и для которой существуют пределы

$$\begin{array}{c} \displaystyle {\bf k}^*_0=\lim_{s\to\infty}... ...quad m^{*(s)}=m_{(\tau^*)}({\bf l}^*_{(s)}(\cdot)). \end{array}$$ (3.10)

$(ii)$ Выполняется равенство

$$\langle m^*_0,X[\vartheta,\tau^*]w^*_0\rangle =\min_{w \in W}\langle m^*_0,X[\vartheta,\tau^*]w\rangle.$$ (3.11)

Действительно, построим отображение из $D=G\times W$ в $D$. Каждому вектору $w^* \in W$ поставим в соответствие множество $G^0(w^*)\subset G$ (3.8) всех возможных векторов $({\bf k}^*_0,m^*_0)$ , удовлетворяющих $(i)$ при $w^*_0=w^*$. Можно показать, что множество $G^0(w^*)$ является непустым выпуклым компактом в $R^{n \cdot (h_1(\tau_*)+h_2(\tau_*))}$ и отображение $w^* \to G^0(w^*)$ полунепрерывно сверху по включению. Каждому $({\bf k}^*,m^*)\in G$ поставим в соответствие множество $W^0({\bf k}^*,m^*)=W^0(m^*)\subset W$ всех векторов $w^*_0$, удовлетворяющих условию $(ii)$, при замене в (3.11) $m^*_0$ на $m^*$. Множество $W^0({\bf k}^*,m^*)$ - непустой выпуклый компакт в $R^n$ и отображение $({\bf k}^*,m^*) \to W^0({\bf k}^*,m^*)$ полунепрерывно сверху по включению. Таким образом каждой паре $\{({\bf k}^*,m^*),w^*\}\in D$ соответствует множество $R[({\bf k}^*,m^*),w^*]\subset D$ пар $\{ ({\bf k}^*_{(1)},m^*_{(1)}),w^*_{(1)}\}$, $({\bf k}^*_{(1)},m^*_{(1)})\in G^0(w^*)$, $w^*_{(1)}\in W^0({\bf k}^*,m^*)$. В силу теоремы Какутани (см. [11, стр. 638]), построенное отображение имеет неподвижную точку $\{({\bf k}^*_0,m^*_0),w^*_0\}\in D$, для которой выполнены условия $(i)$-$(ii)$.

Пусть $u^0[\tau_*[\cdot]\tau^*)$ - то допустимое управление, которое в паре с $v_*[\tau_*[\cdot]\tau^*)$ приводит в точку $w_0^*=w_0[\tau^*]$, т.е.

$$w_0^*=X[\tau^*,\tau_*]w[\tau_*] + \int \limits_{\tau_*}^{\tau^*} X[\tau^*,\tau](B(\tau)u^0[\tau]+C(\tau)v_*[\tau])d\tau.$$ (3.12)

При этом реализуется история $w_0[t_0[\cdot]\tau^*]$. Тогда из (3.11), снова учитывая формулу Коши и определение области достижимости $W$, а также возможность внесения здесь знака минимума под знак интеграла, получаем равенство

$$\int \limits_{\tau_*}^{\tau^*} \langle m^*_0, X[\vartheta,\t... ... \in P}\langle m^*_0, X[\vartheta,\tau]B(\tau)u \rangle d\tau.$$ (3.13)

Максимизирующей последовательности $\{{\bf l}^*_{(s)}(\cdot),s=1,2,\ldots\}$ (которая, согласно $(i)$, отвечает вектору $w^*_0$), поставим в соответствие последовательность случайных векторных величин $\{{\bf\hat l}_{(s)}(\cdot),s=1,2,\ldots\}$:

$${\bf\hat l}_{(s)}(\cdot)=\{ \{\hat l_{1,(s)}^{[1]}(\omega),\... ...(\omega)\}, ~\omega\in \Omega\}\in {\bf L}^{(\infty)}(\Omega),$$

$$\hat l_{\alpha,(s)}^{[i_{\alpha}]}(\omega)= l_{\alpha,(s)}^{... ...pha}=1,\ldots,N_{\alpha},\ \ \ \alpha=1,2,\ \ \ s=1,2,\ldots\,$$ (3.14)

где случайные величины $\xi_1^*,...,\xi_{k^*}^*$ из набора $\{\xi_1^*,...,\xi_{k^*}^*\}=\omega^*$ трактуются как компоненты $\xi_2,\ldots,\xi_k$ из набора $\{\xi_1,\ldots,\xi_k\}=\omega$, т.е в (3.14) полагаем

$$\xi_{p}^*=\xi_{p+1},\quad p=1,\ldots,k^*.$$ (3.15)

Заметим, что $\Vert \hat {\bf l}_{(s)}(\cdot) \Vert\leq 1$. Из (2.9), (2.10) и (3.14) c учетом (2.6), (2.8) для каждого $s=1,2,\ldots$ получаем равенства

$$\begin{array}{c} M\{\hat l_{\alpha,(s)}^{[i_{\alpha}]}(\omeg... ...(\tau_*)-1,\qquad \alpha=1,2, \qquad s=1,2,\ldots\, \end{array}$$ (3.16)

$$m_{(\tau_*)}({\bf\hat l}_{(s)}(\cdot)) =\left\{ \begin{array... ...(s)}, & \tau_*= t_{2}^{[g_{2}(\tau_*)]}, \end{array} \right.$$ (3.17)

$$m^{(\tau_1)}({\bf\hat l}_{(s)}(\cdot);\xi_1)=m^{*(s)},$$ (3.18)

$$m^{(\tau_j)}({\bf\hat l}_{(s)}(\cdot);\xi_1,...,\xi_j)= m^{(... ...l}^*_{(s)}(\cdot);\xi_1^*,...,\xi_{j-1}^*),\quad j=2,\ldots,k,$$ (3.19)

где, как и в (3.14), подразумевается выполненным условие (3.15).

Далее из (2.13), (3.1), (3.6) и (3.16) получаем равенства

$${\sigma(w[t_0[\cdot]\tau_*]),{\bf\hat l}_{(s)}(\cdot))=}$$

$$= \left\{ \begin{array}{ll} {\hat \sigma}(w[t_0[\cdot]\tau_*]),{\bf... ... &\mbox{при}\ \ \ \tau_*= t_{2}^{[g_{2}(\tau_*)]},\\ [3ex] \end{array} \right.$$ (3.20)

Рассмотрим первый случай, когда $\tau_*\neq t_{\alpha}^{[g_{\alpha}(\tau_*)]}$, $\alpha=1,2$. Учитывая определения $e(w[t_0[\cdot]\tau_*],\Delta_k)$ (2.11) и $\{{\bf\hat l}_{(s)}(\cdot),~s=1,2,\ldots\}$ (3.14), а также правило взятия повторных математических ожиданий и соотношения (3.15)-(3.20), для любого номера $s=1,2,\ldots$ получаем следующую цепочку соотношений:

$$e(w[t_0[\cdot]\tau_*],\Delta_k) \ge \chi(w[t_0[\cdot]\tau_*]... ...t \sigma}(w[t_0[\cdot]\tau_*]),{\bf l}^*_{(s)}(\cdot))+\mbox{}$$

$$\mbox{}+\langle m^{*(s)},X[\vartheta,\tau_*]w_* \rangle+ \Delta \psi_1(\tau_*;m^{*(s)})+\mbox{}$$

$$\mbox{}+ M\{\sum_{p=1}^{k^*}\Delta \psi_p(\tau_*;m^{(\tau_p^*)}({\bf l}^*_{(s)}(\cdot); \xi_1^*,\ldots,\xi_p^*))\}.$$ (3.21)

С другой стороны, по определению $e(w_0[t_0[\cdot]\tau^*],\Delta_{k^*}^{*})$ и $\{{\bf l}_{(s)}^*(\cdot),~s=1,2,\ldots\}$ в согласии с (3.4)-(3.7) и (3.10) для любого номера $s=1,2,\ldots$ имеем

$$e(w_0[t_0[\cdot]\tau^*],\Delta_{k^*}^{*})= {\hat e}(w[t_0[\cdot]\tau_*],\tau^*,w_0^*,\Delta_{k^*}^{*})\le \mbox{}$$

$$\mbox{} \le {\hat \chi}(w_0[t_0[\cdot]\tau_*],\tau^*,w_0^*,\Delta_{k^*}^{*},{\bf l}^*_{(s)}(\cdot)) +\varepsilon_s= \mbox{}$$

$$\mbox{}= {\hat \sigma}(w[t_0[\cdot]\tau_*],{\bf l}^*_{(s)}(\... ...))+ \langle m^{*(s)},X[\vartheta,\tau^*]w_0^* \rangle+ \mbox{}$$

$$\mbox{}+ M \left\{\sum_{p=1}^{k^*}\Delta \psi_p(\tau_*;m^{(\... ...*_{(s)}(\cdot);\xi_1^*,\ldots,\xi_p^*))\right\}+\varepsilon_s,$$ (3.22)

где $\varepsilon_s>0 \quad (s=1,2,\ldots)$ и $\lim \limits_{s\to \infty}\varepsilon_s=0$. Из (3.21) и (3.22) для любого номера s=1,2,... получаем неравенство

$$e(w_0[t_0[\cdot]\tau^*],\Delta_{k^*}^{*})-\varepsilon_s- e(w[t_0[\cdot]\tau_*],\Delta_k)\leq \mbox{}$$

$$\mbox{} \leq \langle m^{*(s)},X[\vartheta,\tau^*]w^*_0 \rang... ...X[\vartheta,\tau_*]w_* \rangle-\Delta \psi_1(\tau_*;m^{*(s)}).$$ (3.23)

При этом в силу условия $(i)$ соответствующая последовательность $\{m^{*(s)},$
$s=1,2,\ldots\}$ (3.10) сходится к $m^*_0$. Предельным переходом в (3.23) при $s \to \infty$, используя (3.12), получаем оценку

$$e(w_0[t_0[\cdot]\tau^*],\Delta_{k^*}^{*})- e(w[t_0[\cdot]\tau_*],\Delta_k)\leq$$

$$\mbox{} \leq \int \limits_{\tau_*}^{\tau^*} \langle m^*_0,B(... ...}^{\tau^*} \min_{u \in P}\langle m^*_0, B(\tau)u\rangle d\tau,$$

которая в силу (3.13), дает неравенство (3.3).

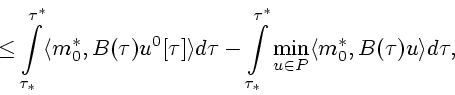
Пусть теперь $\tau_*=t^{[g_{\alpha}(\tau_*)]}$, где $\alpha=1$ или $\alpha=2$. В этом случае из (2.11), (3.14), опираясь на (3.16)-(3.20), получаем оценку

$$e(w[t_0[\cdot]\tau_*],\Delta_k) \ge \chi(w[t_0[\cdot]\tau_*],\Delta_k,{\bf\hat l}_{(s)}(\cdot))=\mbox{}$$

$$\mbox{}= {\hat \sigma}(w[t_0[\cdot]\tau_*]),{\bf l}^*_{(s)}(... ...^{*[g_{\alpha}(\tau_*)]}(\omega^*)\},w[\tau_*]\right> +\mbox{}$$

$$\langle X^T[\tau_*,\vartheta]M\{l_{\alpha,(s)}^{*[g_{\alpha}... ...au_*]w[\tau_*] \rangle+ \Delta \psi_1(\tau_*;m^{*(s)})+\mbox{}$$

$$\mbox{}+ M\{\sum_{p=1}^{k^*}\Delta \psi_p(\tau_*;m^{(\tau_p^*)}({\bf l}^*_{(s)}(\cdot); \xi_1^*,\ldots,\xi_p^*))\}.$$ (3.24)

Здесь $\alpha=1$, если $\tau_*=t_1^{[g_1(\tau_*)]}$ или $\alpha=2$, если $\tau_*=t_2^{[g_2(\tau_*)]}$.

Таким образом, из (3.24) снова имеем (3.21). Рассуждая далее как в первом случае, при учете (3.21)-(3.23) получим (3.3). Итак, лемма 3.1 доказана.