| (4.1) |
![\begin{displaymath}
m({\bf q}_{[j]}(\cdot))=\sum_{i_1=h_1(\tau_j)+1}^{N_1}X^{T}[t_1^{[i_1]},
\vartheta]M\{q_{[j],1}^{[i_1]}(\omega)\}+ \mbox{}
\end{displaymath}](img325.gif)
![\begin{displaymath}
\mbox{}+
\sum_{i_2=h_2(\tau_j)+1}^{N_2}X^{T}[t_2^{[i_2]},\vartheta]M\{q_{[j],2}^{[i_2]}(\omega)\}.
\end{displaymath}](img326.gif)
![\begin{displaymath}
\mbox{}=
\sum_{i_1=h_1(\tau_p)+1}^{N_1}X^T[t_1^{[i_1]},\vart...
...]}_{[j],1}(\xi_j,\ldots,\xi_k)\mid\xi_j,\ldots,\xi_p\}+\mbox{}
\end{displaymath}](img332.gif)
![\begin{displaymath}
\mbox{}+
\sum_{i_2=h_2(\tau_p)+1}^{N_2}X^T[t_2^{[i_2]},\vart...
..._j,\ldots,\xi_k)\mid\xi_j,\ldots,\xi_p\},
\quad j\leq p\leq k.
\end{displaymath}](img333.gif)
Отметим, что из (2.8)-(2.13), (4.5) (при ![]() )
и определения области
)
и определения области
![]() (4.4) следует равенство
(4.4) следует равенство
![\begin{displaymath}
e(x[t_0[\cdot]t_*],\Delta_k)=\sum_{i_1=1}^{h_1(t_*)}\mu_1^{[i_1]}(x[t_1^{[i_1]}])+
\mbox{}
\end{displaymath}](img336.gif)
![\begin{displaymath}
\mbox{} +
\sup_{(m_{(1)},\nu_{(1)}) \in G_1(t_*)}
[(1-\nu_{(...
...1\leq i_2 \leq h_2(t_*)}\mu_2^{[i_2]}(x[t_2^{[i_2]}])+
\mbox{}
\end{displaymath}](img337.gif)
Таким образом, для вычисления величины
![]() (2.11)
требуется решить задачу поиска точной верхней грани функционала
(2.11)
требуется решить задачу поиска точной верхней грани функционала
![]() на множестве случайных вектор-функций
на множестве случайных вектор-функций
![]() :
:
![]() ,
,
![]() .
Далее будет показано, что решение этой задачи приведет к известной процедуре
([10]) построения выпуклых сверху оболочек для вспомогательных
функций из детерминированной программной конструкции. Приведем здесь эту конструкцию.
Следуя [10], определим рекуррентную
последовательность функций
.
Далее будет показано, что решение этой задачи приведет к известной процедуре
([10]) построения выпуклых сверху оболочек для вспомогательных
функций из детерминированной программной конструкции. Приведем здесь эту конструкцию.
Следуя [10], определим рекуррентную
последовательность функций
![]() ,
,
![]() .
При
.
При ![]() полагаем
полагаем
Докажем далее, что справедливо равенство
1)
![]() ;
;
2)![]() имеют лебегову меру
имеют лебегову меру
![]() ,
,
![]() .
.
Определим теперь рекуррентную последовательность величин
В случае, когда
![]() ,
,
![]() ,
полагаем
,
полагаем
В случае, когда
![]() ,
,
![]() ,
сначала каждому фиксированному вектору
,
сначала каждому фиксированному вектору
![]() произвольным выбором поставим в соответствие пару векторов
произвольным выбором поставим в соответствие пару векторов
![]() ,
,
![]() ,
,
![]() ,
,
![]() , решающих задачу на
максимум в (4.11) при условии (4.12), если в
(4.11), (4.12) положить
, решающих задачу на
максимум в (4.11) при условии (4.12), если в
(4.11), (4.12) положить
![]() ,
,
![]() . Затем определяем
. Затем определяем
Продолжая индукцию до ![]() , получим
, получим
![]() ,
,
![]() ,
,
![]() ,
, ![]() . Построенные функции
. Построенные функции
![]() конечнозначны по
конечнозначны по
![]() при каждом
при каждом
![]() . Можно проверить, что они
удовлетворяют условиям (4.1)-(4.3), так что
. Можно проверить, что они
удовлетворяют условиям (4.1)-(4.3), так что
![]() ,
, ![]() . Покажем, что они также
обладают следующими свойствами.
. Покажем, что они также
обладают следующими свойствами.
![]() . Для любого вектора
. Для любого вектора
![]() выполняются равенства
выполняются равенства
![]() . Для любого вектора
. Для любого вектора
![]() , для любых
, для любых
![]() таких, что
таких, что
![]() ,
,
![]() ,
,
![]() выполняется неравенство
выполняется неравенство
Доказательство свойств ![]() и
и ![]() ,
, ![]() проведем по индукции. Пусть
проведем по индукции. Пусть ![]() . Свойство
. Свойство ![]() вытекает непосредственно из определения
вытекает непосредственно из определения
![]() (4.5), построения
(4.5), построения
![]() (4.17),
(4.18), если учесть (4.16) при
(4.17),
(4.18), если учесть (4.16) при ![]() . Проверим, что выполняется свойство
. Проверим, что выполняется свойство
![]() . Возьмем любую допустимую
. Возьмем любую допустимую
![]() .
Она определена на вероятностном пространстве
.
Она определена на вероятностном пространстве
![]() P
P![]() ,
где
,
где
![]() - единичный отрезок,
- единичный отрезок, ![]() - борелевская
- борелевская
![]() -алгебра на этом отрезке, P
-алгебра на этом отрезке, P![]() - мера Лебега.
Рассмотрим также вероятностное пространство
- мера Лебега.
Рассмотрим также вероятностное пространство
![]() P
P
![]() ,
где
,
где
![]() ,
,
![]() - борелевская
- борелевская ![]() -алгебра на
-алгебра на
![]() ,
P
,
P
![]() - мера Лебега. Применяя теорему о замене переменных
под знаком интеграла Лебега
(см. [14, стр. 213]), из вогнутости
- мера Лебега. Применяя теорему о замене переменных
под знаком интеграла Лебега
(см. [14, стр. 213]), из вогнутости
![]() ,
,
![]() , неравенства Иенсена (см. [14, стр. 209]),
а также неравенства
, неравенства Иенсена (см. [14, стр. 209]),
а также неравенства
![]() ,
,
![]() получаем, что существует мера
получаем, что существует мера
![]() для которой
для которой
![\begin{displaymath}
\int \limits_{[\xi_k]}
\{q_{[k],\alpha}^{[N_{\alpha}]}(\xi_k),q_{[k],0}(\xi_k)\}d\xi_k
=\end{displaymath}](img452.gif)
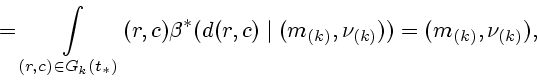
![\begin{displaymath}
g_k(t_*;{\bf q}_{[k]}(\cdot))=\int \limits_{[\xi_k]}\psi_k(t_*;
q^{[N_{\alpha}]}_{[k],\alpha}(\xi_k),q_{[k],0}(\xi_k))d\xi_k=
\end{displaymath}](img454.gif)
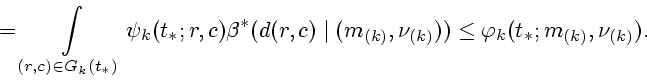
Предположим теперь, что при ![]() (
(![]() ) выполняются свойства
) выполняются свойства
![]() и
и ![]() . Покажем, что тогда имеют место свойства
. Покажем, что тогда имеют место свойства
![]() и
и ![]() для
для
![]() ,
,
![]() .
Доказательство приведем здесь для наиболее сложного
случая, когда
.
Доказательство приведем здесь для наиболее сложного
случая, когда
![]() ,
,
![]() .
Свойство
.
Свойство ![]() вытекает из построения (4.17), (4.26), (4.25) если
в выражениях, определяющих
вытекает из построения (4.17), (4.26), (4.25) если
в выражениях, определяющих
![]() ,
,
![]() и
и
![]() (см. (4.5)),
перейти от от интегрирования по области
(см. (4.5)),
перейти от от интегрирования по области
![]() к повторному интегрированию
(см. [14, стр. 215]) сначала по
области
к повторному интегрированию
(см. [14, стр. 215]) сначала по
области
![]() , а потом по
, а потом по ![]() и далее учесть
свойство
и далее учесть
свойство ![]() , а также (4.8), (4.9), (4.13) и
(4.14), (4.16). Таким образом, получаем равенства
, а также (4.8), (4.9), (4.13) и
(4.14), (4.16). Таким образом, получаем равенства
![\begin{displaymath}
m({\bf q}_{[j-1]}^0(m_{(j-1)},\nu_{(j-1)};\cdot))=
\sum_{s=1...
...[t_2^{[h_2(\tau_j)]},\vartheta]
l^{(s)}+m_{(j)}^{(s)}]=\mbox{}
\end{displaymath}](img467.gif)
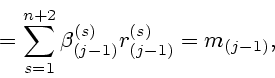
![\begin{displaymath}
M\{q^0_{[j-1],0}(m_{(j-1)},\nu_{(j-1)};\omega)\}=
\sum_{s=1}^{n+2}\beta_{(j-1)}^{(s)}c_{(j-1)}^{(s)}=\nu_{(j-1)},
\end{displaymath}](img469.gif)
![\begin{displaymath}
\mbox{}=
\sum_{s=1}^{n+2}\beta_{(j-1)}^{(s)} \times
[\Delta\...
...{\bf q}_{[j]}^0(m_{(j)}^{(s)},\nu_{(j)}^{(s)};\cdot))]=\mbox{}
\end{displaymath}](img471.gif)
![\begin{displaymath}
\mbox{}=
\sum_{s=1}^{n+2}\beta_{(j-1)}^{(s)}[\Delta\psi_{j-1...
...)+
\varphi_j^{'}(t_*;r_{(j-1)}^{(s)},c_{(j-1)}^{(s)})]=\mbox{}
\end{displaymath}](img472.gif)
Проверим выполнение свойства ![]() .
Возьмем
.
Возьмем
![]()
![]() и какую-то допустимую
и какую-то допустимую
![]() . Далее обозначим
. Далее обозначим
![\begin{displaymath}
g_{j-1}(t_*;{\bf q}_{[j-1]}(\cdot))=
\int \limits_{[\xi_{j-1...
...(t_*;\hat {\bf q}(\xi_{j-1};\cdot)\right)\right]d\xi_{j-1}\leq
\end{displaymath}](img499.gif)
![\begin{displaymath}
\leq\int \limits_{[\xi_{j-1}]}
\left[\Delta\psi_{j-1}(t_*;r(...
...{j-1}^{'}(t_*;r(\xi_{j-1}),c(\xi_{j-1}))\right]d\xi_{j-1} \leq
\end{displaymath}](img500.gif)
В силу индукции свойства ![]() ,
, ![]() справедливы
при
справедливы
при ![]() .
Принимая во внимание
.
Принимая во внимание ![]() ,
, ![]() ,
получаем, что верхняя грань в
(4.15) достигается на конечнозначной случайной величине
,
получаем, что верхняя грань в
(4.15) достигается на конечнозначной случайной величине
![]() ,
,
![]() , и (4.15) доказано.
Из (4.6) и (4.15) вытекает равенство
, и (4.15) доказано.
Из (4.6) и (4.15) вытекает равенство
![\begin{displaymath}
e(x[t_0[\cdot]t_*],\Delta_k)=\sum_{i_1=1}^{h_1(t_*)}\mu_1^{[i_1]}(x[t_1^{[i_1]}])+
\mbox{}
\end{displaymath}](img336.gif)
![\begin{displaymath}
\mbox{}+ \sup_{(m_{(1)},\nu_{(1)}) \in G_1(t_*)}
[(1-\nu_{(1...
...{[i_2]}])+
\langle m_{(1)},X[\vartheta,t_*]x_* \rangle+\mbox{}
\end{displaymath}](img505.gif)
Таким образом, вычисление стохастического программного экстремума ![]() сводится к построению рекуррентной последовательности выпуклых
сверху оболочек (4.7)-(4.14)
из детерминированной программной конструкции [6], [10],
предложенной для вычисления цены игры.
Согласно [10] величина (4.28) обладает свойством
сводится к построению рекуррентной последовательности выпуклых
сверху оболочек (4.7)-(4.14)
из детерминированной программной конструкции [6], [10],
предложенной для вычисления цены игры.
Согласно [10] величина (4.28) обладает свойством ![]() -стабильности.
-стабильности.
Рассмотрим теперь предельный переход в обсуждаемых конструкциях
при измельчении шага ![]() .
Используя лемму 3.1, свойство
.
Используя лемму 3.1, свойство ![]() -стабильности
величины (4.28), равенство (2.15),
следуя [6, стр. 147-151],
приходим к следующему утверждению.
-стабильности
величины (4.28), равенство (2.15),
следуя [6, стр. 147-151],
приходим к следующему утверждению.
![\begin{displaymath}
\lim_{k \to \infty}\rho(x[t_0[\cdot]t_*],\Delta_k)=
\lim_{k ...
...\infty}e(x[t_0[\cdot]t_*],\Delta_k)=
\rho^0(x[t_0[\cdot]t_*]),
\end{displaymath}](img515.gif)