

Next: 2 Стохастическая программная конструкция.
Up: KOVR1
Previous: KOVR1
Пусть система описывается уравнением
![\begin{displaymath}
{dx \over dt}=A(t)x+B(t)u+C(t)v,\ \ \ \
t\in [t_0,\vartheta],
\end{displaymath}](img1.gif) |
(1.1) |
где 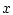 - фазовый вектор,
- фазовый вектор, 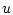 и
и 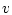 - векторы управлений первого и
второго игроков соответственно,
- векторы управлений первого и
второго игроков соответственно, 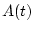 ,
, 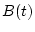 ,
, 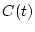 - непрерывные
при
- непрерывные
при
![$\ t\in [t_0,\vartheta]$](img9.gif) матрицы-функции;
матрицы-функции;
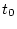 и
и 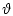 - фиксированные моменты времени (
- фиксированные моменты времени (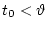 );
);
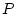 ,
, 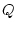 - выпуклые
компакты. Пусть имеются два разбиения отрезка времени
- выпуклые
компакты. Пусть имеются два разбиения отрезка времени
![$[t_0,\vartheta]$](img15.gif) :
:
![\begin{displaymath}
\Delta_{t_{\alpha}^{[i_{\alpha}]}}=\{t_{\alpha}^{[i_{\alpha}...
...pha}]},
\ i_{\alpha}=1,\ldots,N_{\alpha}-1\}, \quad \alpha=1,2
\end{displaymath}](img16.gif) |
(1.2) |
Заданы нормы
![$\mu_{\alpha}^{[i_{\alpha}]}(x)$](img18.gif) ,
, 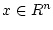 ,
,
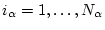 ,
, 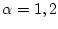 .
Допустимы измеримые по Борелю реализации
.
Допустимы измеримые по Борелю реализации
![$u[t_0[\cdot]\vartheta)=\{u[t]\in P,~ t_0\leq t< \vartheta\}$](img22.gif) и
и
![$v[t_0[\cdot]\vartheta)=
\{v[t]\in Q,~ t_0\leq t< \vartheta\}$](img23.gif) .
Такие реализации порождают единственным образом абсолютно непрерывные
движения
.
Такие реализации порождают единственным образом абсолютно непрерывные
движения
![$x[t_0[\cdot]\vartheta]=\{x[t],~ t_0\leq t\leq \vartheta,~x[t_0]=x_0\}$](img24.gif) системы (1.1) (
системы (1.1) (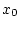 задано).
задано).
Показатель качества движений дан в виде функционала
![\begin{displaymath}
\gamma=\gamma(x[t_0[\cdot]\vartheta])=\sum_{i_1=1}^{N_1}\mu_...
...])
+\max_{1\leq i_2\leq N_2}\{\mu_2^{[i_2]}(x[t_2^{[i_2]}])\}.
\end{displaymath}](img26.gif) |
(1.3) |
При этом либо функционал 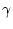 (1.3) задан априори, либо
он аппроксимирует исходный показатель, который оценивает
континуум значений
(1.3) задан априори, либо
он аппроксимирует исходный показатель, который оценивает
континуум значений ![$x[t]$](img28.gif) , реализовавшихся в процессе движения системы.
Задача построения управлений
, реализовавшихся в процессе движения системы.
Задача построения управлений 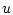 и
и 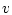 , которые нацелены на
минимизацию и максимизацию показателя качества (1.3) соответственно,
формализуется как антагонистическая дифференциальная игра [6].
Для всякой исходной истории
, которые нацелены на
минимизацию и максимизацию показателя качества (1.3) соответственно,
формализуется как антагонистическая дифференциальная игра [6].
Для всякой исходной истории
![$x[t_0[\cdot]t_*]$](img29.gif) ,
,
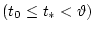 эта игра имеет цену
эта игра имеет цену
![$\rho^0(x[t_0[\cdot]t_*])$](img31.gif) и седловую точку
и седловую точку
![$\{u^0(x[t_0[\cdot]t],\varepsilon)$](img32.gif) ,
,
![$v^0(x[t_0[\cdot]t],\varepsilon)\}$](img33.gif) .
Здесь
.
Здесь
![$x[t_0[\cdot]t]=\{x[\tau],~ t_0\leq \tau\leq t\}$](img34.gif) - история
движения, реализовавшаяся к текущему моменту времени
- история
движения, реализовавшаяся к текущему моменту времени 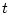
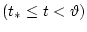 ;
;
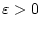 - некоторый параметр точности [2],[6].
Оптимальные стратегии
- некоторый параметр точности [2],[6].
Оптимальные стратегии
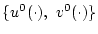 , строятся как экстремальные ([6], стр. 150) к
функционалу
, строятся как экстремальные ([6], стр. 150) к
функционалу 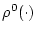 . Для такого построения оптимальных стратегий
достаточно уметь эффективно вычислять цену игры.
Настоящая статья посвящена вопросам вычисления цены игры
для каждой возможной текущей истории
. Для такого построения оптимальных стратегий
достаточно уметь эффективно вычислять цену игры.
Настоящая статья посвящена вопросам вычисления цены игры
для каждой возможной текущей истории
![$x[t_0[\cdot]t]$](img40.gif) как исходной.
как исходной.
2003-04-28
![\begin{displaymath}
{dx \over dt}=A(t)x+B(t)u+C(t)v,\ \ \ \
t\in [t_0,\vartheta],
\end{displaymath}](img1.gif)