

Next: 3 Стабильность стохастического программного
Up: KOVR1
Previous: 1 Постановка задачи.
Рассмотрим 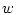 -модель, описываемую
дифференциальным уравнением
-модель, описываемую
дифференциальным уравнением
![\begin{displaymath}
{dw \over d\tau}=A(\tau)w+B(\tau)u+C(\tau)v,\ \ \ \ \tau\in[t_0,\vartheta] ,
\end{displaymath}](img42.gif) |
(2.1) |
где
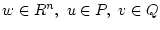 .
.
Пусть реализовалась история
![$w[t_0[\cdot]\tau_*]$](img44.gif) движения модели (2.1),
движения модели (2.1),
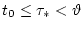 .
Назначим разбиение
.
Назначим разбиение
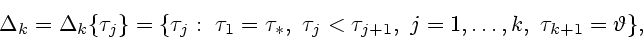 |
(2.2) |
в которое включим все моменты
![$t_{\alpha}^{[i_{\alpha}]}\geq \tau_*$](img47.gif) разбиений
разбиений
![$\Delta_{t_{\alpha}^{[i_{\alpha}]}}$](img48.gif) ,
, 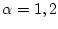 .
Рассмотрим вероятностное пространство
.
Рассмотрим вероятностное пространство 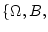 P
P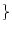 ,
элементарные события которого
,
элементарные события которого
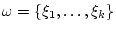 .
Здесь
.
Здесь
![$\xi_j \in [0,1],~j=1,\ldots,k$](img52.gif) - равномерно
распределенные случайные величины, связанные с моментами
- равномерно
распределенные случайные величины, связанные с моментами 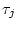 разбиения (2.2),
разбиения (2.2),
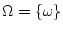 - единичный куб
в
- единичный куб
в  -мерном пространстве,
-мерном пространстве, 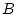 - борелевская
- борелевская 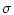 -алгебра
для этого куба, P=P(B) - лебегова мера, В
-алгебра
для этого куба, P=P(B) - лебегова мера, В 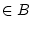 . Введем стохастические неупреждающие ([2, стр. 292]) программы
. Введем стохастические неупреждающие ([2, стр. 292]) программы
которые по совокупности аргументов являются измеримыми по Борелю
функциями. Символами
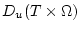 и
и
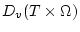 (здесь
(здесь
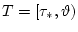 ) обозначим множества
всех допустимых программ (2.3) и (2.4) соответственно.
Из исходной позиции
) обозначим множества
всех допустимых программ (2.3) и (2.4) соответственно.
Из исходной позиции
![$\{\tau_*,w_*=w[\tau_*]\}$](img68.gif) программы
программы
![$u[\cdot]\in D_u(T\times\Omega)$](img69.gif) и
и
![$v[\cdot]\in D_v(T\times\Omega)$](img70.gif) порождают случайные
движения
порождают случайные
движения 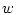 -модели ([2, стр. 292]), ([15, стр. 158])
-модели ([2, стр. 292]), ([15, стр. 158])
![\begin{displaymath}
w_{v[\cdot],u[\cdot]}[\tau,\omega]=X[\tau,\tau_*]w[\tau_*] +...
...\tau,\eta](B(\eta)u[\eta,\omega]+
C(\eta)v[\eta,\omega])d\eta,
\end{displaymath}](img71.gif) |
(2.5) |
где
![$~\tau \in [\tau_*,\vartheta],~ \omega\in \Omega$](img72.gif) ,
, ![$X[\tau,\eta]$](img73.gif) - фундаментальная матрица решений уравнения
- фундаментальная матрица решений уравнения
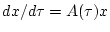 . Функции
. Функции
![$w_{v[\cdot],u[\cdot]}[\tau,\omega]$](img75.gif) будут измеримы по совокупности переменных
будут измеримы по совокупности переменных 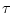 ,
, 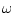 . На базе
. На базе
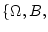 P
P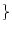 определим
линейное пространство
определим
линейное пространство
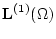 с элементами
с элементами
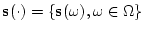 ,
,
![${\bf s}(\omega)=\{s_1^{[1]}(\omega),\ldots,s_1^{[N_1]}(\omega),$](img80.gif)
![$s_2^{[1]}(\omega),\ldots,s_2^{[N_2]}(\omega)\}$](img81.gif) ,
где компоненты
,
где компоненты
![$s_{\alpha}^{[i_{\alpha}]}(\omega)$](img82.gif) (
(
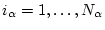
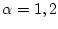 ) -
) - 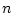 -мерные случайные
величины, определенные на
-мерные случайные
величины, определенные на 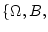 P
P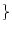 , для которых
, для которых
![$M\{\mu_{\alpha}^{[i_{\alpha}]}(s_{\alpha}^{[i_{\alpha}]}(\omega))\}< \infty$](img84.gif) . Здесь и далее символ
. Здесь и далее символ
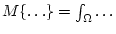 P
P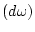 означает
математическое ожидание (интеграл Лебега) ([15, стр. 197]).
Определим также норму в
означает
математическое ожидание (интеграл Лебега) ([15, стр. 197]).
Определим также норму в
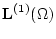 равенством
равенством
Пусть
![\begin{displaymath}
g_{\alpha}(\tau)=\min\{i_{\alpha}~:t_{\alpha}^{[i_{\alpha}]}\geq \tau\},
\quad \tau \in [t_0,\vartheta], \quad \alpha=1,2.
\end{displaymath}](img88.gif) |
(2.6) |
Реализовавшаяся история
![$w[t_0[\cdot]\tau_*]$](img44.gif) и пара стохастических
программ (2.3), (2.4) порождают в силу (2.5)
элемент
и пара стохастических
программ (2.3), (2.4) порождают в силу (2.5)
элемент
![${\bf y}(\cdot)={\bf y}(\cdot;w[t_0[\cdot]\tau_*],v[\cdot],u[\cdot],\Delta_k)$](img89.gif) из
из
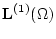 с компонентами
с компонентами
![$y_{\alpha}^{[i_{\alpha}]}(\omega)=w[t_{\alpha}^{[i_{\alpha}]}]$](img90.gif) ,
,
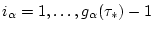 ,
,
![$y_{\alpha}^{[i_{\alpha}]}(\omega)=w_{v[\cdot],u[\cdot]}[t_{\alpha}^{[i_{\alpha}]},\omega]$](img92.gif) ,
,
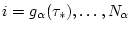 ,
, 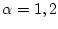 .
.
Следуя методу стохастического программного синтеза ([2],[6])
и принимая во внимание вид рассматриваемого функционала качества 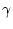 (1.3), введем величину стохастического программного максимина
(1.3), введем величину стохастического программного максимина
![\begin{displaymath}
\rho(w[t_0[\cdot]\tau_*],\Delta_k\{\tau_j\})=
\sup_{v[\cdot]...
...mega)}\Vert{\bf y}(\cdot)\Vert,
\quad t_0\leq\tau_*<\vartheta,
\end{displaymath}](img94.gif) |
(2.7) |
Удобно перейти к двойственному описанию величины (2.7).
Через
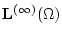 обозначим пространство
случайных величин
обозначим пространство
случайных величин
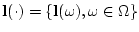 ,
,
![${\bf l}(\omega)=\{l_1^{[1]}(\omega),\ldots,l_1^{[N_1]}(\omega)$](img97.gif) ,
,
![$l_2^{[1]}(\omega)$](img98.gif) ,
,
![$\ldots,l_2^{[N_2]}(\omega)\}$](img99.gif) ,
где компоненты
,
где компоненты
![$l_{\alpha}^{[i_{\alpha}]}(\omega)$](img100.gif) -
- 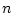 -мерные случайные
величины, определенные на
-мерные случайные
величины, определенные на 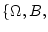 P
P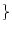 , для которых
, для которых
![$\displaystyle \mathrm{vrai}\max_{\omega \in \Omega}\mu_{\alpha}^{*[i_{\alpha}]}
(l_{\alpha}^{[i_{\alpha}]}(\omega)) < \infty$](img101.gif) .
Здесь
.
Здесь
![$\mu_{\alpha}^{*[i_{\alpha}]}(\cdot)$](img102.gif) - норма, сопряженная с нормой
- норма, сопряженная с нормой
![$\mu_{\alpha}^{[i_{\alpha}]}(\cdot)$](img103.gif) ,
,
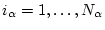 ,
, 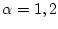 .
Норму в
.
Норму в
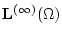 введем по формуле
введем по формуле
Пусть
![\begin{displaymath}
h_{\alpha}(\tau)=\max\{i_{\alpha}~:t_{\alpha}^{[i_{\alpha}]}\le \tau\},
\quad \tau \in [t_0,\vartheta], \quad \alpha=1,2.
\end{displaymath}](img106.gif) |
(2.8) |
(Если нет ни одного номера  такого, что
такого, что
![$t_{\alpha}^{[i_{\alpha}]}\le \tau$](img108.gif) ,
полагаем
,
полагаем
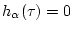 ). Обозначим
). Обозначим
![\begin{displaymath}
\mbox{}+
\sum_{i_2=g_2(\tau_{*})}^{N_2}{X^T[t_2^{[i_2]},\vartheta]
M\{l_2^{[i_2]}(\omega)\}},
\end{displaymath}](img111.gif) |
(2.9) |
![\begin{displaymath}
+\sum_{i_2=h_2(\tau_{j})+1}^{N_2}
{X^T[t_2^{[i_2]},\vartheta]M\{l_2^{[i_2]}(\omega)\vert\xi_1,\ldots,\xi_j\}},
~j=1,\ldots,k.
\end{displaymath}](img113.gif) |
(2.10) |
Здесь
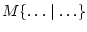 - условное математическое ожидание.
- условное математическое ожидание.
Определим величину программного экстремума
![\begin{displaymath}
\begin{array}{c} \displaystyle
e(w[t_0[\cdot]\tau_*],\Delta_...
...{\bf l}(\cdot)),\\ [2ex]
t_0\leq\tau_*<\vartheta.
\end{array}\end{displaymath}](img115.gif) |
(2.11) |
Здесь
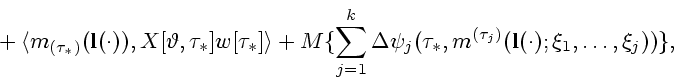 |
(2.12) |
![\begin{displaymath}
\mbox{}+
\sum_{i_2=1}^{g_2(\tau_*)-1}\langle M\{l_2^{[i_2]}(\omega)\},w[t_2^{[i_2]}]\rangle,
\end{displaymath}](img119.gif) |
(2.13) |
![\begin{displaymath}
\begin{array}{c}
\displaystyle
\Delta\psi_j(\tau_*;m)=
\int ...
...e d\tau,\\ [3ex]
\quad m\in R^n,\quad j=1,\ldots,k,
\end{array}\end{displaymath}](img120.gif) |
(2.14) |
где
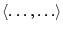 - скалярное произведение векторов.
При этом в (2.13) результат суммирования по убывающему индексу
полагаем равным нулю. Отметим, что
- скалярное произведение векторов.
При этом в (2.13) результат суммирования по убывающему индексу
полагаем равным нулю. Отметим, что
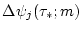 - непрерывные
по
- непрерывные
по 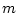 функции.
функции.
Проверим, что для всякой исходной истории
![$w[t_0[\cdot]\tau_*]$](img44.gif) ,
,
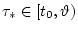 при всяком разбиении
при всяком разбиении 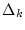 (2.2) справедливо равенство
(2.2) справедливо равенство
![\begin{displaymath}
\rho(w[t_0[\cdot]\tau_*],\Delta_k)=e(w[t_0[\cdot]\tau_*],\Delta_k).
\end{displaymath}](img126.gif) |
(2.15) |
Пусть зафиксирована стохастическая программа
![$v^*[\cdot]\in D_v(T\times\Omega)$](img127.gif) . Перебирая все программы
. Перебирая все программы
![$u[\cdot]\in D_u(T\times\Omega)$](img69.gif) получим множество:
получим множество:
случайных величин
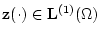 .
Это множество будет непустым и выпуклым.
Обозначим
.
Это множество будет непустым и выпуклым.
Обозначим
![\begin{displaymath}
\left({\bf l}(\cdot),{\bf s}(\cdot)\right)
=\int \limits_\Om...
...}(\omega),
s_2^{[i_2]}(\omega)\right>\right ]{\rm P}(d\omega).
\end{displaymath}](img130.gif) |
(2.16) |
Согласно [12, стр. 153] любой линейный функционал,
определенный на элементах
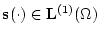 представим в виде (2.16) при
представим в виде (2.16) при
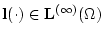 . Опираясь на теорему об отделимости выпуклых множеств
(см. [11, стр. 107])
можно показать, что для всякой программы
. Опираясь на теорему об отделимости выпуклых множеств
(см. [11, стр. 107])
можно показать, что для всякой программы
![$v[\cdot]\in D_v(T\times\Omega)$](img70.gif) имеет место равенство
имеет место равенство
![\begin{displaymath}
\inf_{{\bf z}(\cdot) \in Z(v[\cdot])}\sup_{\Vert {\bf l}(\cd...
... \in Z(v[\cdot])}
\left({\bf l}(\cdot),{\bf z}(\cdot)\right).
\end{displaymath}](img133.gif) |
(2.17) |
Далее принимая во внимание (2.5), (2.13),(2.16),
неупреждаемость программ (2.3), (2.4)
и определение условного математического ожидания, вычисляем
![\begin{displaymath}
\left. \vphantom{\sum_{j=1}^k}
\mbox{}+ C(\tau)v[\tau,\xi_1,\ldots,\xi_j])\rangle d\tau \right\}.
\end{displaymath}](img136.gif) |
(2.18) |
Построим стохастические программы ![$u^0[\cdot]$](img137.gif) ,
, ![$v^0[\cdot]$](img138.gif) из условий
из условий
Так построенные программы допустимы, так что
![$u^0[\cdot]\in D_u(T\times\Omega)$](img145.gif) ,
,
![$v^0[\cdot]\in D_v(T\times\Omega)$](img146.gif) .
Поэтому из (2.12)-(2.14), (2.18)-(2.20) вытекает равенство
.
Поэтому из (2.12)-(2.14), (2.18)-(2.20) вытекает равенство
![\begin{displaymath}
\sup_{v[\cdot]}
\inf_{{\bf z}(\cdot) \in Z(v[\cdot])}\left({...
...t)\right)=
\chi (w[t_0[\cdot]\tau_*],\Delta_k,{\bf l}(\cdot)).
\end{displaymath}](img147.gif) |
(2.21) |
Из (2.17), используя затем возможность
перестановки местами двух операций взятия верхней грани и
учитывая (2.21), получаем равенства
которые, согласно (2.11), доказывают равенство (2.15).
Обратимся теперь к случаю, когда
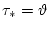 .
В этом случае величины
.
В этом случае величины 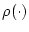 и
и 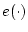 определим формально
равенствами
определим формально
равенствами
![$\rho(w[t_0[\cdot]\vartheta],\Delta_k)=$](img153.gif)
![$e(w[t_0[\cdot]\vartheta],\Delta_k)=$](img154.gif)
![$\gamma(w[t_0[\cdot]\vartheta]),$](img155.gif) где теперь символом
где теперь символом 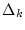 обозначено множество,
состоящее из одной точки
обозначено множество,
состоящее из одной точки
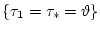 .
.


Next: 3 Стабильность стохастического программного
Up: KOVR1
Previous: 1 Постановка задачи.
2003-04-28
![]() -модель, описываемую
дифференциальным уравнением
-модель, описываемую
дифференциальным уравнением
![]() движения модели (2.1),
движения модели (2.1),
![]() .
Назначим разбиение
.
Назначим разбиение
![\begin{displaymath}
\Vert{\bf s}(\cdot)\Vert=M\left\{\sum\limits_{i_1=1}^{N_1}\m...
...eq i_2\leq N_2}\{\mu_2^{[i_2]}(s_2^{[i_2]}(\omega))\}\right\}.
\end{displaymath}](img87.gif)
![]() и пара стохастических
программ (2.3), (2.4) порождают в силу (2.5)
элемент
и пара стохастических
программ (2.3), (2.4) порождают в силу (2.5)
элемент
![]() из
из
![]() с компонентами
с компонентами
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
![]() (1.3), введем величину стохастического программного максимина
(1.3), введем величину стохастического программного максимина
![\begin{displaymath}
\Vert{\bf l}(\cdot)\Vert^*=
\max \left\{\max_{1 \leq i_1\leq...
...\max_{\omega \in \Omega}\mu_1^{*[i_1]}(l_1^{[i_1]}(\omega))\},
\end{displaymath}](img104.gif)
![\begin{displaymath}
\left.
\mathrm{vrai}\max_{\omega \in \Omega}\sum_{i_2=1}^{N_2} \mu_2^{*[i_2]}(l_2^{[i_2]}(\omega))\right\}.
\end{displaymath}](img105.gif)
![\begin{displaymath}
m_{(\tau_*)}({\bf l}(\cdot))=\sum_{i_1=g_1(\tau_{*})}^{N_1}{X^T[t_1^{[i_1]},\vartheta]
M\{l_1^{[i_1]}(\omega)\}}+ \mbox{}
\end{displaymath}](img110.gif)
![\begin{displaymath}
m^{(\tau_j)}({\bf l}(\cdot);\xi_1,\ldots,\xi_j)=\sum_{i_1=h_...
...heta]M\{l_1^{[i_1]}(\omega)\vert\xi_1,\ldots,\xi_j\}}+ \mbox{}
\end{displaymath}](img112.gif)
![\begin{displaymath}
\sigma (w[t_0[\cdot]\tau_*],{\bf l}(\cdot))=\sum_{i_1=1}^{g_...
...\langle M\{l_1^{[i_1]}(\omega)\},w[t_1^{[i_1]}]\rangle+\mbox{}
\end{displaymath}](img118.gif)
![]() ,
,
![]() при всяком разбиении
при всяком разбиении ![]() (2.2) справедливо равенство
(2.2) справедливо равенство
![]() . Перебирая все программы
. Перебирая все программы
![]() получим множество:
получим множество:
u[\tau,\xi_1,\ldots,\xi_j]+\mbox{}
\right.
\end{displaymath}](img135.gif)
![]() ,
, ![]() из условий
из условий
![]() ,
,
![]() .
Поэтому из (2.12)-(2.14), (2.18)-(2.20) вытекает равенство
.
Поэтому из (2.12)-(2.14), (2.18)-(2.20) вытекает равенство
![\begin{displaymath}
\rho(w[t_0[\cdot]\tau_*],\Delta_k)=\sup_{v[\cdot]}\inf_{{\bf...
...t) \Vert^* \leq 1}
\left({\bf l}(\cdot),{\bf z}(\cdot)\right)=
\end{displaymath}](img148.gif)
![\begin{displaymath}
=\sup_{\Vert {\bf l}(\cdot) \Vert^* \leq 1}
\sup_{v[\cdot]}\...
...^* \leq 1}
\chi (w[t_0[\cdot]\tau_*],\Delta_k,{\bf l}(\cdot)),
\end{displaymath}](img149.gif)
![]() .
В этом случае величины
.
В этом случае величины ![]() и
и ![]() определим формально
равенствами
определим формально
равенствами
![]()
![]()
![]() где теперь символом
где теперь символом ![]() обозначено множество,
состоящее из одной точки
обозначено множество,
состоящее из одной точки
![]() .
.