6. Слабая и сильная инвариантность в конструкции левостроронних решений

Приведем условия, которые характеризуют ЛР задачи (2.1)-(3.1) в терминах производных по направлениям. Сначала приведем утверждение, которое характеризует ЛР с помощью сильной и слабой инвариантности множеств.

Утверждение 5   Полунепрерывная снизу функция $c_{0}(\cdot):G^{*} \rightarrow R^1$ является ЛР задачи $(\ref{2.1})$, $(\ref{3.1})$ тогда и только тогда, когда $c(0, x)=\sigma(x)$ при всех $x\in R^n ,$ а множество $\mathrm{epi}\ c(\cdot)$ является положительно слабо и отрицательно сильно инвариантным относительно ДВ $(\ref{2.4})$.

Справедливость утверждения следует из определения 3.1 и теоремы 1.1 работы [21].

Сформулируем утверждение, характеризующее ЛР в инфинитезимальной форме. Для функции $c(\cdot):G \rightarrow R^1$ обозначим

$$\frac{\partial^{-}c(t, x)}{\partial (\alpha , d)} = \display... ...+\delta \cdot \beta , x+\delta \cdot y)- c(t, x)] \delta^{-1},$$

$$\alpha (t, x, s)=\sup \ <s, d> \quad \hbox{при} \quad d\in \{ d: \frac{\partial^{-}c(t, x)}{\partial (1, d)}\leq 0 \},$$

$$\beta (t, x, s)=\inf \,<s, d> \quad \hbox{при} \quad d\in \{ d: \frac{\partial^{-}c(t, x)}{\partial (-1, -d)}\leq 0 \}.$$

Утверждение 6   Полунепрерывная снизу функция $c(\cdot):G^{*} \rightarrow R^1$ является ЛР задачи $(\ref{2.1})$, $(\ref{3.1})$ тогда и только тогда, когда $c(0, x)=\sigma(x)$ при всех $x\in R^n$ и выполняются неравенства

$$\displaystyle {\min_{f\in F(t, x)}} \ \frac{\partial^{-}c(t,... ...(t, x)}} \ \frac{\partial^{-}c(t, x)}{\partial (-1, -f)}\leq 0$$ (6.1)

при всех $(t, x)\in G,$ или же неравенства

$$\beta (t, x, s) \leq \xi (t, x, s) \leq \alpha (t, x, s)$$ (6.2)

при всех $(t, x, s)\in G \times R^n.$

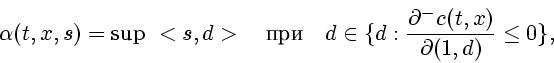
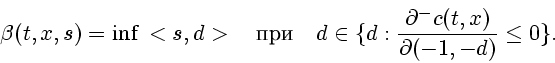
Д о к а з а т е л ь с т в о. Пусть $(t_{0}, x_{0})\in G^{*}$ - произвольная фиксированная точка. Обозначим

$$W_{c(t_{0}, x_{0})}^{-}=\{ (t, x)\in G^{*} : c(t, x)\leq c(t_{0}, x_{0})\} .$$

Из утверждения 5 следует, что для того чтобы функция $c(\cdot):G^{*} \rightarrow R^1$ была ЛР задачи (2.1)-(3.1), необходимо и достаточно, чтобы выполнялось $c(0, x)=\sigma(x)$ при всех $x\in R^n ,$ а множество $W_{c(t_{0}, x_{0})}^{-}$ было положительно слабо инвариантным и отрицательно сильно инвариантным относительно ДВ (2.3) при всех $(t_{0}, x_{0}) \in G^{*}.$ Далее, из теорем 2.2 и 2.3 работы [21], которые характеризуют слабую и сильную инвариантность множеств $W_{c(t_{0}, x_{0})}^{-}$ ( $(t_{0}, x_{0})\in G^{*}$), вытекает справедливость утверждения.

Отметим, что если ЛР $c(\cdot):G^{*} \rightarrow R^1$ задачи (2.1)-(3.1) в точке $(t, x)$ дифференцируемо, то из неравенств (6.1) или (6.2) следует, что функция $c(\cdot)$ в точке $(t, x)$ удовлетворяет уравнению (2.1).

Пусть функция $\omega (\cdot): G^{*} \rightarrow R^1$ является минимаксным решением уравнения (2.1), удовлетворяющим краевому условию

$$\omega (\theta, x)=\sigma_{1}(x) \quad \hbox{при всех} \quad x\in R^n,$$ (6.3)

где функция $\sigma_{1}(\cdot):R^n \rightarrow R^1$ непрерывна. Известно (см., например, [8, 9]), что при выполнении условий 2a)-2e), минимаксное решение задачи (2.1)-(3.1) существует и единственно, а функция $\omega (\cdot): G^{*} \rightarrow R^1$ непрерывна. Обозначим $\sigma_{2}(x)=\omega(0, x).$ Тогда функция $\sigma_{2}(\cdot):R^n \rightarrow R^1$ непрерывна. Множество ЛР уравнения (2.1), удовлетворяющих начальному условию $c(0, x)=\sigma_{2}(x)$ при всех $x\in R^n ,$ обозначим символом ${\mathrm{Sol}}_{*}.$ Справедливо

Утверждение 7   $\omega(\cdot)\in {\mathrm{Sol}}_{*}.$

Д о к а з а т е л ь с т в о. Так как функция $\omega (\cdot): G^{*} \rightarrow R^1$ является минимаксным решением задачи (2.1)-(3.1), то согласно [8, 9] эта функция непрерывна, множество $\mathrm{epi}\ \omega (\cdot)$ является положительно слабо инвариантным, а множество $\mathrm{hypo}\,\omega(\cdot)$ положительно сильно инвариантным относительно ДВ (2.4). Тогда из теоремы 1.1 работы [24] вытекает, что $\mathrm{epi}\ \omega(\cdot)=\tilde{H}_{-}(\theta , \mathrm{epi}\ \omega(\theta, \cdot)),$ где $\omega(0, x)=\sigma_{2}(x),$ и, следовательно, $\omega(\cdot)\in \mathrm{Sol}_{*}.$