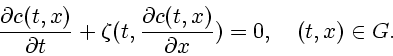 |
(7.1) |
В заключение рассмотрим ЛР дифференциального уравнения с частными
производными первого порядка вида
Предполагается, что функция
![]() удовлетворяет условиям 2a), 2c)-2e). Тогда нетрудно установить, что
множество
удовлетворяет условиям 2a), 2c)-2e). Тогда нетрудно установить, что
множество ![]() определенное соотношением (2.2), будет иметь вид
определенное соотношением (2.2), будет иметь вид
![\begin{displaymath}
P(t)=\{ f\in R^n : \displaystyle {\min_{s\in R^n}} \ [<s, f>-\zeta(t, s)]\geq 0\},
\end{displaymath}](img292.gif)
Совокупность решений ДВ (7.2) (на отрезке ![]() удовлетворяющих условию
удовлетворяющих условию
![]() где
где
![]() обозначим символом
обозначим символом
![]() Положим
Положим
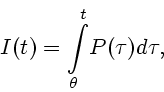
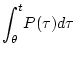 есть интеграл от многозначного
отображения
есть интеграл от многозначного
отображения
Для множеств ![]()
![]() полагаем
полагаем
Совокупность ЛР задачи (7.1), удовлетворяющих начальному условию
(3.1), обозначим символом
![]() и положим
и положим
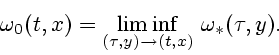
Справедливо
Поступила 23.07.2000