3. Основная задача и примеры

Рассмотрим решение уравнения (2.1), удовлетворяющее начальному условию

$$c(0, x) = \sigma(x) \ \ \hbox{при всех} \ \ x\in R^n ,$$ (3.1)

где $\sigma(\cdot) : R^n \rightarrow R^1$ - непрерывная функция.

Пусть $c(\cdot):[0, \theta ] \times R^n \rightarrow R^1$ - некоторая функция. Напомним, что надграфик и подграфик функции $c(\cdot)$ определяются соотношениями

$$\mathrm{epi}\ c(\cdot) =\{ (t, x, \alpha) \in G^{*} \times R^1 :c(t, x) \leq \alpha \} ,$$

$$\mathrm{hypo}\ c(\cdot) =\{ (t, x, \alpha) \in G^{*} \times R^1 :c(t, x) \geq \alpha \} .$$

Сформулируем определение ЛР задачи (2.1)-(3.1).

О п р е д е л е н и е 3.1. Полунепрерывная снизу функция $c(\cdot):G^{*} \rightarrow R^1,$ называется ЛР задачи (2.1)-(3.1) на множестве $G^{*},$ если она удовлетворяет начальному условию (3.1) и

$$\mathrm{epi}\ c(\cdot)=\tilde{H}_{-}(\theta, \mathrm{epi}\ c(\theta, \cdot)).$$ (3.2)

Здесь $\mathrm{epi}\ c(\theta, \cdot) =\{ (x, \alpha) \in \times R^n \times R^1 : c(\theta, x) \leq \alpha \} .$

Негладкие решения уравнения (2.1), удовлетворяющие краевому условию

$$c(\theta, x) = \sigma(x) \quad \hbox{при всех} \quad x\in R^n,$$ (3.3)

исследовались в теории минимаксных решений уравнения Гамильтона-Якоби (см., например, [4-6, 8-10, 13, 14]). Приведем определение минимаксного решения в случае, когда гамильтониан уравнения (2.1) $\xi(\cdot) : G^{*} \times R^n \rightarrow R^1$ удовлетворяет условиям 2a)-2c).

О п р е д е л е н и е 3.2. [8, стр. 15; 9]. Непрерывная функция $c(\cdot):G^{*} \rightarrow R^1$ называется минимаксным решением задачи (2.1)-(3.3) на множестве $G^{*},$ если $c(\theta , x) = \sigma(x)$ при всех $x\in R^n ,$ множество $\mathrm{epi}\ c(\cdot)$ положительно слабо инвариантно, множество $\mathrm{hypo}\,c(\cdot)$ положительно сильно инвариантно относительно ДВ (2.4).

Воспользовавшись теоремой 1.1 из pаботы [24], можно установить, что если функция $c(\cdot):G^{*} \rightarrow R^1$ является минимаксным решением задачи (2.1)-(3.3), то для этой функции выполняется соотношение (3.2). А если непрерывная функция $c(\cdot):G^{*} \rightarrow R^1$ является ЛР задачи (2.1)-(3.1), то множество $\mathrm{epi}\ c(\cdot)$ является положительно слабо инвариантным, а множество $\mathrm{hypo}\,c(\cdot)$ - положительно сильно инвариантным относительно ДВ (2.4). Обозначим

$$W_{\alpha}^{-}=\{ (t, x)\in G^{*} :c(t, x) \leq \alpha \} , \quad N_{\alpha}^{-}=\{ x\in R^n :c(\theta, x) \leq \alpha \} .$$

Справедливо утверждение, характеризующее ЛР с помощью множеств Лебега.

Утверждение 1   Для того, чтобы полунепрерывная снизу функция $c(\cdot):G^{*} \rightarrow R^1$ была ЛР задачи $(\ref{2.1})$-$(\ref{3.1})$, необходимо и достаточно, чтобы она удовлетворяла начальному условию $(\ref{3.1})$, и при всех $\alpha \in R^1$ выполнялось соотношение

$$W_{\alpha}^{-}= H_{-}(\theta, N_{\alpha}^{-}).$$ (3.4)

Известно (см., например, [8, 9]), что минимаксное решение задачи (2.1)-(3.3) при условиях 2a)-2e) всегда существует и единственно.

Геометрически это объясняется тем, что $Z(t;\theta, \mathrm{epi}\ \sigma(\cdot)) \neq \hbox{\O}$ при всех $t\in [0, \theta ]$ и множество $\tilde{H}_{-}(\theta, \mathrm{epi}\ \sigma(\cdot))$ определяется единственным образом. Однако существование и единственность ЛР выглядит немного иначе. Существование ЛР задачи (2.1)-(3.1) обусловлено наличием полунепрерывной снизу функции $c(\cdot):G^{*} \rightarrow R^1$ такой, что выполняются соотношения (3.2) и $\mathrm{epi}\ \sigma(\cdot)=Z(0;\theta, \mathrm{epi}\ c(\theta, \cdot)).$

Единственность ЛР задачи (2.1)-(3.1) зависит от того, единственна ли функция, удовлетворяющая этим соотношениям. Отметим, что несмотря на выполнение условий 2a)-2e), котоpые гаpантиpуют существование и единственность минимаксных pешений задачи (2.1)-(3.3) (см., напpимеp, [8, 9]), ЛР задачи (2.1)-(3.1) может оказаться не единственным или же может вообще не существовать. Эти обстоятельства проиллюстрируем на следующих примерах.

П р и м е р 3.1. Пусть уравнение (2.1) имеет вид

$$\frac{\partial c(t, x)}{\partial t} - \left\vert \frac{\partial c(t, x)}{\partial x} \right\vert = 0,$$ (3.5)

где $t\in [0, 1],$ $x\in R^1 ,$ а начальное условие задано как

$$c(0, x) =\sigma(x)= \left\{ \begin{array}{lll} & x-2 & \mbo... ...box{при} \hspace{0.4cm} x\in (-\infty, -2). \end{array}\right.$$ (3.6)

Можно проверить, что $F(t, x)= [-1, 1],$ а функции

$$c_{1}(t, x) = \left\{ \begin{array}{lll} & x+t-2 & \mbox{пр... ...-x+t-2 & \mbox{при} \hspace{0.4cm} x-t+2<0, \end{array}\right.$$ (3.7)

$$c_{2}(t, x) = \left\{ \begin{array}{lll} & x+t-2 & \mbox{при... ...-x+t-2 & \mbox{при} \hspace{0.4cm} x-t+2<0, \end{array}\right.$$

являются ЛР задачи (3.5)-(3.6). Однако $c_{1}(1, x) \neq c_{2}(1, x)$ при $x\in (-1, 1).$ Таким образом, ЛР задачи (3.5)-(3.6) не является единственным.

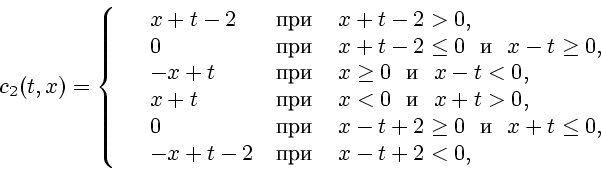
П р и м е р 3.2. Пусть уравнение (2.1) имеет вид

$$\frac{\partial c(t, x)}{\partial t} - \left\vert \frac{\partial c(t, x)}{\partial x} \right\vert = 0,$$ (3.8)

где $t\in [0, 1],$ $x=(x_{1}, x_{2})\in R^2 ,$ а начальное условие задано соотношением

$$c(0, x) =\sigma(x)= \parallel x\parallel =\sqrt{x_{1}^{2}+x_{2}^{2}}.$$ (3.9)

Нетрудно установить, что

$$F(t, x_{1}, x_{2})=\{ f=(f_{1}, f_{2})\in R^2 : \parallel f\parallel = \sqrt{f_{1}^{2}+f_{2}^{2}} \leq 1\}$$ (3.10)

при всех $(t, x_{1}, x_{2})\in [0, 1]\times R^2 .$

Рассмотрим ДВ

$$\dot{x}(t) \in F(t, x(t)),$$ (3.11)

где $x(t)=(x_{1}(t), x_{2}(t)),$ а множество $F(t, x_{1}(t), x_{2}(t))$ определено соотношением (3.10).

Если функция $c(\cdot):[0, 1]\times R^2 \rightarrow R^1$ является ЛР задачи (3.8)-(3.9), то, согласно утверждению 1, для любого $\alpha \in R^1$ должно выполняться соотношение $M_{\alpha}= X(0;1, N_{\alpha}),$ где $M_{\alpha}= \{ x\in R^2 :\sigma(x)=\parallel x \parallel \leq \alpha \} ,$ $N_{\alpha}=\{ x\in R^2 :c(1, x)\leq \alpha\} ,$ $X(0;1, N_{\alpha})= \{x(0)\in R^2 : x(\cdot) \in X(1, N_{\alpha}),$ $X(1, N_{\alpha})$ - совокупность решений ДВ (3.11), удовлетворяющих условию $x(1)\in N_{\alpha}.$ Однако легко проверить, что при $\alpha \in [0, 1)$ не существует множество $N_{\alpha} \subset R^2$ такое, чтобы выполнялось $X(0;1, N_{\alpha})=\{ x\in R^2 :\parallel x\parallel \leq \alpha \}.$ Таким образом, ЛР задачи (3.8)-(3.9) не существует.

Отметим, что ЛР задачи (2.1)-(3.1) может оказаться полунепрерывной снизу функцией.

П р и м е р 3.3. Рассмотрим функцию

$$c_{*}(t, x) = \left\{ \begin{array}{lll} & x+t-2 & \mbox{пр... ...-x+t-2 & \mbox{при} \hspace{0.2cm} x-t+2<0. \end{array}\right.$$ (3.12)

Можно проверить, что полунепpеpывная снизу функция $c_{*}(\cdot) :[0, 1] \times R^2 \rightarrow R^1,$ определенная соотношением (3.12), является ЛР задачи
(3.5)-(3.6).