

Next: Bibliography
Up: ANANIEV
Previous: 6 Обобщение процедуры фильтрации
Опишем в заключение некоторые классы систем
(1.1)-(1.3), удовлетворяющие предположению 5.1.
Прежде всего, рассмотрим многошаговые включения
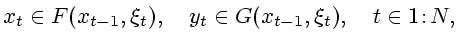 |
(7.1) |
где 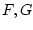 суть многозначные отображения с компактными
значениями. Система (7.1) сводится к (1.1)-(1.3),
если положить
суть многозначные отображения с компактными
значениями. Система (7.1) сводится к (1.1)-(1.3),
если положить
Определим многозначные отображения
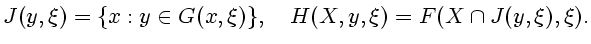 |
(7.2) |
Тогда случайные информационные множества для
системы (7.1) определятся рекуррентными соотношениями
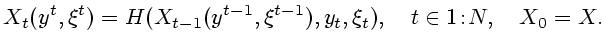 |
(7.3) |
Кроме того, для сигнала должны выполняться включения
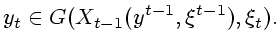 |
(7.4) |
В том
случае, когда отображения 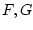 системы (7.1) непрерывны по
Хаусдорфу, а пространство
системы (7.1) непрерывны по
Хаусдорфу, а пространство 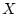 - компакт, в качестве пространства
- компакт, в качестве пространства
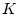 берем множество непустых компактных подмножеств с
хаусдорфовой метрикой. В этом случае предположение 5.1
выполняется. Случай, когда
берем множество непустых компактных подмножеств с
хаусдорфовой метрикой. В этом случае предположение 5.1
выполняется. Случай, когда
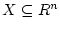 и не компактно,
рассмотрен в работе [7].
и не компактно,
рассмотрен в работе [7].
Пусть теперь 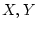 суть вещественные сепарабельные гильбертовы
пространства, а
суть вещественные сепарабельные гильбертовы
пространства, а 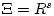 . Задана линейная система
. Задана линейная система
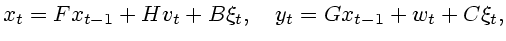 |
(7.5) |
где
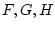 - ограниченные линейные операторы, а
- ограниченные линейные операторы, а 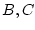 -
конечномерные линейные операторы, причем оператор
-
конечномерные линейные операторы, причем оператор 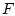 имеет
ограниченный обратный. Ограничения типа (1.3) заданы в виде
имеет
ограниченный обратный. Ограничения типа (1.3) заданы в виде
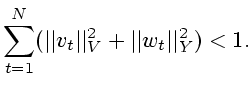 |
(7.6) |
Для этой
квадратичной задачи функции (3.1) подсчитываются
непосредственно. Они имеют вид:
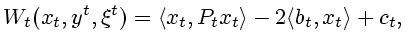 |
(7.7) |
где
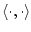 -
скалярное произведение в пространстве
-
скалярное произведение в пространстве 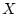 , а параметры
определяются рекуррентным образом:
, а параметры
определяются рекуррентным образом:
![\begin{displaymath}\begin{array}{c} P_t=F^{*-1}(P_{t-1}+G^*G-(P_{t-1}+G^*G)T_t(P...
...1}+\\ [2ex] +G^*G) F^{-1}B\xi_t\rangle,\quad c_0=0. \end{array}\end{displaymath}](img298.gif) |
(7.8) |
Следовательно, множества (3.4) допустимых
неопределенных факторов можно описать неравенством
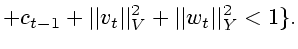 |
(7.9) |
В качестве параметра 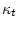 берем пару
берем пару
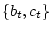 . Тогда предположение 5.1, очевидно,
выполнено.
. Тогда предположение 5.1, очевидно,
выполнено.
Мы описали два простых класса систем, удовлетворяющих
предположению 5.1. Достаточно жесткие предположения об
указанных классах могут быть сняты. В частности, может быть
снято требование об обратимости оператора 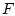 в уравнениях
(7.5) при условии полной наблюдаемости (см. [1])
системы (7.5).
в уравнениях
(7.5) при условии полной наблюдаемости (см. [1])
системы (7.5).
Поступила 13.03.00


Next: Bibliography
Up: ANANIEV
Previous: 6 Обобщение процедуры фильтрации
2003-06-05
![$\displaystyle h(x,v,w,\xi)=\left\{\begin{array}{cl}0,&v\in F(x,\xi)\mbox{ и } w\in G(x,\xi),\\ [2ex]+\infty,&\mbox{в противном случае}.\end{array}\right.$](img285.gif)
![]() суть вещественные сепарабельные гильбертовы
пространства, а
суть вещественные сепарабельные гильбертовы
пространства, а ![]() . Задана линейная система
. Задана линейная система ![]() в уравнениях
(7.5) при условии полной наблюдаемости (см. [1])
системы (7.5).
в уравнениях
(7.5) при условии полной наблюдаемости (см. [1])
системы (7.5).