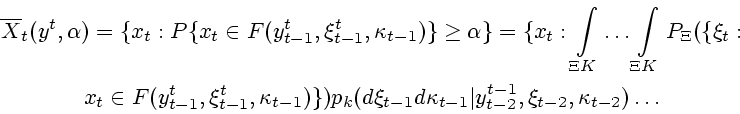5. Построение множеств информационной надежности при дополнительных предположениях

Далее названием "множества информационной надежности" объединяем совокупности, определенные согласно (3.10) либо (4.1). Из содержания предыдущих пунктов и примеров ясно, что построить рекуррентные определяющие соотношения для рассматриваемых множеств в общем случае не всегда возможно. Поэтому введем некоторые предположения, которые гарантируют рекурсивность по крайней мере для случайных информационных множеств. Они пригодятся также и в дальнейшем для обобщения процедуры фильтрации.

Предположение 5.1   Для системы (1.1)-(1.3) существуют борелевское пространство $K$ и функциональные соотношения такие, что

$$\begin{array}{rcl}\kappa _1\!\!\!&=&\!\!\!k_1(y_1,\xi_1),\\ [... ...{t-1},\xi^t_{t-1},\kappa _{t-1}),\quad t\in 2\!:\!N,\end{array}$$ (5.1)

где $k_1:Y\Xi\to K$ и $k:Y^2\Xi^2K\to K$ - универсально измеримые функции, а многозначное отображение $\overline{\cal H}$ измеримо в том смысле, что $\{(y,\xi^2,\kappa ):\overline{\cal H}(y,\xi^2,\kappa )\cap\mathcal{F}\neq\emptyset\}\in U_{Y\Xi^2K}$ для любого замкнутого множества ${\cal F}\subseteq XV$. Здесь и далее символом $U_X$ обозначается $\sigma$-алгебра универсально измеримых множеств пространства $X$. Кроме того, предполагается, что множество $\cal G$ всех универсально измеримых селекторов [13] многозначного отображения

$$G(y,\xi^2,\kappa )=g(\overline{\cal H}(y,\xi^2,\kappa ),\xi_2)$$ (5.2)

непусто.

Прежде чем обсудить данное предположение, напомним определение универсально измеримых множеств. Для любой борелевской меры $p\in P(X)$ задается внешняя мера $p^*(E)=\inf\{p(B):B\supseteq E,\; B\in B_X\}$ и пополненная $\sigma$-алгебра $B_X(p)=\{E\subseteq X:p^*(E)+p^*(E^c)=1\}$. Тогда $U_X=\bigcap_{p\in P(X)}B_X(p)$. Известно, что $B_X\subset A_X\subset U_X$, причем каждое из этих включений строгое, если $X$ - несчетное множество, [14]. Здесь символом $A_X$ обозначена $\sigma$-алгебра, порожденная аналитическими множествами [12]. В ограничениях (1.3) функции $h$ выбирались полуаналитическими из-за того факта, что проекции борелевских множеств не всегда будут борелевскими. В предположении 5.1 мы вынуждены перейти к универсально измеримым функциям, поскольку там фигурируют композиции аналитических и борелевских функций. Отметим,что переход к универсальной измеримости не затрудняет вычисление вероятностей и интегралов по вероятностным мерам, [8].

Приступим к обсуждению предположения 5.1. Во-первых, оно позволяет описывать случайные информационные множества рекуррентным образом. Действительно, из равенства (3.5) в условиях предположения 5.1 вытекает соотношение

$$\begin{array}{c}X_t(y^t,\xi^t)=f(g^{-1}_{\xi_t}(y_t)\cap\over... ...^t_{t-1} ,\kappa _{t-1}),\\ [1ex]\quad t\in 2\!:\!N,\end{array}$$ (5.3)

откуда, используя равенства (5.2) и включения для сигнала

$$y_1\in g(\mathcal{H}_1(\xi_1),\xi_1),\ \ \ \ y_{t+1}\in G(y_t,\xi^{t+1}_t,\kappa _t),\ \ \ \quad t\ge 1,$$ (5.4)

заключаем, что множества (3.2), (3.4) однозначно зависят от семейства марковских нестационарных частично наблюдаемых последовательностей $\{y^t_{t-1},\xi^t_{t-1},\kappa _{t-1}\},\quad t\in 2\!:\!N$. Нестационарность этой последовательности заключается в том, что на каждом шаге во включениях (5.4) равенство

$$y_1=g_1(\xi_1),\quad y_t=g_t(y_{t-1},\xi^t_{t-1},\kappa _{t-1}),\quad t\in 2\!:\!N,$$

может реализоваться на любом из селекторов $g_1(\xi)\in g(\mathcal{H}_1(\xi),\xi)$, $\; g_t(y,\xi^2$, $\kappa )\in G(y,\xi^2,\kappa )$, $t\in 2\!:\!N$. Теперь, исследовав свойства упомянутой частично наблюдаемой последовательности, можно реально описать семейство распределений для какой-либо функции от множества (5.3), например, функции расстояния $d(x,X_t(y^t,\xi^t))$ от произвольной точки $x\in X$ до этого множества.

Во-вторых, следует отметить, что, хотя множества (3.2), (3.4) и были ранее рекуррентно представлены через функции $W_t$ в общем случае, для этих функций затруднительно подобрать подходящее функциональное пространство так, чтобы функции или множества, описываемые ими, интерпретировались как точки в искомом пространстве. Поэтому в предположении 5.1 и возникла гипотеза о существовании пространства $K$. Ниже будут описаны некоторые классы систем, для которых упомянутое предположение выполняется.

В-третьих, предположение 5.1 по существу сводит ситуацию подсчета множеств информационной надежности к той, которая уже рассматривалась в примерах 3.9 и 4.4. Вычисления, которые при этом возникают, следует выполнять аналогично.

Рассмотрим их подробнее. Распределение пары $(\xi_2,\kappa _2)$ при заданных элементах $y^2,\xi_1,\kappa _1$ обозначим через $p_k(d\xi_2d\kappa _2\vert y^2,\xi_1,\kappa _1)$. На прямоугольниках $AC,\; A\in B_{\Xi},\; C\in B_K$ эта мера равна

$$p_k(AC\vert y^2,\xi_1,\kappa _1)=P_{\Xi}(A\cap k^{-1}_{y^2,\xi_1,\kappa _1}(C)).$$ (5.5)

Понятно, что распределение пары $(\xi_t,\kappa _t)$ при заданных элементах $y^t_{t-1}$, $\xi_{t-1}$, $\kappa _{t-1},\; t\in 2\!:\!N,$ имеет вид $p_k(d\xi_td\kappa _t\vert y^t_{t-1},\xi_{t-1},\kappa _{t-1})$, аналогичный (5.5). Следовательно, учитывая (5.3), множество информационной надежности в момент $t$ можем записать как

$$\begin{array}{c}\overline{X}_t(y^t,\alpha ) =\{x_t:P\{x_t\in... ... \vert y^{t-1}_{t-2},\xi_{t-2},\kappa _{t-2})\ldots \end{array}$$

$$\ldots p_k(d\xi_2d\kappa _2\vert y^2,\xi_1,\kappa _1)p_1(d\xi_1d\kappa _1\vert y_1)\ge\alpha \},\quad t\in 2\!:\!N,$$ (5.6)

где $p_1(AC\vert y_1)=P_{\Xi}(A\cap k^{-1}_{1y_1}(C))$. Согласно определению множества (4.1) мы должны помимо вероятности в формуле (5.6) подсчитать также вероятность

$$\begin{array}{c} P\{y_t\in G(y_{t-1},\xi_{t-1}^t,\kappa _{t-1... ... p_1(d\xi_1d\kappa _1\vert y_1),\quad t\in 2\!:\!N. \end{array}$$ (5.7)

Отметим, что в каждой из формул (5.6), (5.7) $t-1$ интеграл.