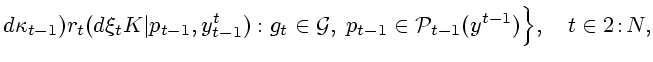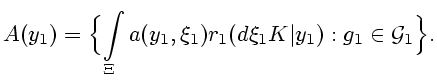

Next: 7 Некоторые классы статистически
Up: ANANIEV
Previous: 5 Построение множеств информационной
Как уже отмечалось выше в пункте 3,
множества информационной надежности теряют свой смысл в чисто
случайных системах. Однако при предположении 5.1, благодаря
рекуррентному характеру случайных множеств, возможно обобщить
процедуру фильтрации нелинейных систем так, чтобы она подходила
и для чисто случайных, и для чисто детерминированных систем. В
данном пункте считаем предположение 5.1 выполненным.
Случайным состоянием нашей системы в момент 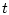 является
множество
является
множество
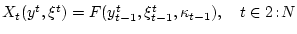 , согласно (5.3). Пусть
, согласно (5.3). Пусть
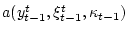 - некоторая числовая
функция от информационного множества, обладающая свойством
универсальной измеримости. В частности, таковой будет функция
расстояния
- некоторая числовая
функция от информационного множества, обладающая свойством
универсальной измеримости. В частности, таковой будет функция
расстояния
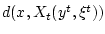 . Набор таких функций расстояния
при разных
. Набор таких функций расстояния
при разных  позволяет восстановить замыкание множества. Можно
рассмотреть также и опорную функцию [1,11], но тогда будет
восстановлена только выпуклая и замкнутая оболочка множества.
Конечно, в последнем случае предполагается, что пространство
позволяет восстановить замыкание множества. Можно
рассмотреть также и опорную функцию [1,11], но тогда будет
восстановлена только выпуклая и замкнутая оболочка множества.
Конечно, в последнем случае предполагается, что пространство 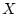 является линейным и локально выпуклым.
является линейным и локально выпуклым.
Итак, опишем вначале условные распределения для оценки неизвестной
функции
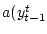 ,
,
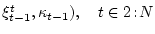 .
Пусть
.
Пусть 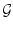 - это семейство селекторов многозначного
отображения (5.2), которое не пусто по предположению 5.1.
Аналогично,
- это семейство селекторов многозначного
отображения (5.2), которое не пусто по предположению 5.1.
Аналогично,
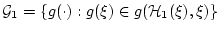 - семейство универсально измеримых
селекторов на первом шаге. Для выбранной последовательности
селекторов
- семейство универсально измеримых
селекторов на первом шаге. Для выбранной последовательности
селекторов
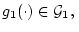
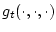
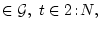 рассмотрим частично наблюдаемую
марковскую последовательность
рассмотрим частично наблюдаемую
марковскую последовательность
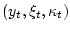 , порождаемую
уравнениями
, порождаемую
уравнениями
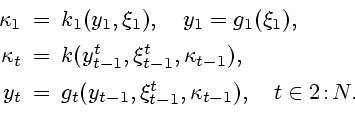 |
(6.1) |
Определим борелевское стохастическое ядро
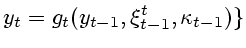 |
(6.2) |
на шаге
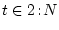 , которое однозначно продолжается на борелевскую
, которое однозначно продолжается на борелевскую
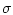 -алгебру
-алгебру
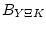 и задает распределение для
элемента
и задает распределение для
элемента
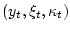 ,
,
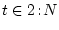 . На первом шаге имеем
безусловное распределение
. На первом шаге имеем
безусловное распределение
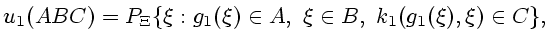 |
(6.3) |
которое так же, как и в пункте 2,
разложим по формуле
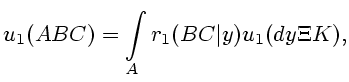 |
(6.4) |
где
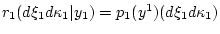 -
условное распределение ненаблюдаемых величин
-
условное распределение ненаблюдаемых величин
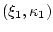 .
Образуем семейство
.
Образуем семейство
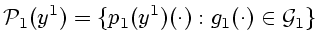 |
(6.5) |
всевозможных условных распределений на первом шаге. Далее
совершаем прогноз на второй шаг:
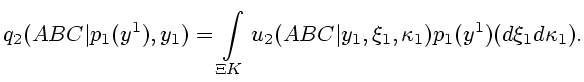 |
(6.6) |
Полученное распределение снова раскладываем:
где
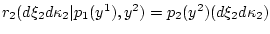 -
условная мера. Аналогично (6.5) образуем семейство
и так далее. На шаге
-
условная мера. Аналогично (6.5) образуем семейство
и так далее. На шаге
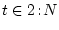 имеем
имеем
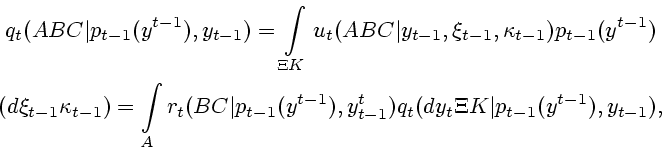 |
(6.7) |
где
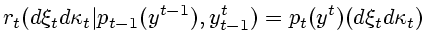 |
(6.8) |
- условное распределение ненаблюдаемых величин
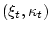 на шаге
на шаге 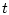 при заданном сигнале
при заданном сигнале 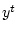 .
Соответствующее семейство этих распределений имеет вид
.
Соответствующее семейство этих распределений имеет вид
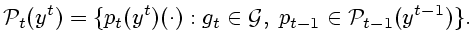 |
(6.9) |
Таким образом, формулы (6.2)-(6.9) описывают процедуру
построения условных распределений для ненаблюдаемых величин в
системе (6.1). В силу неопределенности, которая выражается
здесь включениями (5.4), мы получаем семейства условных
распределений (6.9). Ясно, что процедура, представленная в
настоящем пункте, дает единообразное решение задачи фильтрации,
охватывающее крайние случаи пункта 2 при условиях предположения
5.1. Оценкой неизвестной функции
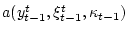 будем считать множество
условных средних
будем считать множество
условных средних
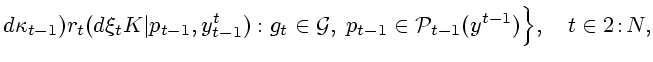 |
(6.10) |
из
которого можно получить уже конкретную точечную оценку неизвестной
функции, например, взять чебышевский центр этого числового
множества, то есть середину минимального отрезка, накрывающего
множество. На первом шаге равенство (6.10) принимает более
простой вид:
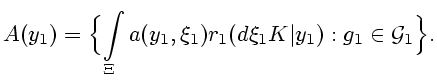 |
(6.11) |
Суммируем рассуждения
настоящего пункта в виде утверждения.
Теорема 6.1
Пусть выполнено предположение 5.1 и задана
числовая универсально измеримая функция
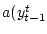 ,
,
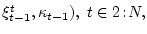 от случайного
информационного множества
от случайного
информационного множества (
5.3)
. Тогда множество
условных средних от указанной функции описывается равенством
(
6.10)
или (
6.11)
для первого шага. Условные
стохастические распределения в упомянутых соотношениях
определяются рекуррентными формулами (
6.2)-(
6.9)
и
являются универсально измеримыми.


Next: 7 Некоторые классы статистически
Up: ANANIEV
Previous: 5 Построение множеств информационной
2003-06-05
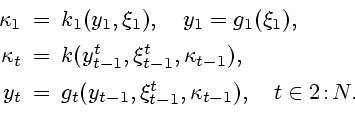
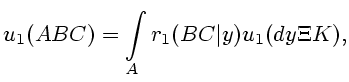
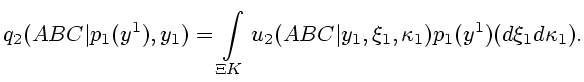
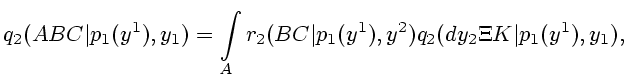
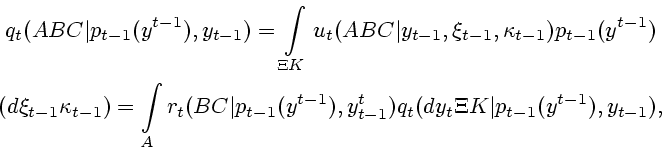
![$\displaystyle A(y^t)=\{M[a(y^t_{t-1},\xi^t_{t-1},\kappa _{t-1})
\vert y^t]\}=
\...
...Xi}\int\limits_{\Xi
K}a(y^t_{t-1},\xi^t_{t-1},\kappa _{t-1})p_{t-1}(d\xi_{t-1}
$](img278.gif)