

Next: 4 Условные множества информационной
Up: ANANIEV
Previous: 2 Решение задачи фильтрации
Перейдем к общему случаю систем вида
(1.1)-(1.3). Введем ряд новых понятий, обозначений и
примем
Это предположение обеспечивает непустоту множества
допустимых
траекторий для всякой реализации случайной
последовательности. Теперь по аналогии с детерминированным случаем
введем функции типа (2.3):
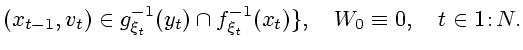 |
(3.1) |
Основные свойства этих функций содержатся в следующем
утверждении.
Лемма 3.2
Функции
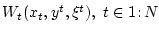 , заданные на
декартовом произведении
, заданные на
декартовом произведении 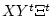 со значениями в
со значениями в
![$ [0,+\infty]$](img66.gif) , являются полуаналитическими снизу.
, являются полуаналитическими снизу.
Доказательство леммы аналогично рассуждению, проведенному в
теореме 2.2.
О п р е д е л е н и е 3.3. Пусть сигнал 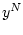 реализовался в
системе (1.1)-(1.3). Тогда случайным информационным
множеством в момент
реализовался в
системе (1.1)-(1.3). Тогда случайным информационным
множеством в момент 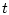 назовем совокупность
назовем совокупность
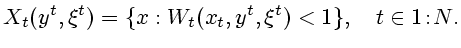 |
(3.2) |
В отличие от детерминированного случая множества (3.2)
могут быть пустыми. Необходимым и достаточным условием
непустоты информационных множеств будет включение
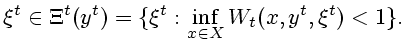 |
(3.3) |
Отметим также, что в
общем случае множества (3.2) нельзя назвать оценками,
поскольку они зависят от неизвестной реализации 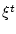 . Нам еще
потребуются множества допустимых неопределенных факторов на шаге
. Нам еще
потребуются множества допустимых неопределенных факторов на шаге
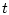 :
:
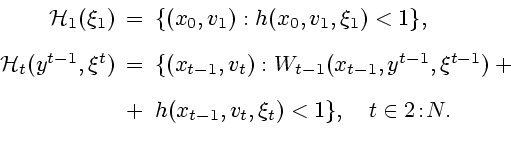 |
(3.4) |
Эти
множества на шаге 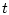 будут во всяком случае непустыми, если
выполнены включения (3.3). Связь введенных множеств изложена
в следующем утверждении.
будут во всяком случае непустыми, если
выполнены включения (3.3). Связь введенных множеств изложена
в следующем утверждении.
Теорема 3.4
Пусть выполнено предположение 3.1
и сигнал 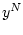 реализовался в системе
реализовался в системе (
1.1)-(
1.3)
. Тогда
множества (
3.2), (
3.4)
, непустые при выполнении
включения (
3.3)
, являются аналитическими. Кроме того,
имеем соотношения
Утверждение теоремы следует из леммы 3.1 и определений множеств
(3.2), (3.4). Отметим, что включение (3.6)
необходимо и достаточно для непустоты случайного информационного
множества на шаге 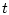 после реализации случайного элемента
после реализации случайного элемента
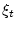 .
.
З а м е ч а н и е 3.5. Равенство (3.5) и включение (3.6), вообще
говоря, не рекуррентны. В случае геометрических ограничений,
когда
![$\displaystyle h(x,v,\xi)=\left\{\begin{array}{rl}0,&(x,v,\xi)\in\mathcal{W}, \\ [1ex]+\infty,&(x,v,\xi)\notin\mathcal{W},\end{array}\right.$](img125.gif) |
(3.7) |
где
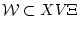 - аналитическое множество, можем
определить стационарные многозначные
отображения
- аналитическое множество, можем
определить стационарные многозначные
отображения
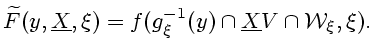 |
(3.8) |
Здесь
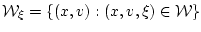 - сечение
множества
- сечение
множества 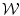 . Тогда имеем стационарные
соотношения
. Тогда имеем стационарные
соотношения
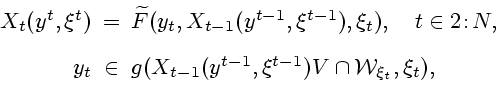 |
(3.9) |
причем в качестве начального можно выбирать любое множество 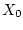 со свойством
со свойством
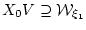 . Отметим, что здесь
множество допустимых неопределенных факторов
. Отметим, что здесь
множество допустимых неопределенных факторов
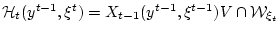 .
.
В статистически неопределенном случае имеет смысл ввести
О п р е д е л е н и е 3.6. Множеством информационной надежности назовем
совокупность
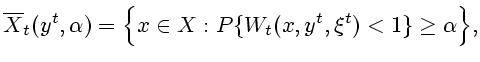 |
(3.10) |
где
![$ \alpha \in [0,1]$](img135.gif) и
вероятность подсчитывается согласно безусловному распределению
вектора
и
вероятность подсчитывается согласно безусловному распределению
вектора 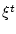 при зафиксированных элементах
при зафиксированных элементах 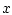 и
и 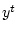 .
.
Приступая к обсуждению данного определения, отметим, что в чисто
случайных системах оно теряет свой смысл, а в детерминированных
сводится к известному, то есть
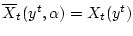 .
При некоторых числах
.
При некоторых числах 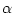 введенные множества могут быть пустыми.
Рассмотрим примеры построения множеств информационной надежности.
введенные множества могут быть пустыми.
Рассмотрим примеры построения множеств информационной надежности.
П р и м е р 3.7. Пусть на прямой задана одношаговая система
а
ограничения на неопределенные параметры имеют вид:
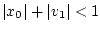 . Случайная величина
. Случайная величина 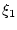 задана своей
функцией распределения
задана своей
функцией распределения 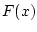 . Тогда ясно, что
. Тогда ясно, что
В частном случае,
когда 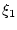 принимает два значения
принимает два значения 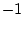 и
и 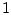 с равной
вероятностью
с равной
вероятностью 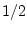 , имеем
, имеем
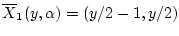 ,
если
,
если 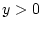 , и
, и
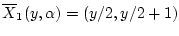 , если
, если 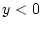 .
Данные равенства имеют место при
.
Данные равенства имеют место при
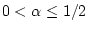 ; при
; при
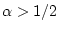 множества информационной надежности пусты.
множества информационной надежности пусты.
П р и м е р 3.8. Зададим одношаговую систему на прямой уравнениями
где неопределенный параметр
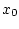 стеснен ограничением
стеснен ограничением
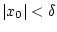 , а независимые случайные
величины
, а независимые случайные
величины 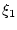 и
и 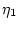 заданы своими функциями
распределения
заданы своими функциями
распределения 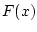 и
и 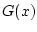 соответственно. Задача нахождения
информационного множества сводится тогда к подсчету вероятности
события
соответственно. Задача нахождения
информационного множества сводится тогда к подсчету вероятности
события
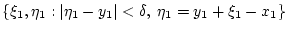 на плоскости переменных
на плоскости переменных
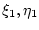 .
Эта вероятность равна
.
Эта вероятность равна
Отсюда получаем, что в случае,
когда хотя бы одна функция распределения 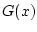 или
или 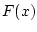 является непрерывной, указанные интегралы равны нулю и все
множества
является непрерывной, указанные интегралы равны нулю и все
множества
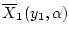 при
при 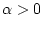 являются пустыми.
Впрочем, и в чисто случайной системе данного примера, когда
являются пустыми.
Впрочем, и в чисто случайной системе данного примера, когда
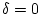 , условная мера
, условная мера
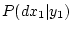 совпадает с безусловной, то
есть наблюдение не добавляет новой информации о неизвестном
элементе
совпадает с безусловной, то
есть наблюдение не добавляет новой информации о неизвестном
элементе 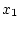 . Пусть, однако, случайные величины
. Пусть, однако, случайные величины
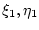 принимают два значения
принимают два значения 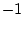 и
и 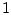 с равной вероятностью
с равной вероятностью 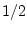 .
Тогда
.
Тогда
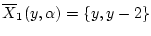 , если
, если 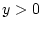 , и
, и
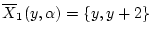 , если
, если 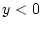 . Здесь
. Здесь
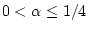 ; при
; при
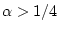 множества пусты.
множества пусты.
П р и м е р 3.9. Рассмотрим частный случай системы (1.1)-(1.3),
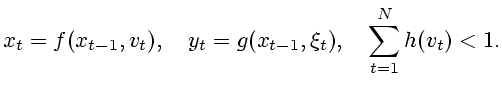 |
(3.11) |
Дополнительно предположим, что
уравнения в (3.11) однозначно разрешимы относительно 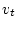 и
и
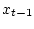 соответственно, то есть
соответственно, то есть
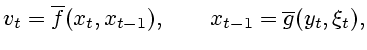 |
(3.12) |
где
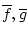 - борелевские функции. Тогда ясно,
что
- борелевские функции. Тогда ясно,
что
Отсюда имеем
где
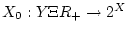 - стационарное
многозначное отображение. В то же время множества (3.4)
имеют здесь вид
где
- стационарное
многозначное отображение. В то же время множества (3.4)
имеют здесь вид
где
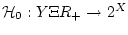 - стационарное многозначное отображение.
Распределение пары
- стационарное многозначное отображение.
Распределение пары
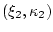 при заданном элементе
при заданном элементе 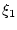 обозначим через
обозначим через
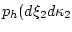
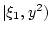 . На
прямоугольниках
. На
прямоугольниках
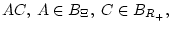 эта мера
равна
эта мера
равна
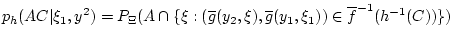 .
Понятно, что распределение пары
.
Понятно, что распределение пары
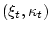 при заданных
элементах
при заданных
элементах
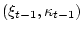 ,
, 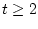 , имеет вид
, имеет вид
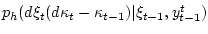 .
Следовательно, множество информационной надежности в момент
.
Следовательно, множество информационной надежности в момент 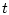 можно записать как
можно записать как
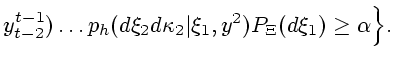 |
(3.13) |
Из последнего примера видно, что множества информационной
надежности не выражаются, вообще говоря, рекуррентно друг через
друга. Их вычисление проводится однотипно для всех 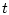 , но по
все возрастающему числу параметров. Это возможно сделать заранее
при небольшом числе шагов. Подсчитав заранее все необходимые
функции, для нахождения множеств остается лишь подставлять
результаты замеров.
, но по
все возрастающему числу параметров. Это возможно сделать заранее
при небольшом числе шагов. Подсчитав заранее все необходимые
функции, для нахождения множеств остается лишь подставлять
результаты замеров.


Next: 4 Условные множества информационной
Up: ANANIEV
Previous: 2 Решение задачи фильтрации
2003-06-05
![]() реализовался в
системе (1.1)-(1.3). Тогда случайным информационным
множеством в момент
реализовался в
системе (1.1)-(1.3). Тогда случайным информационным
множеством в момент ![]() назовем совокупность
назовем совокупность ![]() .
При некоторых числах
.
При некоторых числах ![]() введенные множества могут быть пустыми.
Рассмотрим примеры построения множеств информационной надежности.
введенные множества могут быть пустыми.
Рассмотрим примеры построения множеств информационной надежности.
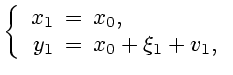
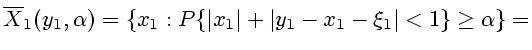
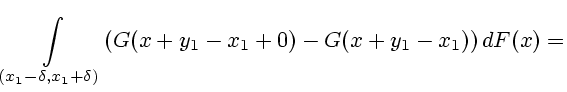
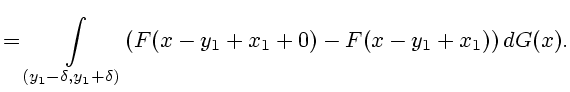
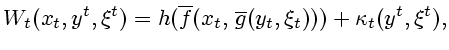
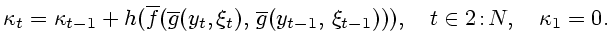
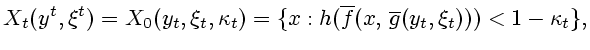
![\begin{displaymath}
\begin{array}{rcl}
\mathcal{H}_1\!\!\!&=&\!\!\!X\{v:h(v)<1\}...
...+h(v_{t+1})<\\ [1ex]
&&<1-\kappa _t\},\quad t\ge 1,
\end{array}\end{displaymath}](img177.gif)
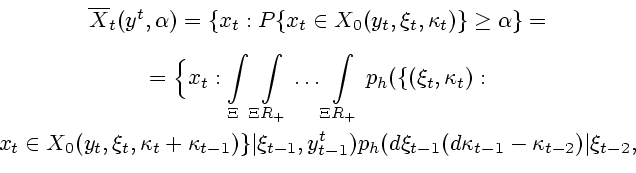
![]() , но по
все возрастающему числу параметров. Это возможно сделать заранее
при небольшом числе шагов. Подсчитав заранее все необходимые
функции, для нахождения множеств остается лишь подставлять
результаты замеров.
, но по
все возрастающему числу параметров. Это возможно сделать заранее
при небольшом числе шагов. Подсчитав заранее все необходимые
функции, для нахождения множеств остается лишь подставлять
результаты замеров.