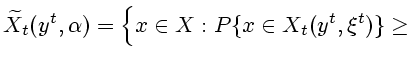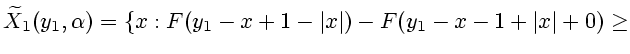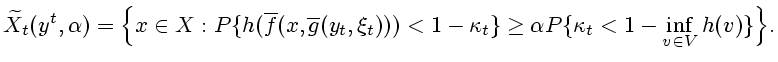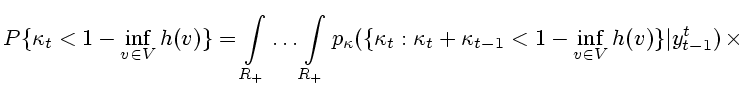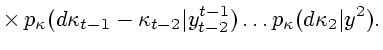

Next: 5 Построение множеств информационной
Up: ANANIEV
Previous: 3 Случайные информационные множества
Рассуждения
предыдущего пункта показывают, что множества (3.10) в
определенной мере дают представление о степени совместимости
принадлежащих им элементов с проведенными измерениями 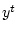 . Эту
степень можно в определенном смысле увеличить, если ввести более
широкие, чем (3.10), множества.
. Эту
степень можно в определенном смысле увеличить, если ввести более
широкие, чем (3.10), множества.
О п р е д е л е н и е 4.1. Условным множеством информационной надежности назовем
совокупность
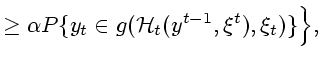 |
(4.1) |
где
![$ \alpha \in [0,1]$](img135.gif) и вероятность подсчитывается согласно безусловному
распределению вектора
и вероятность подсчитывается согласно безусловному
распределению вектора 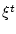 при зафиксированных элементах
при зафиксированных элементах 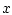 и
и 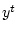 .
.
Ясно, что выполняется включение
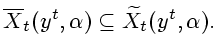 |
(4.2) |
Поэтому, если
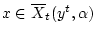 , то всегда
, то всегда
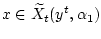 , где
, где
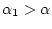 , в том
случае, когда параметр
, в том
случае, когда параметр 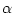 в (4.1) умножается на
ненулевую вероятность. Обсудим новое понятие на примерах
предыдущего пункта.
в (4.1) умножается на
ненулевую вероятность. Обсудим новое понятие на примерах
предыдущего пункта.
П р и м е р 4.2.
Рассмотрим систему примера 3.7. Имеем равенство
и
вероятность данного события равна
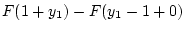 .
Следовательно,
.
Следовательно,
В частном случае, когда
величина 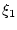 принимает два значения
принимает два значения 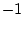 и
и 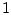 с равной
вероятностью
с равной
вероятностью 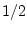 , имеем
, имеем
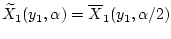 . Данные
равенства имеют место при
. Данные
равенства имеют место при
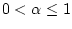 . Таким образом, в этом
частном случае условные множества информационной надежности не
пусты при всех
. Таким образом, в этом
частном случае условные множества информационной надежности не
пусты при всех 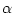 .
.
П р и м е р 4.3. Для системы примера 3.8 получаем равенство
и вероятность этого события равна
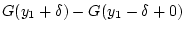 .
Здесь, по-прежнему, все множества
.
Здесь, по-прежнему, все множества
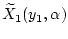 будут пустыми, если хотя бы одна из функций
будут пустыми, если хотя бы одна из функций 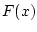 или
или 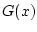 будет непрерывной. В случае, когда величины
будет непрерывной. В случае, когда величины
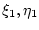 независимо принимают два значения
независимо принимают два значения 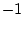 и
и 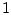 с равной
вероятностью
с равной
вероятностью 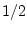 , имеем
, имеем
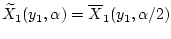 . Эти
множества не пусты при
. Эти
множества не пусты при
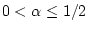 .
.
П р и м е р 4.4. Рассмотрим систему примера 3.9 с
предположениями (3.12). Тогда
Следовательно,
Вероятность в левой
части неравенства, определяющего данное множество, уже
подсчитана в примере 3.9. Распределение величины 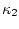 есть
мера
есть
мера
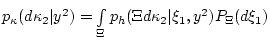 . Тогда распределение величины
. Тогда распределение величины
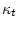 при заданном
при заданном
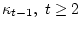 , имеет вид
, имеет вид
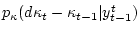 . Отсюда получаем
. Отсюда получаем
Для небольшого числа
шагов данная вероятность может быть подсчитана заранее.


Next: 5 Построение множеств информационной
Up: ANANIEV
Previous: 3 Случайные информационные множества
2003-06-05
![]() . Эту
степень можно в определенном смысле увеличить, если ввести более
широкие, чем (3.10), множества.
. Эту
степень можно в определенном смысле увеличить, если ввести более
широкие, чем (3.10), множества.