3. Оптимальные стратегии

Оптимальные стратегии, разрешающие задачи 1.1 и 1.2 для конфликтно-управляемых систем (1.1), будем строить в двух случаях, выделенных в параграфе 2. В первом случае будем полагать,что множества $P(t, y, \lambda)$ и $Q(t, z, \lambda)$, описывающие динамику, задаются равенствами

$$P(t,y,\lambda)=\{u \in R^n: u'P^{(1)}(t)u +\lambda f^{(1)}(t,y,u,\lambda) \le \mu^2 \},$$ (3.1)

$$Q(t,z,\lambda)=\{v \in R^n: v'Q^{(1)}(t)v +\lambda f^{(2)}(t,z,v,\lambda) \le \nu^2 \},$$ (3.2)

а матрицы $P^{(1)}(t), Q^{(1)}(t)$ и функции $f^{(1)}(t,y,u,\lambda), f^{(2)}(t,z,v,\lambda)$ удовлетворяют условиям 2.1(б) и 2.1(в).

Во втором случае будем полагать,что динамика объектов задается равенствами

$$\dot y = A^{(1)}(t)y + B^{(1)}(t)u + \lambda f^{(1)}(t, y, u, \lambda), u \in U = \{ u \in R^{m_1}: u'u \le \mu^2 \},$$ (3.3)

$$\dot z = A^{(2)}(t)z + B^{(2)}(t)v + \lambda f^{(2)}(t, z, v, \lambda), v \in V = \{ v \in R^{m_2}: v'v \le \nu^2 \},$$ (3.4)

а матрицы $A^{(i)}(t), B^{(i)}(t)$ и функции $f^{(i)}(t,z,v,\lambda), i=1,2$ удовлетворяют условиям 2.2(б), 2.2(в) и 2.2(г).

Будем предполагать, что функция $\sigma (x)$, описывающая плату игры, удовлетворяет следующему условию.

Условие 3.1. Функция $\sigma (x) \ge 0$ выпукла и удовлетворяет глобальному условию Коши-Липшица в $R^n.$

При выполнении условия 3.1 справедливо следующее равенство
[5, стр. 130]

$$\sigma (x) = \max_{l \in L} {[l'x - \omega (l)]},$$

$$\omega (l)=\sup_{x \in R^n}\{l'x - \sigma (x)\},\quad L=\mathrm{dom} \; \omega (l)=\{l \in R^n: \omega (l)< \infty \},$$

где $\omega (l)$ - функция, сопряженная к выпуклой функции $\sigma (x)$.

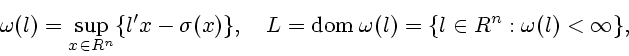
Введем в рассмотрение величину программного максимина [1,2]

$$\varepsilon^0(\vartheta, t, y, z, \lambda) = \max_{z(\varthe... ...(\vartheta ,\lambda) - l'y(\vartheta ,\lambda) - \omega (l)\}.$$

Области достижимости $G_1 = G_1(\vartheta, t, y, \lambda)$ и $G_2 = G_2(\vartheta, t, z, \lambda)$ объектов при каждом $\lambda \in \Lambda$ выпуклы замкнуты и ограничены, сопряженная функция выпукла, поэтому на основании общей теоремы о минимаксе мы можем записать

$$\varepsilon^0(\vartheta, t, y, z, \lambda) = \max_{l \in L} ... ...\lambda] -\rho_1 [l, \vartheta, t, y, \lambda] - \omega (l)\}.$$ (3.5)

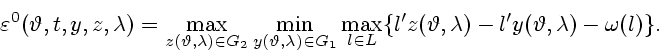
Будем предполагать, что игра регулярна [1-5], т.е. выполнено следующее условие.

Условие 3.2. Функция $\sigma (x)$ такова, что существует такая достаточно малая величина $\lambda^0(\Gamma) > 0$, что максимум в правой части равенства (3.5) достигается на единственном векторе $l^0 = l^0(\vartheta, t, y, z, \lambda) \in L$ для всех позиций $\{t, y, z\}$, для которых $t < \vartheta, \varepsilon^0 (\vartheta, t, y, z, \lambda) > 0$ при $\lambda \in \Lambda = \{\lambda: \vert \lambda \vert \le \lambda^0(\Gamma) \}$. Вектор-функция $l^0(\vartheta, t,y,z,\lambda)$ непрерывна по $t \in T$ и аналитична по переменным $y, z, \lambda)$ в области $\Gamma \times \Gamma \times \Lambda$.

Приведем примеры, когда выполнено условие 3.2. Для этого рассмотрим игры сближения-уклонения, в которых плата равна евклидовой норме вектора $x(\vartheta)$, т.е. $\sigma (x(\vartheta)) = \parallel x(\vartheta) \parallel$. Тогда $L = S$, $\omega (l) = 0$ при $l \in L$, и программный максимин (3.5) определяется равенством

$$\varepsilon^0 (\vartheta, t, y, z, \lambda)=\max_{l \in S} \... ...heta, t, z, \lambda] - \rho_1 [l, \vartheta, t, y, \lambda]\}.$$ (3.6)

Условие 3.2 для программного максимина (3.6) будет выполнено, если объекты однотипны, т.е. если $P^{(1)}(t) = Q^{(1)}(t)$ и $\mu - \nu \ge \delta > 0$ в первом случае и если $A^{(1)}(t)=A^{(2)}(t), B^{(1)}(t)=B^{(2)}(t)$ и $\mu - \nu \ge \delta > 0$ во втором случае. Требование $\mu - \nu \ge \delta > 0$ существенно. В статье [13] приведен пример, показывающий, что регулярность, имеющая место в случае линейных однотипных объектов при $\mu=\nu$, отсутствует за счет подходящего выбора нелинейных членов при любых сколь угодно малых значениях
параметра $\lambda$.

Если условие 3.2 выполнено, то решение экстремальной задачи (3.5) будем искать в виде ряда по степеням параметра $\lambda$

$$l^0(\vartheta, t, y, z, \lambda) = l^{(0)}(\vartheta, t, y, z) + \sum_{k=1}^\infty \lambda^k l^{(k)} (\vartheta, t, y, z).$$

Здесь вектор $l^{(0)}(\vartheta, t, y, z)$ есть решение экстремальной задачи (3.5) при $\lambda = 0.$

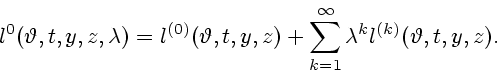
Введем в рассмотрение экстремальные стратегии [1-5].

О п р е д е л е н и е 3.1. Стратегии $U_e$ и $V_e$ называются экстремальными, если в каждой позиции $\{t, y, z\},$ для которой при $\lambda \in \Lambda,$ $\varepsilon^0(\vartheta, t, y, z, \lambda) > 0, t < \vartheta$, они определяются множествами $U_e^*(\vartheta, t, y, z, \lambda), V_e^*(\vartheta, t, y, z, \lambda),$ состоящими из всех тех векторов $u_e$ и $v_e$, которые удовлетворяют условиям максимума

$$u'_e {{\partial \rho_1 [l^0(\vartheta, t, y, z, \lambda), t,... ...vartheta, t, y, z,\lambda), t, y, \lambda] \over \partial y}},$$

$$v'_e{{\partial \rho_2 [l^0(\vartheta, t, y, z,\lambda), t, z... ...\vartheta, t, y, z,\lambda), t, z, \lambda]\over \partial z}}.$$

В других случаях множества $U_e^*, V_e^*$ выбираются произвольно.

В регулярном случае экстремальные стратегии $U_e$ и $V_e$ являются допустимыми. Опираясь на методы работ [1,3,4,10] и теорему 1, можно убедиться в справедливости следующего утверждения.

Теорема 3.1 Пусть динамика конфликтно управляемых систем описывается уравнениями $(\ref{s11})$, $(\ref{s31})$, $(\ref {s32})$ или $(\ref{s11})$, $(\ref {s33})$, $(\ref {s34})$, удовлетворяющими условиям $2.1$ или $2.2$, и пусть плата игры удовлетворяет условию $3.1$. Тогда в регулярном случае экстремальные стратегии $U_e$ и $V_e$ разрешают задачи $1.1$ и $1.2$ соответственно. Пара стратегий $\{U_e, V_e \}$ составляет седловую точку игры, причем цена игры $c(\vartheta, t, y, z, \lambda)$ совпадает с программным максимином, т.е. $c(\vartheta, t, y, z, \lambda) = \varepsilon^0 (\vartheta, t, y, z, \lambda)$, непрерывна по $t \in T$, аналитична по $\{y, z, \lambda \} \in \Gamma \times \Gamma \times \Lambda$ в области $t < \vartheta, \varepsilon^0 (\vartheta, t, y, z, \lambda) > 0$ и удовлетворяет уравнению Гамильтона - Якоби при условии $c(\vartheta, \vartheta, y, z, \lambda) = \sigma (y - z).$