В этом параграфе приводятся модельные примеры, в которых выполнены условия теоремы 3.1. Сначала дается пример, в котором динамика управляемого процесса удовлетворяет требованиям условия 2.1. Такие ситуации типичны, когда совпадают размерности управляющей силы и фазовых координат, или, наряду с ограничениями на управляющие силы, имеются также ограничения на скорости изменения фазовых координат управляемого процесса. Затем приводится пример, в котором динамика удовлетворяет требованиям условия 2.2. После этого формулируются игровые задачи о сближении объектов с аналогичной динамикой, в которых имеет место регулярный случай. Во втором примере даются результаты вычисления опорной функции области достижимости и оптимальных стратегий игроков.
П р и м е р 4.1. Рассмотрим задачу об управлении
вращением свободного абсолютно
твердого симметричного тела вокруг его центра тяжести в безвоздушном
пространстве. Пусть ![]() - главные центральные моменты инерции
тела, причем
- главные центральные моменты инерции
тела, причем ![]() и
и
![]() - достаточно малая величина.
Величины
- достаточно малая величина.
Величины
![]() означают управляющие моменты, создаваемые
двигателями относительно главных центральных осей инерции. Обозначив
через
означают управляющие моменты, создаваемые
двигателями относительно главных центральных осей инерции. Обозначив
через ![]() проекции вектора угловой скорости вращения тела на
глвные центральные оси инерции, запишем динамические уравнения Эйлера
проекции вектора угловой скорости вращения тела на
глвные центральные оси инерции, запишем динамические уравнения Эйлера
П р и м е р 4.2. Рассмотрим материальную
точку ![]() переменной массы
переменной массы ![]() , движущуюся
по идеально гладкой горизонтальной плоскости
, движущуюся
по идеально гладкой горизонтальной плоскости ![]() под действием заданной
силы притяжения (отталкивания) к началу координат
под действием заданной
силы притяжения (отталкивания) к началу координат
![]() , где
, где ![]() - некоторая малая
постоянная. Реактивная масса выбрасывается с постоянной по величине
относительной скоростью
- некоторая малая
постоянная. Реактивная масса выбрасывается с постоянной по величине
относительной скоростью ![]() . Проектируя уравнение Мещерского на оси
координат
. Проектируя уравнение Мещерского на оси
координат ![]() и
и ![]() , получим следующие уравнения движения точки
, получим следующие уравнения движения точки ![]()
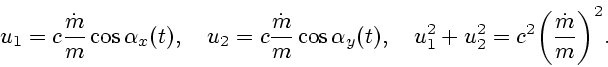
Пусть на управления наложено ограничение
![]() .
Для системы (4.2) вычислим опорную функцию
.
Для системы (4.2) вычислим опорную функцию
![]() сечения области
достижимости
сечения области
достижимости
![]() плоскостью
плоскостью
![]() Это значит, что описанные выше вычисления следует вести
при условии, что вектор
Это значит, что описанные выше вычисления следует вести
при условии, что вектор ![]() имеет вид
имеет вид
![]() Вектор-функция
Вектор-функция
![]() (2.4)
имеет вид
(2.4)
имеет вид
Отметим, что условие 2.2(в) существенно. Опорная функция области
достижимости системы (4.2) в пространстве
![]() при
при ![]() определяется равенством
определяется равенством
![\begin{displaymath}
+ \zeta \int\limits_t^\vartheta \sqrt
{[l_1(\vartheta - \tau) + l_2 ]^2 +
[l_3(\vartheta - \tau) + l_4 ]^2}d\tau.
\end{displaymath}](img218.gif)
П р и м е р 4.3. Рассмотрим задачу выравнивания
угловых скоростей
двух симметричных тел вращающихся вокруг
центров тяжести в пространстве перед стыковкой,
когда тело, с которым необходимо состыковаться, вращается под действием
неизвестной ограниченной помехи.
Пусть ![]() и
и ![]() - проекции векторов угловой
скорости вра- щения тел на главные центральные оси инерции,
- проекции векторов угловой
скорости вра- щения тел на главные центральные оси инерции,
![]() и
и ![]() - главные моменты внешних сил,
- главные моменты внешних сил,
![]() и
и
![]() - моменты инерции
относительно этих осей первого и второго тела соответственно.
Предположим, что достаточно малы величины
- моменты инерции
относительно этих осей первого и второго тела соответственно.
Предположим, что достаточно малы величины
![]() и
и
![]() .
В соответствии с (4.1) движения тел вокруг центров тяжести
происходят по законам
.
В соответствии с (4.1) движения тел вокруг центров тяжести
происходят по законам
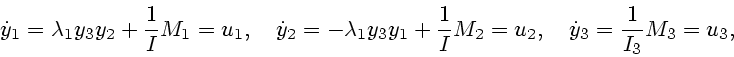
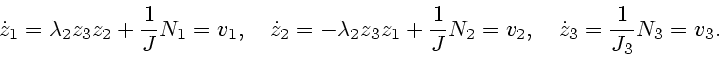
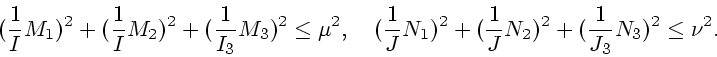
При ![]() объекты однотипны, следовательно, при
объекты однотипны, следовательно, при
![]() будет иметь место регулярный случай и для
вычисления экстремальных стратегий игроков можно использовать
результаты теоремы 3.1.
будет иметь место регулярный случай и для
вычисления экстремальных стратегий игроков можно использовать
результаты теоремы 3.1.
П р и м е р 4.4. Рассмотрим задачу
сближения-уклонения двух точек ![]() и
и ![]() переменной
массы, движущихся по идеально гладкой горизонтальной плоскости
под действием заданной силы притяжения (отталкивания) к началу
координат. В соответствии с (4.2) движения точек происходят по
законам
переменной
массы, движущихся по идеально гладкой горизонтальной плоскости
под действием заданной силы притяжения (отталкивания) к началу
координат. В соответствии с (4.2) движения точек происходят по
законам
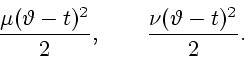
Величина программного максимина (3.5) определяется равенством
![\begin{eqnarray*}
\lefteqn{\varepsilon^0(\vartheta, t, y, z, \lambda)=} [2ex]...
...l_1^3+l_3^3)(\vartheta - t)^6 \over 120}\right]+ \dots
\right\}.
\end{eqnarray*}](img244.gif)
Вектор
![]() на котором
достигается максимум в правой части этого равенства, ищем в виде
на котором
достигается максимум в правой части этого равенства, ищем в виде
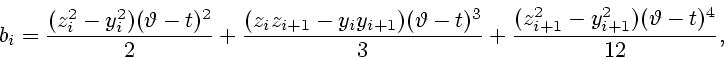
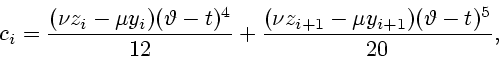
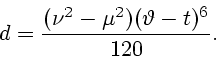
Определим экстремальные стратегии ![]() и
и ![]() игроков. В области
игроков. В области
![]() множества
множества ![]() и
и ![]() состоят
из единственной точки
состоят
из единственной точки
![\begin{displaymath}
u_{1e}=\mu l_1^{(0)} \left[ 1+\lambda \left({l_1^{(1)} \over l_1^{(0)}}+\beta_1
(l_3^{(0)})^2 \right)\right],
\end{displaymath}](img258.gif)
![\begin{displaymath}
u_{2e}=\mu l_3^{(0)} \left[ 1+\lambda \left({l_3^{(1)} \over l_3^{(0)}}-\beta_1
(l_1^{(0)})^2 \right)\right],
\end{displaymath}](img259.gif)
![\begin{displaymath}
v_{1e}=\nu l_1^{(0)} \left[ 1+\lambda \left({l_1^{(1)} \over l_1^{(0)}}+\beta_2
(l_3^{(0)})^2 \right)\right],
\end{displaymath}](img260.gif)
![\begin{displaymath}
v_{2e}=\nu l_3^{(0)} \left[ 1+\lambda \left({l_3^{(1)} \over l_3^{(0)}}-\beta_2
(l_1^{(0)})^2 \right)\right],
\end{displaymath}](img261.gif)
![\begin{displaymath}
\beta_1=(\vartheta - t)^2 \left[ {(y_1-y_3) \over 3}+
{(y_2-...
...
\mu {(l_1^{(0)}-l_3^{(0)})(\vartheta - t)^2 \over 20}\right],
\end{displaymath}](img262.gif)
![\begin{displaymath}
\beta_1=(\vartheta - t)^2 \left[ {(z_1-z_3) \over 3}+
{(z_2-...
...
\nu {(l_1^{(0)}-l_3^{(0)})(\vartheta - t)^2 \over 20}\right].
\end{displaymath}](img263.gif)
Поступила 05.08.99