2. Область достижимости

Рассмотрим управляемую систему

$$\dot x =w \in R(t,x,\lambda).$$ (2.1)

Будем полагать, что многозначное отображение $R(t, x, \lambda)$ удовлетворяет одному из следующих условий.

Условие 2.1.

(а) Множество $R(t, x, \lambda)$ имеет вид

$$R(t,x,\lambda)=\{w \in R^n: w'R^{(1)}(t)w+\lambda f(t, x, w, \lambda) \le \zeta^2 \}$$ (2.2)

(здесь и в дальнейшем штрих означает транспонирование).

(б) Матрица $R^{(1)}(t)$ определенно положительна и непрерывна по $t \in T.$

(в) Функция $f(t, x, w, \lambda)$ непрерывна по $t \in T$ и аналитична по всем остальным переменным.

Такие ситуации типичны, когда совпадают размерности управляющей силы и фазовых координат, или, наряду с ограничениями на управляющие силы, имеются также ограничения на скорости изменения всех фазовых координат управляемого процесса.

Условие 2.2.

(а) Множество $R(t, x, \lambda)$ имеет вид

$$\begin{array}{rcl} R(t,x,\lambda)\!\!\!&=&\!\!\!\{w \in R^n:... ...\{ {w^{*}} \in R^m: {w^{*}}'{w^{*}} \le \zeta^2 \}. \end{array}$$ (2.3)

(б) Матрицы $A(t) \in R^{nn}$ и $B(t) \in R^{nm}$ непрерывны по $t \in T,$ причем $2 \le m \le n$.

(в) Пусть $X[t, \tau]$ - фундаментальная матрица решений линейной однородной системы $\dot x = A(t)x$. Каков бы ни был единичный вектор $l \in R^n$, вектор-функция

$$g(l, \vartheta, \tau) = \{X[\vartheta, \tau]B(\tau)\}'l \in R^m$$

имеет вид

$$g(l, \vartheta, \tau)=\alpha (\vartheta, \tau)g^*(l, \vartheta, \tau),$$ (2.4)

где $\alpha (\vartheta, \tau)$ - скалярная функция, и $g^*(l, \vartheta, \tau)$ - ненулевой вектор при всех $\tau \in T.$

(г) Функция $f(t, x, w^{*}, \lambda)$ непрерывна по $t \in T$ и аналитична по всем остальным переменным.

При выполнении условия 2.1 (или 2.2) дифференциальное включение (2.1), (2.2) (или (2.1), (2.3)) для любой начальной позиции $\{t_0, x_0\}$ имеет при достаточно малых значениях параметра $\lambda$ множество $X[t_0, x_0, \lambda]$ решений $x(t, \lambda) = x(t;t_0, x_0, \lambda)$, определенных на любом заданном отрезке времени $T = [t_0, \vartheta].$

Сечение множества $X[t_0, x_0, \lambda]$ при $t = \vartheta$ будем называть областью достижимости системы (2.1) из состояния $x(t_0) = x_0$ к моменту времени $t = \vartheta$ и обозначать символом $G(\vartheta, t_0, x_0, \lambda).$ При условии 2.1 (или 2.2) и малых значениях $\lambda$ множество $G(\vartheta, t_0, x_0, \lambda)$ является строго выпуклым, замкнутым и ограниченным. Для построения решений задач 1.1 и 1.2 необходимо знать опорную функцию $\rho [l, \vartheta, t, x, \lambda]$ области достижимости $G(\vartheta, t, x, \lambda)$ при

$$l \in S =\{l \in R^n: l'l = 1\}.$$

В рассматриваемых ситуациях, описываемых условиями 2.1 и 2.2, для построения опорной функции удобно пользоваться методом динамического программирования.

Теорема 2.1. Пусть выполнено условие $2.1$ (или $2.2$), тогда опорная
функция $\rho [l, \vartheta, t, x, \lambda]$ области достижимости $G(\vartheta, t, x, \lambda)$ является непрерывной функцией времени и при каждом $t \in T$ аналитической функцией переменных $l, x, \lambda$ в области $S \times \Gamma \times \Lambda$, где $\Gamma$ - произвольное ограниченное множество в $R^n$ и $\Lambda$ - некоторая малая окрестность точки $\lambda = 0$.

Д о к а з а т е л ь с т в о. Проверим справедливость утверждения теоремы в случае, когда выполнено условие 2.1. При условии 2.2 доказательство проводится аналогично с несущественными изменениями.

Опорная функция $\rho [l, \vartheta, t, x, \lambda]$ является [10] решением задачи Коши

$$\frac{\partial \rho }{\partial t}+\max_{w \in R(t,x,\lambda)... ...x}=0, \quad \rho [l, \vartheta, x, \lambda]=l'x,\quad l \in S.$$ (2.5)

При $\lambda = 0$ задача (2.5) имеет решение

$$\rho^{(0)} [l, \vartheta, t, x]=l'x+ \zeta \int\limits_t^\vartheta(l'[R^{(1)}(\tau)]^{-1}l)^{1/2}d\tau.$$

Матрица $R^{(1)}(t)$ определенно положительна, поэтому максимум в левой части уравнения (2.5) достигается на единственном векторе

$$w^0(\vartheta, t, x, \lambda) = \zeta [R^{(1)}(t)]^{-1}\psi ... ... \psi)^{-1/2}+ \lambda w_1^0 (\psi, \vartheta, t, x, \lambda),$$

$$\psi ={\partial \rho [l, \vartheta, t, x, \lambda] \over \partial x},$$

где $w^0(\vartheta, t, x, \lambda)$ - вектор-функция непрерывная по $t$ и аналитическая по $l, x, \lambda$ в области $S \times \Gamma \times \Lambda$. При $\lambda \ne 0$ решение задачи (2.5) будем искать в виде

$$\rho [l, \vartheta, t, x, \lambda] = \rho^{(0)} [l, \vartheta, t, x] + \lambda \varkappa [l, \vartheta, t, x, \lambda].$$

Функцию $\varkappa [l, \vartheta, t, x, \lambda]$ надлежит искать как решение уравнения

$$\lambda \frac{\partial \varkappa}{\partial t} - \zeta (l'[R^... ...\frac{\partial \varkappa } {\partial x }\bigg )\bigg ]^{1/2} +$$

$$+\lambda \bigg (l + \lambda \frac{\partial \varkappa} {\part... ...artial \varkappa} {\partial x}, \vartheta, t, x, \lambda) = 0,$$

при условии $\varkappa [l, \vartheta, \vartheta, x, \lambda] = 0.$

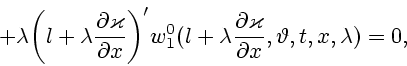
Квадратичная форма $l'[R^{(1)}(t)]^{-1}l \ne 0$ при всех $l \in S$ и $t \in T$, поэтому для произвольной ограниченной области $\Gamma \subset R^n$ можно указать достаточно малую величину $\lambda^0(\Gamma) > 0$ такую, что функция $\varkappa [l, \vartheta, t, x, \lambda]$ будет аналитической по $l \in S, x \in \Gamma$ и $\lambda$ при достаточно малых значениях $\lambda \in \Lambda = \{\lambda: \vert \lambda \vert \le \lambda^0(\Gamma) \}$, что и доказывает справедливость теоремы.

Таким образом, при $(l, t, x, \lambda) \in S\times T \times \Gamma \times \Lambda$ опорную функцию можно искать в виде сходящегося ряда

$$\rho [l, \vartheta, t, x, \lambda] = \rho^{(0)} [l, \varthet... ...m_{k=1}^\infty \lambda^k \varkappa^{(k)} [l, \vartheta, t, x].$$

Такой подход удобен тем, что нам всегда известно явное выражение функции $\rho^{(0)} [l, \vartheta, t, x]$, а для вычисления функций $\varkappa^{(k)} [l, \vartheta, t, x]$ при $k = 1, 2, \dots$ необходимо найти решение задач Коши для рекуррентной последовательности линейных дифференциальных уравнений в частных производных первого порядка.

Отметим, что в случае, когда размерность управляющей силы меньше, чем размерность фазового вектора, теорема 2.1, вообще говоря, неверна. В статье [12] приведены примеры, когда функция $\rho^{(0)} [l, \vartheta, t, x]$ недифференцируема по $l$. В таких ситуациях условия 2.2(б) и 2.2(в) оказываются существенными. Существенными являются и требования 2.1(а), 2.2(б). Если опорная гиперплоскость имеет касание с границей области управления более высокого порядка, чем первый, то опорная функция области управления недифференцируема по $l$ и, следовательно, теорема 2.1 также, вообще говоря, неверна.