где
где
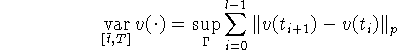
(точная верхняя грань берется по всем конечным разбиениям
Пусть движение объекта управления описывается системой
дифференциальных уравнений
![]()
где ![]() - соответственно n- и m-мерныe
функции времени;
f(t,x,v) - n-мерная вектор-функция;
B(t,x,v) -
- соответственно n- и m-мерныe
функции времени;
f(t,x,v) - n-мерная вектор-функция;
B(t,x,v) - ![]() -матрица-функция;
-матрица-функция;
![]() Производные в (1.1) следует понимать в обобщенном смысле
[2].
Пусть
Производные в (1.1) следует понимать в обобщенном смысле
[2].
Пусть ![]() ; определим множество
; определим множество
![]()
где ![]() - банахово пространство m-мерных функций
ограниченной вариации,
- банахово пространство m-мерных функций
ограниченной вариации,
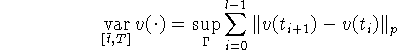
(точная верхняя грань берется по всем конечным разбиениям
![]() отрезка
отрезка ![]() - p-норма вектора v.
Назовем
- p-норма вектора v.
Назовем ![]() множеством допустимых управлений.
множеством допустимых управлений.
Заметим, что при ![]() выполняется включение
выполняется включение ![]() .
.
Пусть функции f(t,x,v) и B(t,x,v) удовлетворяют следующим
требованиям:
![]()
![]()
для всех ![]() Согласно [3, с. 155,], в этом случае множество допустимых траекторий
равномерно ограничено, т.е. для всех
Согласно [3, с. 155,], в этом случае множество допустимых траекторий
равномерно ограничено, т.е. для всех ![]() соответствующая траектория
соответствующая траектория ![]() принимает
значения в
принимает
значения в ![]() где Q - компакт.
где Q - компакт.
Условие (А). Пусть функции f(t,x,v) и B(t,x,v)
подчиняются требованиям (1.2),
(1.3) и являются непрерывными по совокупности
переменных (t,x,v) в области
![]() а матрица-функция
а матрица-функция
![]() обладает непрерывными частными
производными
обладает непрерывными частными
производными
![]() и
и
![]() по x и v
в той же области, и выполняется условие Фробениуса
по x и v
в той же области, и выполняется условие Фробениуса
![]()
![]()
Кроме того, пусть существует число K>0 такое, что
![]()
для всех ![]()
Под решением (1.1), соответствующим функции ограниченной
вариации v(t), будем, как и в [3, с. 148,],
понимать вектор-функцию ![]() ,
являющуюся поточечным пределом последовательности
,
являющуюся поточечным пределом последовательности
![]() , порожденной последовательностью абсолютно
непрерывных функций
, порожденной последовательностью абсолютно
непрерывных функций ![]() , сходящейся поточечно к функции
v(t), если x(t) не зависит от выбора последовательности
, сходящейся поточечно к функции
v(t), если x(t) не зависит от выбора последовательности
![]() .
.
Согласно [3, с. 164,], условие (А) является достаточным
для того, чтобы
для любого ![]() существовала
единственная траектория
существовала
единственная траектория ![]() определенная на
интервале
определенная на
интервале ![]() и удовлетворяющая уравнению
и удовлетворяющая уравнению
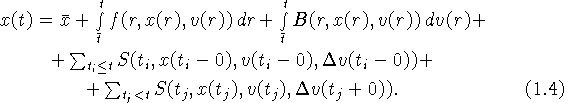
Здесь ![]() - непрерывная составляющая функции v(t);
второй интеграл в (1.4) - интеграл Римана-Стилтьеса
[4];
- непрерывная составляющая функции v(t);
второй интеграл в (1.4) - интеграл Римана-Стилтьеса
[4];
![]() - точки левого разрыва функции v(t);
- точки левого разрыва функции v(t);
![]() - точки правого разрыва функции v(t);
- точки правого разрыва функции v(t);
![]()
![]() а
функция
а
функция ![]() называемая
левым (правым) скачком функции x, определяется равенством
называемая
левым (правым) скачком функции x, определяется равенством
![]()
где z - решение задачи Коши
![]()
Сформулируем задачу оптимального управления:
требуется минимизировать функционал Больца
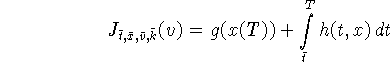
вдоль траекторий системы (1.1), где g и h -
скалярные функции, удовлетворяющие следующему условию.
Условие (Б).
Пусть функции g(x) и h(t,x)
непрерывны по всем своим переменным в области ![]() ,
,
![]() ; кроме того, пусть существует число K>0
такое, что
; кроме того, пусть существует число K>0
такое, что
![]()
для всех ![]()