3.1. Лемма о среднем значении функции 
на
отрезке со специальным весом.
Пусть 
- множество ненулевых, неотрицательных и интегрируемых
на 
функций. Будем называть эти функции весами.
Известно (см. стр. 1026, пункт 8.784 в [11]), что функция
при 
имеет
бесконечное множество нулей, все ее нули действительные и больше единицы.
Пусть n>0, обозначим через 
первый положительный нуль функции
т.е. положим
Определим функцию P на полуоси 
следующим образом
где 
- оператор сдвига с шагом (см. (2.8)) и
Из определения видно, что функция P является ненулевой,
неотрицательной и непрерывной на полуоси 
. Так как 
то по лемме 2.1 имеем 
т.е. 
при 
. Таким образом,
функция, определенная формулой (3.2), является весом
на отрезке 
, т.е. 
Справедливо следующее утверждение.
Лемма 3.1.
Пусть функция P определена формулой 
Тогда для
любого 
имеет место неравенство
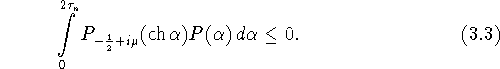
Д о к а з а т е л ь с т в опроведем по схеме,
разработанной в [12], [13], [3].
В силу замечания о компактности носителя P,
самосопряженности оператора 
, формулы умножения
(2.6), (2.8),
имеет место следующая цепочка равенств,
в которых используются обозначения (2.8)
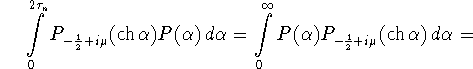
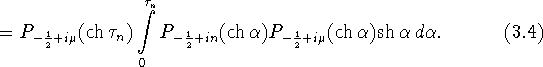
Вычислим последний интеграл. Для этого будем интегрировать его по
частям, используя дифференциальное уравнение, которому удовлетворяет
функция (см. [11, стр. 1012,])
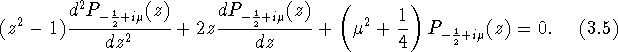
Известным способом (см. [10, стр. 31,]) это уравнение
преобразуем к уравнению без первой производной, именно
функция 
удовлетворяет
следующему уравнению
Запишем последний интеграл в (3.5) через функции
и вычислим его, используя (3.8)
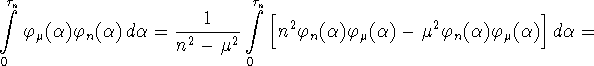
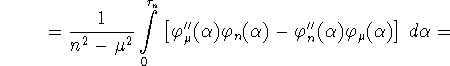
В результате, возвращаясь к функциям и
формуле (3.5), получаем
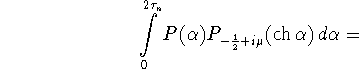
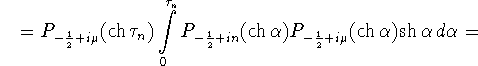
Так как 
(поскольку (см. [6],
[11]) 
все нули
вещественные, простые и при переходе
через точку функция меняет знак с "+" на "-"), то правая часть
последнего равенства неположительна при 
. Кроме того видно, что
правая часть первого равенства в (3.9) равна нулю при 
.
Лемма доказана.
3.2. Оценка сверху величины 
Теорема 3.1.
Пусть
Тогда справедливо неравенство
Д о к а з а т е л ь с т в о.
При 
выполняется неравенство 
.
Поэтому, для любой функции m из класса 
(см. (2.13)) имеем
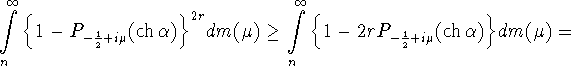
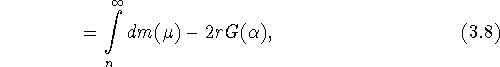
где
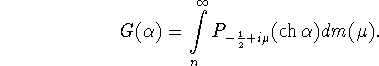
Из леммы 3.1 и неотрицательности меры 
следует неположительность среднего значения функции G
на отрезке с весом P, определенным формулой (3.2).
Действительно
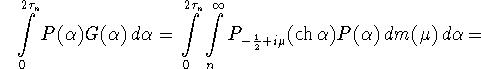
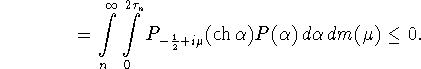
Поэтому в интервале 
найдется точка, в которой функция G
принимает неположительное значение. Отсюда и (3.8) получаем
неравенство
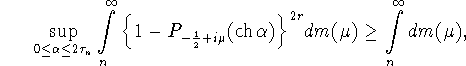
которое выполняется для любой функции m из класса , что вместе с
(2.11) и (2.13) влечет утверждение теоремы.
Таким образом, для величины 
справедлива следующая оценка
сверху
3.3. Оценка снизу величины
Применяя известную методику разработанную В.В.Арестовым [14, теорема 1,],
[3, лемма 4.2,], с учетом свойства (1.7), а также
известного свойства (см. фомулу (6) на стр. 4 в [15])
получаем такое утверждение.
Теорема 3.2.
Пусть 
тогда для любого 
и любого n>0
справедливо неравенство
3.4. Точные значения величин 
Напомним (см. (3.1)), что для n>0 через
мы обозначили первый положительный нуль функции Лежандра
.
Из теорем 3.1, 3.2 вытекает следующее утверждение.
Теорема 3.3.
Пусть 
.
Тогда на множестве всех функций
справедливо точное неравенство
Иными словами, имеет место равенство
Исходя из замечания § 2, пункта 3 о совпадении величин и
для величины 
получаем также
утверждение.
Теорема 3.4.
Пусть 
.
Тогда на множестве всех функций
справедливо точное неравенство
То есть выполняется равество
С помощью соображений аналогичных тем, которые применялись в работе
[3, Замечание 2.3,], нетрудно убедиться, что если
, 
то обе константы
и 
будут строго больше единицы.
Таким образом, наименьшее значение аргумента 
при котором константы и
выходят на свой минимум заключено между и 
Поступила 16.02.96