Наилучшее приближение в пространстве

1.1. Предварительные сведения об анализе Фурье на гиперболоиде. Пусть - псевдоевклидово пространство точек с билинейной формой

- полупсевдосфера в т.е. На существует метрика и мера, инвариантные относительно действия группы псевдовращений (см. [6]).

Пусть - пространство функций f, определенных на , таких, что

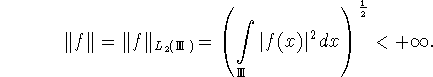
Аналог преобразования Фурье на и его обращение определяются следующим образом ([6], [7])



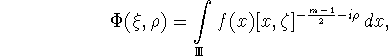
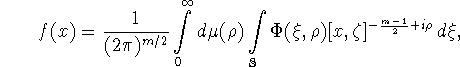
где - точка на единичной сфере в евклидовом пространстве - инвариантная относительно группы вращений на сфере мера,

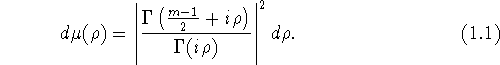
Справедлива формула Планшераля (см. [7])

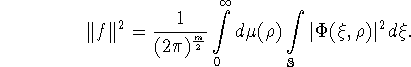
В дальнейшем мы будем использовать обозначение

где - присоединенная функция Лежандра (интегральное представление которой см. в [6]). И.В.Петрова получила следующие два утверждения (см. [4]).

Теорема 1.1. Для функций имеет место интегральное представление

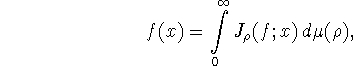
где определяется формулой , а

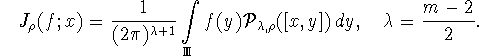
Теорема 1.2. Если оператор такой, что то

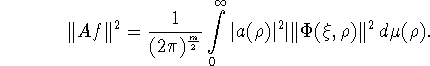
1.2. Аппарат приближения на гиперболоиде. Функцией с конечным спектром порядка n назовем такую функцию что для любого Через обозначим подпространство функций пространства с конечным спектром

а через обозначим наилучшее среднеквадратичное приближение функции f подпространством

Определим свертку функции с функцией равенством

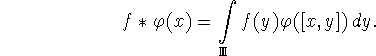
И.В.Петровой доказано следующее утверждение (см. [4]), в котором использовано стандартное обозначение характеристической функции множества B.

Теорема 1.3. Оператор задаваемый сверткой функции с ядром

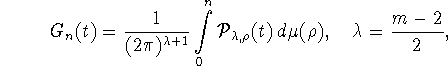
есть оператор проектирования на причем

Иными словами, справедлива формула



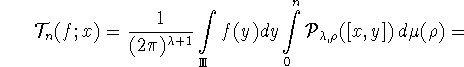
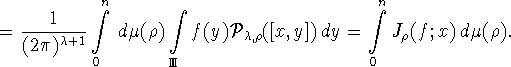
Из определения и теоремы 1.2, получаем

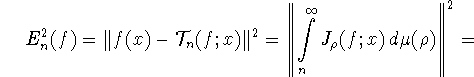
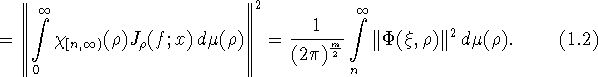
1.3. Модуль непрерывности на гиперболоиде. Назовем сдвигом функции f в точке x с шагом t выражение

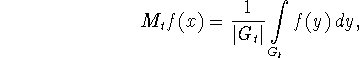
где - множество точек на гиперболоиде удаленных от точки x на гиперболическое расстояние - мера этого множества; dy - индуцированная мера на множестве (см. [4]).

Разность первого и высших порядков построим стандартным образом



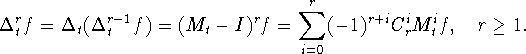
Здесь - тождественный оператор. Модуль непрерывности порядка функции в точке определим равенством

Так как величины и связаны соотношением (см. [4])

где

то для получаем выражение

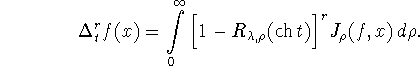
В силу теоремы 1.2 имеем

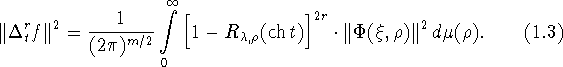
1.4. Экстремальная задача для точной константы в неравенстве Джексона - Стечкина в И.В.Петровой [4] установлено неравенство типа Джексона

с некоторой конечной константой Нас интересует наименьшая константа в этом неравенстве, точнее величина

Или, в силу формул (1.2) и (1.3),

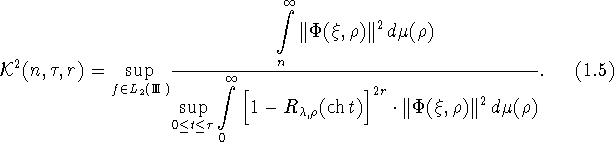
В случае, когда m=2, т.е. выражение (1.5) примет вид

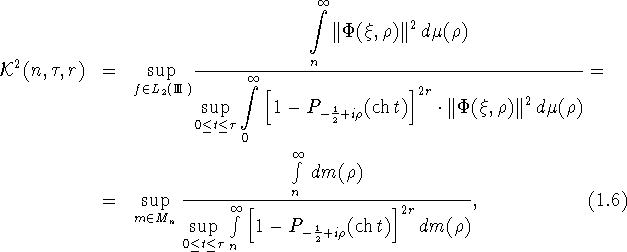
где

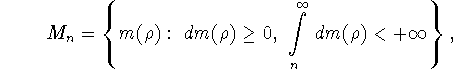
- функция Лежандра (см. [6]), которая как известно удовлетворяет неравенству

Это неравенство можно доказать, например, с помощью дифференциального уравнения (3.5) также как это сделано при доказательстве теоремы 7.3.1 на стр. 171 - 172 в монографии [10], а именно показать, что последовательность, образованная локальными максимумами функции и значением этой функции в точке t=0, является убывающей при .