Наилучшее приближение в пространстве

2.1. Предварительные сведения о преобразовании Мелера - Фока. Рассмотрим пространство комплексных функций вида со скалярным произведением и нормой

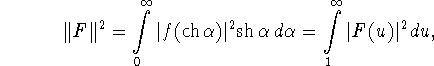
и пространство W функций для которых сходится интеграл

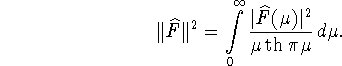
Как известно (см. [6, стр. 516,]) преобразование Мелера - Фока



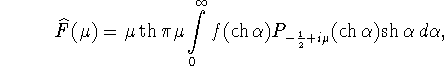
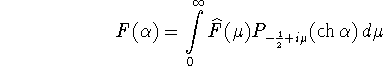
зада└т взаимно обратные отображения этих пространств друг на друга. При этом имеет место следующее равенство (см. [8])

а также справедливо соотношение ортогональности (см. [8])

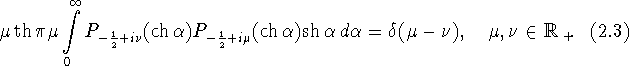
2.2. Наилучшее приближение в пространстве Пусть есть подпространство функций из , у которых преобразование Мелера - Фока имеет носитель на отрезке [0,n], т.е.

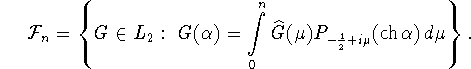
Наилучшее приближение функции подпространством определяется следующим образом

Для величины получим формулу, в которой использовано следующее обозначение

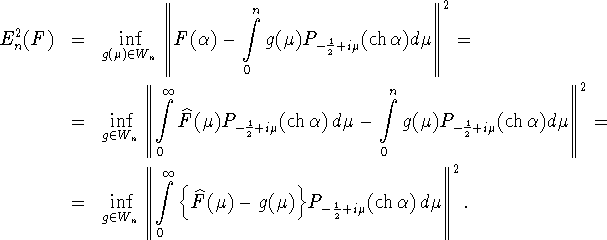
Применяя равенство (2.2) для величины получим формулу

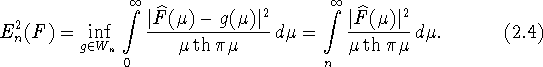
2.3. Оператор сдвига и модуль непрерывности в пространстве . Для функции определим обобщенный гиперболический сдвиг с шагом т.е. оператор действующий на функцию F по правилу

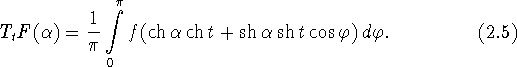
Как следует из результатов R.Takahashi (см. [10, гл. 1, п. 1,2,]), оператор самосопряжен относительно скалярного произведения (2.1). Кроме того, эта операция обладает следующим важным свойством (см. [6])

где

то есть, имеет место формула умножения для функции Лежандра

Нам понадобится еще одно свойство оператора сдвига , вытекающее из его определения.

Лемма 2.1. Пусть Функция непрерывна при всех и Тогда функция является непрерывной при всех и при

Д о к а з а т е л ь с т в о Непрерывность G очевидна. В силу определения (2.8), достаточно показать, что функция

принимает свои значения в полуинтервале , если

Действительно, в этом случае произведение положительно, поэтому выполняются соотношения

Лемма доказана.

Определим разностный оператор натурального порядка соответствующий сдвигу по формуле

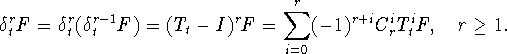
Здесь - тождественный оператор. Модулем непрерывности порядка r функции назовем величину

Получим выражение для . Из формулы умножения (2.8) следует, что

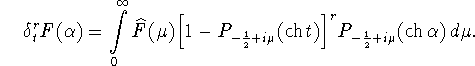
В силу (2.2) имеем

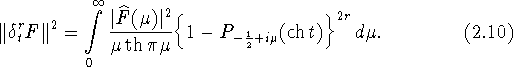
Таким образом, для величины имеет место следующее представление.

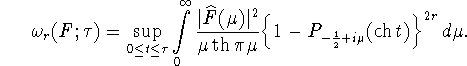
Из формул (2.6) и (2.11) видно, что задача о вычислении

точной константы в соответствующем неравенстве Джексона - Стечкина, сводится к следующей задаче

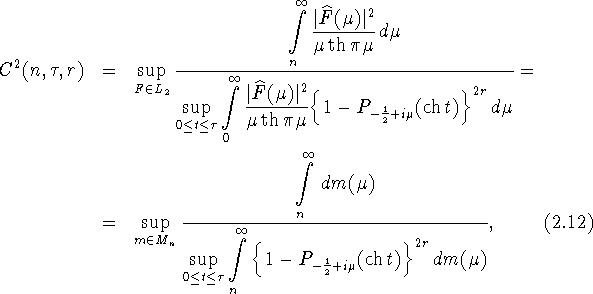
где

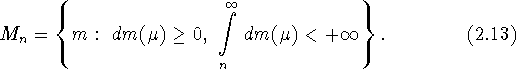
З а м е ч а н и е. Сравнивая формулу (2.13) для величины с формулой (1.6) для величины видим, что они совпадают, т.е.

Таким образом, вычисление величины сводится к вычислению величины которую будем исследовать в следующем параграфе. При исследовании величины C будем использовать методы Н.И.Черныха, В.А.Юдина, А.Г.Бабенко построения экстремального веса для получения оценки сверху константы и схему В.В.Арестова для ее оценки снизу.