Используя общую формулу (16), аналогично (
![]() ), находим
), находим
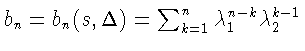 (при
(при
Из (17) следует, что
![]() поэтому
поэтому
![]() если s=0.
если s=0.
Cчитая ![]() введем
введем
![]() тогда
тогда
Найдем циклы уравнения (11) при
![]() (ситуация, когда
(ситуация, когда
![]() описана в п. 2). Точки n-цикла
описана в п. 2). Точки n-цикла
![]() суть
неподвижные точки отображения fn. Обозначим через
суть
неподвижные точки отображения fn. Обозначим через
![]() множество неподвижных точек fn. При
множество неподвижных точек fn. При
![]() при
при
![]() При
При
![]() все множества
все множества
![]() совпадают:
совпадают:
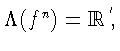 если
если
![]() если
если
![]() Так как
Так как
![]() а fn, как и f -дробно-линейное отображение,
то в случае
а fn, как и f -дробно-линейное отображение,
то в случае
![]() или 1)
или 1)
![]() или 2)
существует наименьшее q>1 такое, что
или 2)
существует наименьшее q>1 такое, что
![]() при k<q,но
при k<q,но
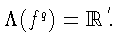 Ситуация 1) наблюдается, в частности,
при
Ситуация 1) наблюдается, в частности,
при
![]() Обозначим символом Kq множество значений
параметра
Обозначим символом Kq множество значений
параметра ![]() отвечающих ситуации 2). Иначе говоря, при
отвечающих ситуации 2). Иначе говоря, при
![]() каркасы решений системы
(1) состоят из q различных O-прямых, за исключением решений
на инвариантных 0-прямых h=h1,2 (такие решения возникают,
когда
каркасы решений системы
(1) состоят из q различных O-прямых, за исключением решений
на инвариантных 0-прямых h=h1,2 (такие решения возникают,
когда
![]() ).
).
Найдем множества Kq. Условие
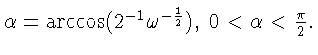 Используя простую формулу
Используя простую формулу
Так как
![]() то n - наименьшее число со
свойством (30) тогда и только тогда, когда (m,n) =1, т.е. m,nвзаимно просты.Поэтому
то n - наименьшее число со
свойством (30) тогда и только тогда, когда (m,n) =1, т.е. m,nвзаимно просты.Поэтому
При
![]() система (1) не
имеет конечных каркасов. В случаях
система (1) не
имеет конечных каркасов. В случаях
Выделим теперь циклы системы (1) при
![]() Каждый цикл лежит
на конечном каркасе, циклы могут существовать лишь при
Каждый цикл лежит
на конечном каркасе, циклы могут существовать лишь при
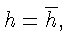 отвечающая такому
собственному значению
отвечающая такому
собственному значению 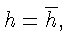 непериодичны.
непериодичны.
В остальных случаях существования циклов (при
![]() )
периодичны
уже все решения системы (1). Соответствующие этим случаям точки
)
периодичны
уже все решения системы (1). Соответствующие этим случаям точки
![]() лежат на множестве
лежат на множестве
![]() тогда
тогда
![]()
Если
![]() то
то
![]() и решения системы - 1-циклы при
и решения системы - 1-циклы при ![]() и 2-циклы,
симметричные относительно O, при
и 2-циклы,
симметричные относительно O, при
![]()
Пусть теперь
![]() Тогда
Тогда
![]() и, значит,
Fq=aqE (см. (23)).
Так как
и, значит,
Fq=aqE (см. (23)).
Так как
![]() то
то
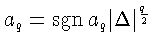 и
и
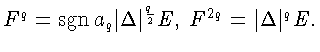 В силу (34)
В силу (34)
![]() Поэтому решения, которые расположены на каркасах, состоящих из q
0-прямых, суть r-циклы, где r=q при aq>0 и r=2q при aq<0.Во втором случае Fq=-E и, значит, 2q-циклы симметричны относительно
Поэтому решения, которые расположены на каркасах, состоящих из q
0-прямых, суть r-циклы, где r=q при aq>0 и r=2q при aq<0.Во втором случае Fq=-E и, значит, 2q-циклы симметричны относительно
![]() Уточним период r циклов в зависимости от
Уточним период r циклов в зависимости от
![]()
Пусть q=2, тогда
![]() и
и
![]() Если
Если
![]() то
то
![]() поэтому r=2 и
решения, не начинающиеся на O-прямой
поэтому r=2 и
решения, не начинающиеся на O-прямой
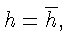 отвечающей
отвечающей
![]() суть 2-циклы; точки 0-прямой - положения равновесия системы.
О таких системах типа "плоскость 2- и 1-циклов" речь уже шла в п. 2. Если
же
суть 2-циклы; точки 0-прямой - положения равновесия системы.
О таких системах типа "плоскость 2- и 1-циклов" речь уже шла в п. 2. Если
же
![]() то
то
![]() и приходим к системе типа
``центр'', решения которой - 4-циклы.
и приходим к системе типа
``центр'', решения которой - 4-циклы.
Пусть теперь ![]() и, значит,
и, значит,
![]() Зафиксируем любое p с указанными свойствами.
Тогда
Зафиксируем любое p с указанными свойствами.
Тогда
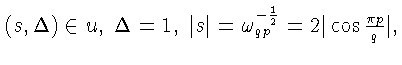 поэтому
рассматриваем cистемы типа ``центр'' с матрицами F из двух семейств
поэтому
рассматриваем cистемы типа ``центр'' с матрицами F из двух семейств
![]() и
и
![]() Для нахождения периода rциклов, учитывая свойство 20, выберем матрицы
Для нахождения периода rциклов, учитывая свойство 20, выберем матрицы
![]() содержащиеся
в каждом семействе. Для матрицы из первого и второго семейств
содержащиеся
в каждом семействе. Для матрицы из первого и второго семейств
![]() и
и
![]() соответственно. Решения системы с матрицей
соответственно. Решения системы с матрицей ![]() за q шагов совершают
поворот вокруг O на угол
за q шагов совершают
поворот вокруг O на угол ![]() в результате чего попадание в исходную точку
происходит лишь при четных p. Поэтому решения системы (1) с матрицей
в результате чего попадание в исходную точку
происходит лишь при четных p. Поэтому решения системы (1) с матрицей
![]() - q-циклы при четных p и 2q-циклы при
нечетных p. Аналогично, в случае
- q-циклы при четных p и 2q-циклы при
нечетных p. Аналогично, в случае
![]() имеем r=q, если
q-p четно, и r=2q, если q-p нечетно.
имеем r=q, если
q-p четно, и r=2q, если q-p нечетно.
Итак, решения системы (1) суть q- или 2q-циклы (![]() ), если
), если
![]() т.е.
т.е.
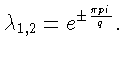 Решения являются q-циклами в случаях
Решения являются q-циклами в случаях
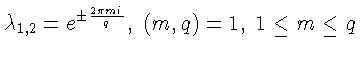 [10, cтр. 103],
т.е. при
[10, cтр. 103],
т.е. при
![]()
Поступила 11.06.97