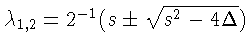 устанавливают биекцию
между парами
устанавливают биекцию
между парами
Парабола
![]() разбивает плоскость P на области
разбивает плоскость P на области
![]()
![]() отвечающие матрицам
отвечающие матрицам ![]() с комплексными и различными
вещественными собственными значениями соответственно. Точкам параболы
отвечают матрицы с кратными собственными значениями.
с комплексными и различными
вещественными собственными значениями соответственно. Точкам параболы
отвечают матрицы с кратными собственными значениями.
Введем еще один параметр
![]() системы, связанный с
системы, связанный с
![]() :
:
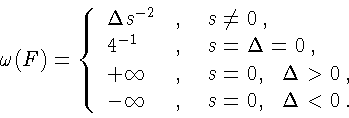
Пусть
![]() тогда 1)
тогда 1)
![]()
![]() 2)
2)
![]() где
где
![]() 3)
3)
![]() при
при
![]() Свойство 1) следует из равенств
Свойство 1) следует из равенств
Изучим структуру множеств
![]()

При
![]()
![]() - семейство подобных матриц.
Если
- семейство подобных матриц.
Если
![]() то
то
![]() и
и
![]() - объединение двух семейств подобных матриц:
одно образовано матрицами, подобными жордановой клетке
- объединение двух семейств подобных матриц:
одно образовано матрицами, подобными жордановой клетке
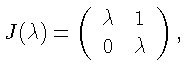 другое содержит лишь скалярную матрицу
другое содержит лишь скалярную матрицу
![]() Из (3) следует, что при
Из (3) следует, что при ![]()
Зафиксировав
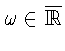 и произвольную матрицу
и произвольную матрицу
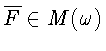 со следом
со следом
![]() и определителем
и определителем
![]() введем множество
введем множество
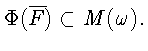 Докажем, что при
Докажем, что при
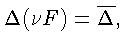 тогда
тогда
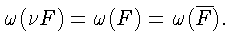 Приходим к равенствам
Приходим к равенствам
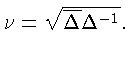 Если же
Если же
Структура семейства M(4-1) сложнее:
![]() здесь
здесь
![]()
![]()
Перейдем к свойствам решений системы (1). Любая из систем имеет тривиальное решение x(n)=0. В дальнейшем, говоря о решениях системы, предполагаем их нетривиальными.
В случаях
![]()
![]() матрица F обладает
собственным базисом e1, e2, образованным из ее собственных векторов,
поэтому все точки каждого решения Fnx,
матрица F обладает
собственным базисом e1, e2, образованным из ее собственных векторов,
поэтому все точки каждого решения Fnx,
![]() раскладываются
по этому базису:
раскладываются
по этому базису:
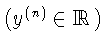 с положением равновесия y=0. Пусть
с положением равновесия y=0. Пусть
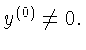 Тогда
Тогда
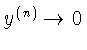 в случае
в случае
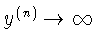 в случае
в случае
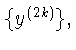
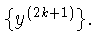 В cлучае
В cлучае
Назовем решение x(n) системы обнуляющимся (на шаге с номером n0),
если
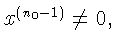 но x(n)=0 при
но x(n)=0 при ![]() Система (1)
имеет обнуляющиеся решения
Система (1)
имеет обнуляющиеся решения
![]() Рассмотрим
этот особый случай подробнее.
Рассмотрим
этот особый случай подробнее.
При ![]() решения системы обнуляются на первом шаге, при
решения системы обнуляются на первом шаге, при
![]() - не позднее чем на втором шаге (это
вытекает из теоремы Кэли-Гамильтона). Здесь
- не позднее чем на втором шаге (это
вытекает из теоремы Кэли-Гамильтона). Здесь ![]() - нулевая матрица.
Как следует из (9), при
- нулевая матрица.
Как следует из (9), при
![]() обнуляются решения, начинающиеся
на O-прямой l1, а остальные решения, начиная с первого шага, лежат на
O-прямой l2 (здесь O-прямая - прямая, проходящая через начало
координат O, lk - O-прямая с направляющим вектором ek).
Поэтому изучение системы (1) при
обнуляются решения, начинающиеся
на O-прямой l1, а остальные решения, начиная с первого шага, лежат на
O-прямой l2 (здесь O-прямая - прямая, проходящая через начало
координат O, lk - O-прямая с направляющим вектором ek).
Поэтому изучение системы (1) при
![]() сводится к рассмотрению
уравнения вида (10). В дальнейшем основное внимание уделено
неособому случаю
сводится к рассмотрению
уравнения вида (10). В дальнейшем основное внимание уделено
неособому случаю
![]()
Так как
![]() то все необнуляющиеся
решения системы (1), начинающиеся на одной O-прямой, гомотетичны
с центром O. Найдем закон изменения O-прямых вдоль таких решений.
Обозначим
то все необнуляющиеся
решения системы (1), начинающиеся на одной O-прямой, гомотетичны
с центром O. Найдем закон изменения O-прямых вдоль таких решений.
Обозначим
 и введем отображение
и введем отображение
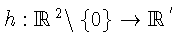
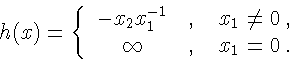
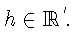
Пусть
![]() Укажем функцию f, задающую изменение координаты hпри переходе от точки
Укажем функцию f, задающую изменение координаты hпри переходе от точки ![]() к точке Fx.
к точке Fx.
Если
![]() то f - дробно-линейный гомеоморфизм множества
то f - дробно-линейный гомеоморфизм множества
![]() на себя:
f(h)=(dh-c)(-bh+a); предполагается, что при
на себя:
f(h)=(dh-c)(-bh+a); предполагается, что при ![]()
![]()
![]() Если b=0, то функция f - линейна:
f(h)=a-1(dh-c),
Если b=0, то функция f - линейна:
f(h)=a-1(dh-c),
![]() и, значит,
и, значит, ![]() - ее
неподвижная точка. Вообще, при
- ее
неподвижная точка. Вообще, при
![]() f имеет две различные
неподвижные точки h1,2, являющиеся координатами O-прямых с направляющими
векторами e1,2. Эти O-прямые инвариантны относительно F(ради краткости матрица F и отображение
f имеет две различные
неподвижные точки h1,2, являющиеся координатами O-прямых с направляющими
векторами e1,2. Эти O-прямые инвариантны относительно F(ради краткости матрица F и отображение ![]() отождествляются). Решения
системы на O-прямых h=h1,2 определяются уравнениями типа (10),где
отождествляются). Решения
системы на O-прямых h=h1,2 определяются уравнениями типа (10),где
![]() y - линейная комбинация фазовых координат.
При
y - линейная комбинация фазовых координат.
При
![]() f - тождественное отображение и все точки
f - тождественное отображение и все точки
 неподвижные точки для f. При
неподвижные точки для f. При
![]() существует
одна неподвижная точка f, а при
существует
одна неподвижная точка f, а при
![]() отображение не имеет
неподвижных точек.
отображение не имеет
неподвижных точек.
Если
![]() то существует одно нулевое собственное значение
то существует одно нулевое собственное значение
![]() матрицы F. Как следует из сказанного выше, функция fпостоянна и не определена в точности в одной точке
матрицы F. Как следует из сказанного выше, функция fпостоянна и не определена в точности в одной точке
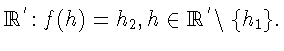
Нами построено отображение G,сопоставляющее матрице
![]() функцию f.
функцию f.
Изменение координаты h вдоль необнуляющихся решений системы (1) описывается разностным уравнением
![]() Если x(n) - решение системы (1), то
Если x(n) - решение системы (1), то
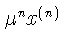 -
решение системы (12).
-
решение системы (12).
В частности, при ![]() точки обоих решений с четными номерами nсовпадают, а точки с нечетными номерами симметричны относительно O.Такому переходу от F к (-F) отвечает, согласно (4), переход
на плоскости P от точки
точки обоих решений с четными номерами nсовпадают, а точки с нечетными номерами симметричны относительно O.Такому переходу от F к (-F) отвечает, согласно (4), переход
на плоскости P от точки
![]() к точке
к точке
![]() Если же
Если же ![]() увеличивается, то, как видно
из
увеличивается, то, как видно
из
![]() система (12) ``ухудшается''. При указанном изменении
система (12) ``ухудшается''. При указанном изменении
![]() точка
точка
![]() движется по линии
движется по линии
![]() от
начала координат (см. (3)). Критерий
от
начала координат (см. (3)). Критерий
![]() асимптотической устойчивости в целом нулевого положения равновесия выделяет
на плоскости P треугольник
асимптотической устойчивости в целом нулевого положения равновесия выделяет
на плоскости P треугольник
![]() ограниченный отрезками
прямых
ограниченный отрезками
прямых
![]()
![]() и отрезком
и отрезком
![]() прямой
прямой ![]() [8, cтр. 111-112] (рис. 1). Здесь
[8, cтр. 111-112] (рис. 1). Здесь
![]() - характеристический многочлен матрицы F.
- характеристический многочлен матрицы F.
Пусть
![]() Укажем типичные бифуркации,
происходящие в системе (12) с ростом
Укажем типичные бифуркации,
происходящие в системе (12) с ростом ![]() При
При
![]() устойчивость
устойчивость ![]() негрубый случай
негрубый случай
![]() неустойчивость (
неустойчивость (
![]() тогда
тогда
![]() при
при
 ). При
). При
![]() :
устойчивость
:
устойчивость ![]() негрубый случай
негрубый случай
![]() система типов ``седло''
система типов ``седло''
![]() негрубый случай
негрубый случай
![]() неустойчивость. При
неустойчивость. При
![]() : устойчивость
: устойчивость ![]() негрубый случай
негрубый случай
![]() неустойчивость. Негрубым случаям
на плоскости P отвечает множество
неустойчивость. Негрубым случаям
на плоскости P отвечает множество
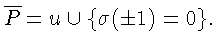 Нетривиальные периодические решения (циклы) в системе (1)
возможны лишь при
Нетривиальные периодические решения (циклы) в системе (1)
возможны лишь при
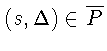 .
.
Если
![]() - неподвижная точка f, то
- неподвижная точка f, то
![]() -каркас
состоит лишь из одной O-прямой
-каркас
состоит лишь из одной O-прямой
![]() В особом случае
В особом случае
![]() и все h-каркасы
и все h-каркасы
![]() состоят не более чем из двух O-прямых:
h(n)=h2 при
состоят не более чем из двух O-прямых:
h(n)=h2 при
![]() Другие случаи систем (1) с конечными каркасами
рассмотрены в п. 3, циклы системы могут находится лишь на конечных каркасах.
Другие случаи систем (1) с конечными каркасами
рассмотрены в п. 3, циклы системы могут находится лишь на конечных каркасах.
В свойствах ![]() и
и ![]() отмечена связь систем (1)
с матрицами из одного класса
отмечена связь систем (1)
с матрицами из одного класса
![]() и из одного семейства
и из одного семейства
![]() (простые случаи
(простые случаи
![]()
![]() здесь опущены).
здесь опущены).
![]() Если F1, F2 - неособые нескалярные матрицы класса
Если F1, F2 - неособые нескалярные матрицы класса
![]() то системы
x(n+1)=F1x(n),
x(n+1)=F2x(n) линейно эквивалентны.
то системы
x(n+1)=F1x(n),
x(n+1)=F2x(n) линейно эквивалентны.
![]() Если F1, F2 - неособые нескалярные матрицы семейства
Если F1, F2 - неособые нескалярные матрицы семейства
![]() то разностные уравнения (11) с функциями
преследования f1=GF1, f2=GF2 топологически эквивалентны.
то разностные уравнения (11) с функциями
преследования f1=GF1, f2=GF2 топологически эквивалентны.
Д о к а з а т е л ь с т в о.
![]() Поскольку
F1, F2 - подобные матрицы, то
F2=T-1F1T. Перейдем в
системе
x(n+1)=F1x(n) к переменной z, полагая x=Tz. Тогда
Tz(n+1)=F1Tz(n) и
z(n+1)=T-1F1Tz(n).
Поскольку
F1, F2 - подобные матрицы, то
F2=T-1F1T. Перейдем в
системе
x(n+1)=F1x(n) к переменной z, полагая x=Tz. Тогда
Tz(n+1)=F1Tz(n) и
z(n+1)=T-1F1Tz(n).
![]() Так как
Так как
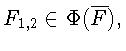 где
где
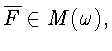 то в силу (5)
то в силу (5)
![]() (
(![]() )
и
)
и
Фазовая плоскость системы (1) переходит в фазовую плоскость линейно ей эквивалентной системы посредством аффинного преобразования с неподвижной точкой O.
При
![]()
![]() собственные значения
матрицы F удобно представлять в тригонометрической форме:
собственные значения
матрицы F удобно представлять в тригонометрической форме:
![]()
![]() В частности, при
В частности, при
![]() и
и
![]() получаем равные собственные значения
получаем равные собственные значения
![]() где
где ![]() и
и
![]()