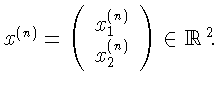Продолжено начатое А. М. Пановым и другими
исследователями изучение системы
где F - постоянная вещественная
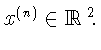 Системе сопоставлено разностное уравнение с
дробно-линейной функцией последования, что позволило установить новые
свойства системы, обнаружить связь систем с различными матрицами F.Системе (1)
при
Системе сопоставлено разностное уравнение с
дробно-линейной функцией последования, что позволило установить новые
свойства системы, обнаружить связь систем с различными матрицами F.Системе (1)
при
такая, что каждое решение системы (1) находится на фазовой траектории (или двух фазовых траекториях) системы (2) Дана полная классификация типов системы (1), указано разбиение плоскости существенных параметров
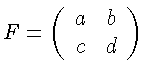 - постоянная матрица,
- постоянная матрица,