Будем говорить, что система (1) является ![]() -дискретизацией
(
-дискретизацией
(![]() )
системы (2), если
)
системы (2), если
![]() Впрочем, выбирая в (2)
вместо A матрицу
Впрочем, выбирая в (2)
вместо A матрицу ![]()
![]() можно добиться, чтобы
можно добиться, чтобы ![]() тогда
тогда
Выясним, когда система (1) является 1-дискретизацией
некоторой системы (2). Условие (14) означает, что A -
вещественный логарифм матрицы F (оказывается матрица F может иметь
бесконечное множество вещественных логарифмов). Известно
[9, cтр. 221],
что необходимым и достаточным условием существования вещественного
![]() является невырожденность матрицы F и отсутствие у нее отрицательных
собственных значений с нечетным числом элементарных делителей.
Свойство (14) справедливо поэтому тогда и только тогда, когда
является невырожденность матрицы F и отсутствие у нее отрицательных
собственных значений с нечетным числом элементарных делителей.
Свойство (14) справедливо поэтому тогда и только тогда, когда
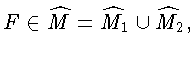 где
где
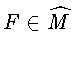 определена функция
Ft,
определена функция
Ft,
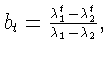
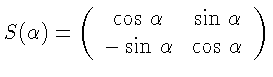 - матрица вращения вокруг O на угол
- матрица вращения вокруг O на угол
Формулы (
![]() ), (
), (
![]() )
сразу следуют из общей формулы
функции от
)
сразу следуют из общей формулы
функции от ![]() -матрицы
-матрицы
Для вывода формулы (
![]() )
предварительно вычисляется
матрица
)
предварительно вычисляется
матрица
![]() (см. (18), k=0), а затем с
учетом (16) находится
(см. (18), k=0), а затем с
учетом (16) находится
![]()
Формулы (15) определяют инвариантные кривые и решения
системы (1) при
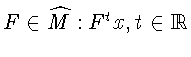 -
инвариантная кривая, проходящая через x,
-
инвариантная кривая, проходящая через x,
![]() -
решение с начальным условием x.
-
решение с начальным условием x.
Используя теорему Кэли-Гамильтона, нетрудно доказать, что функция
![]() удовлетворяет при всяком
удовлетворяет при всяком
![]() линейному разностному уравнению второго порядка
линейному разностному уравнению второго порядка
В случае
![]() формула (
формула (
![]() )
уточняется:
тогда
)
уточняется:
тогда
Однако в случае
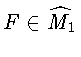 найденное семейство инвариантных кривых
найденное семейство инвариантных кривых
![]() системы (1) не единственно. Действительно, введем функции
системы (1) не единственно. Действительно, введем функции
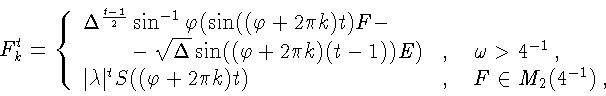
Докажем, что каждая из функций Fkt, если
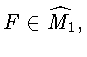 а также
функция Ft, определенная формулой (
а также
функция Ft, определенная формулой (
![]() )
при
)
при
![]() s>0 и формулой (
s>0 и формулой (
![]() )
при
)
при
![]() s>0 является экспоненциалом
s>0 является экспоненциалом
![]() вещественной матрицы
вещественной матрицы
![]() Поэтому выделенные семейства инвариантных
кривых - фазовые траектории соответствующих систем
Поэтому выделенные семейства инвариантных
кривых - фазовые траектории соответствующих систем
![]() откуда и будут следовать при
откуда и будут следовать при
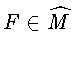 свойства инвариантных
кривых, указанные в начале п. 2.
свойства инвариантных
кривых, указанные в начале п. 2.
Убедимся, что матрица
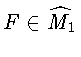 имеет счетное множество
lnkF,
имеет счетное множество
lnkF,
![]() вещественных значений логарифма, тогда
elnkFt=Fkt. Зададимся вначале матрицей
вещественных значений логарифма, тогда
elnkFt=Fkt. Зададимся вначале матрицей
![]()
![]() Укажем
Укажем
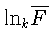 для матрицы
для матрицы
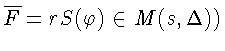 :
:
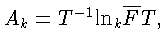 тогда
тогда
В случае
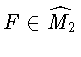 рассуждения такие же, как и при
рассуждения такие же, как и при
![]() :
если
:
если
![]() s>0, то выбираем
s>0, то выбираем
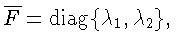 тогда
тогда
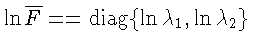 ;
если же
;
если же
![]() s>0, то
s>0, то
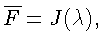
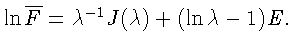 Матрица
Матрица
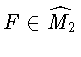 имеет лишь один
вещественный логарифм.
имеет лишь один
вещественный логарифм.
Рассмотрим подробнее ситуацию
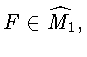 когда система (1)
является
1-дискретизацией счетного множества систем
когда система (1)
является
1-дискретизацией счетного множества систем
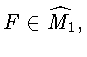
Зафиксировав
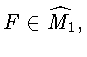
![]() уточним, как отличаются
различные инвариантные кривые Fktx системы (1). Переходя из
положения Fnx в положение Fn+1x, кривые Fktx, k>0,в отличие от F0tx, дополнительно совершают k оборотов вокруг O.Случай k<0 различается тем, что попадание из Fnx в Fn+1xтеперь происходит во вращении в противоположном направлении, но
последний из k оборотов неполный. Поэтому во многих случаях более
простым представляется семейство
уточним, как отличаются
различные инвариантные кривые Fktx системы (1). Переходя из
положения Fnx в положение Fn+1x, кривые Fktx, k>0,в отличие от F0tx, дополнительно совершают k оборотов вокруг O.Случай k<0 различается тем, что попадание из Fnx в Fn+1xтеперь происходит во вращении в противоположном направлении, но
последний из k оборотов неполный. Поэтому во многих случаях более
простым представляется семейство
![]() Тип системы (1)
при
Тип системы (1)
при
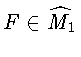 в таблице совпадает с типом системы
в таблице совпадает с типом системы
![]() Полезно, однако, иметь в виду условность выбора конкретного семейства
Полезно, однако, иметь в виду условность выбора конкретного семейства
![]() ;
так, при F=-E (тогда
;
так, при F=-E (тогда
![]() )
фрагменты F0tx,
F-1tx,
)
фрагменты F0tx,
F-1tx,
![]()
![]() инвариантных кривых - дуги полуокружностей с центром O, пробегаемые
в противоположных направлениях.
инвариантных кривых - дуги полуокружностей с центром O, пробегаемые
в противоположных направлениях.
В случае
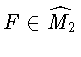 система (1) - дискретизация единственной
системы
система (1) - дискретизация единственной
системы
![]() тип которой будем считать типом исходной системы.
Здесь возникают типы ``узел'' (устойчивый и неустойчивый), ``седло'' и
различные негрубые случаи. Среди последних выделим типы ``аттракторы'',
``репеллеры'', ``сдвиги''. Эти термины введены здесь для обозначения
ситуаций в системах (1) с особой матрицей
тип которой будем считать типом исходной системы.
Здесь возникают типы ``узел'' (устойчивый и неустойчивый), ``седло'' и
различные негрубые случаи. Среди последних выделим типы ``аттракторы'',
``репеллеры'', ``сдвиги''. Эти термины введены здесь для обозначения
ситуаций в системах (1) с особой матрицей
![]() Тогда существует
Тогда существует
![]() при этом соответственно
при этом соответственно
![]() ;
;
![]() ;
;
![]()
![]() На фазовой плоскости наблюдаем O-прямую h=hiположений равновесия системы. В первых двух случаях инвариантные кривые,
отличные от положений равновесия - лучи на прямых, параллельных
O-прямой h=hj, отсекаемые прямой h=hi. Движение
вдоль каждого луча происходит по направлению к соответствующему положению
равновесия (тип ``аттракторы'') и от него (тип ``репеллеры''). В случае
системы типа ``сдвиги'' инвариантные кривые являются прямыми, параллельными
прямой h=hi, а движение вдоль них равномерно.
На фазовой плоскости наблюдаем O-прямую h=hiположений равновесия системы. В первых двух случаях инвариантные кривые,
отличные от положений равновесия - лучи на прямых, параллельных
O-прямой h=hj, отсекаемые прямой h=hi. Движение
вдоль каждого луча происходит по направлению к соответствующему положению
равновесия (тип ``аттракторы'') и от него (тип ``репеллеры''). В случае
системы типа ``сдвиги'' инвариантные кривые являются прямыми, параллельными
прямой h=hi, а движение вдоль них равномерно.
Пусть теперь
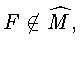
![]() Тогда существует
Тогда существует
![]() Введем матрицу B=F2. Для нее
Введем матрицу B=F2. Для нее
![]()
![]()
![]() Точнее,
Точнее,
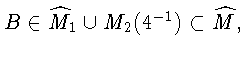 причем
причем
![]() лишь в случае s(F)=0,
лишь в случае s(F)=0,
![]() Значит, для системы
Значит, для системы
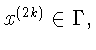
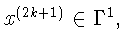
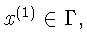 то
то
| Тип системы | Условия на s, |
Условия на
|
|
| 1 | Устойчивый фокус |
|
|
| 2 | Неустойчивый фокус |
|
|
| 3 | Устойчивый узел |
|
|
| 0<s<2 | |||
| 4 | Устойчивый |
|
|
| узел-2 | -2<s<0 | ||
| 5 | Устойчивый |
|
|
| узел-3 |
|
||
| 6 | Неустойчивый узел |
|
|
| s>2 | |||
| 7 | Неустойчивый |
|
|
| узел-2 | s<-2 | ||
| 8 | Неустойчивый |
|
|
| узел-3 |
|
||
| 9 | Седло |
|
|
|
|
|||
| 10 | Седло-2 |
|
|
|
|
|||
| 11 | Седло-3 |
|
|
|
|
|||
| 12 | Центр |
|
|
| 13 | Устойчивый дикритический узел. Устойчивый вырожденный узел |
|
|
| 14 | Неустойчивый дикритический узел. Неустойчивый вырожденный узел |
|
|
| 15 | Устойчивый фокус. Устойчивый вырожденный узел-2 |
|
|
|
Если
![]() то кривые
то кривые ![]()
![]() симметричны
относительно O. Если же
симметричны
относительно O. Если же
![]() и
и
![]() (
(
![]() ), то эти кривые расположены по разные стороны от O-прямой
h=h2 (h=h1); в случае диагональной матрицы F они относительно
O-прямой симметричны.
), то эти кривые расположены по разные стороны от O-прямой
h=h2 (h=h1); в случае диагональной матрицы F они относительно
O-прямой симметричны.
Тип системы (1) определяется теперь типом системы (21) и
![]() Обозначив условно тип системы (21) символом
``Т'', при
Обозначив условно тип системы (21) символом
``Т'', при
![]() будем говорить о системе (1) типа
``Т-2'', а при
будем говорить о системе (1) типа
``Т-2'', а при
![]() - о системе (1) типа
``Т-3''. Впрочем, в случае
- о системе (1) типа
``Т-3''. Впрочем, в случае
![]() отвечающем вершине
отвечающем вершине
![]() треугольника устойчивости V, отойдем от названного
принципа классификации: тогда
треугольника устойчивости V, отойдем от названного
принципа классификации: тогда
![]() и для любого
решения системы (1)
и для любого
решения системы (1) ![]()
![]() -точки. Как видно
из (9), решения системы периодичны, являясь 2-циклами при
-точки. Как видно
из (9), решения системы периодичны, являясь 2-циклами при
![]() и 1-циклами при c2=0; в этом случае представляется
естественным термин ``плоскость 2- и 1-циклов''.
и 1-циклами при c2=0; в этом случае представляется
естественным термин ``плоскость 2- и 1-циклов''.
Пусть
![]() и
и
![]()
![]() Как
отмечено в п. 1, все необнуляющиеся решения системы (1), начиная с
первого шага, находятся на O-прямой h=h2, которую можно считать
единственной инвариантной кривой. Поведение решений на O-прямой описывается
уравнением вида (10), где
Как
отмечено в п. 1, все необнуляющиеся решения системы (1), начиная с
первого шага, находятся на O-прямой h=h2, которую можно считать
единственной инвариантной кривой. Поведение решений на O-прямой описывается
уравнением вида (10), где
![]() При
При
![]() в зависимости от
в зависимости от
![]()
![]() возникают системы (1) типов
``сингулярный узел'', ``сингулярный узел-2'' (устойчивые и неустойчивые)
[1]. В случае
возникают системы (1) типов
``сингулярный узел'', ``сингулярный узел-2'' (устойчивые и неустойчивые)
[1]. В случае
![]() наблюдаем ``прямую положений
равновесия'', а в случае
наблюдаем ``прямую положений
равновесия'', а в случае
![]() ``прямую 2-циклов''. Если, наконец,
``прямую 2-циклов''. Если, наконец,
![]() то Fkx=0, k=1 или k=2, и будем говорить об
``обнулении''.
то Fkx=0, k=1 или k=2, и будем говорить об
``обнулении''.
Классификация типов системы (1) дана в таблице, в ней же и на
рис. 1 см. разбиение плоскости P на множества, отвечающие системам каждого
типа ( P-множества типов). Для случаев, где
![]() в таблице
приведено название двух типов: первым указан тип системы при
в таблице
приведено название двух типов: первым указан тип системы при
![]() вторым - при
вторым - при
![]()
Плоскость P разбивается на 11 P-множеств грубых типов и на 21
P-множество негрубых типов. P-множества грубых типов - открытые
множества, отделенные линиями, содержащимися во множестве бифуркаций
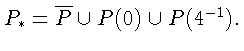 P-множества негрубых типов
- дуги линий или отдельные точки, лежащие на P*. При этом
P-множество типа ``Т-2'' симметрично P-множеству типа ``Т'' относительно
оси ординат. В свою очередь, P-множество типа ``Т-3'' симметрично
относительно этой оси.
P-множества негрубых типов
- дуги линий или отдельные точки, лежащие на P*. При этом
P-множество типа ``Т-2'' симметрично P-множеству типа ``Т'' относительно
оси ординат. В свою очередь, P-множество типа ``Т-3'' симметрично
относительно этой оси.