чной мерой существует центрально-симметричное антипроксиминальное множество
Теорема 1.В бесконечномерном
пространстве
![]() с
с ![]() коне-
коне-
чной мерой существует
центрально-симметричное антипроксиминальное множество
![]() такое, что
такое, что
![]() ограниченно.
ограниченно.
Д о к а з а т е л ь с т в о получаем из леммы 6 и предложения 1.
Лемма 7.Пусть X - банахово
пространство,
![]() - выпуклое антипроксиминальное в Xтело,
- выпуклое антипроксиминальное в Xтело,
![]() тогда
тогда
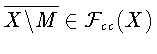 антипроксиминально,
а
антипроксиминально,
а
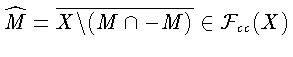 -
центрально-симмет-
-
центрально-симмет-
ричное антипроксиминальное в X множество.
Д о к а з а т е л ь с т в о. Имеем
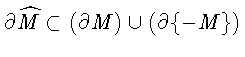 .
Если
найдутся
.
Если
найдутся
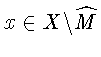 и
и
![]() то можем считать, без потери общности, что
то можем считать, без потери общности, что
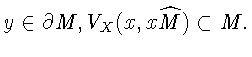 По теореме Хана-Банаха найдется линейный непрерывный функционал
По теореме Хана-Банаха найдется линейный непрерывный функционал
![]() Имеем
Имеем
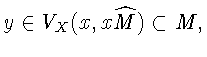 следовательно,
следовательно,
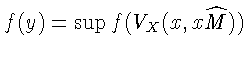 и для
и для
![]() справедливо включение
справедливо включение
![]() Тогда для
Тогда для
![]() справедливо
справедливо
![]() Но,
Но,
![]() следовательно,
следовательно,
![]() противоречие,
противоречие,
![]() и
и
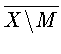 антипроксиминальны.
антипроксиминальны.
Теорема 2.В пространстве C(Q) , где Q - бесконечный бикомпакт, существует центрально-симметричное
антипроксиминальное множество
![]() такое, что
такое, что
![]() ограниченно.
ограниченно.
Д о к а з а т е л ь с т в о получаем из леммы 7 и результата [4]: в пространстве C(Q), где Q - бесконечный бикомпакт, существует непустое выпуклое замкнутое ограниченное антипроксиминальное множество.
З а м е ч а н и е . Утверждение обратное к утверждению леммы 7
неверно. По теореме 1 во всех бесконечномерных пространствах
![]() (
(
![]() -конечна) существуют
антипроксиминальные множества
-конечна) существуют
антипроксиминальные множества
![]() такие, что
такие, что
![]() ограниченно, но если
ограниченно, но если ![]() имеет атом положительной конечной меры, то
ограниченных замкнутых выпуклых антипроксиминальных
множеств нет [14], в частности в l1. Их нет [15] и в банаховых пространствах со
свойством Радона-Никодима, в том числе в рефлексивных.
Следствие 3 показывает, что в
рефлексивных банаховых пространствах нет также антипроксиминальных множеств
с выпуклым дополнением.
имеет атом положительной конечной меры, то
ограниченных замкнутых выпуклых антипроксиминальных
множеств нет [14], в частности в l1. Их нет [15] и в банаховых пространствах со
свойством Радона-Никодима, в том числе в рефлексивных.
Следствие 3 показывает, что в
рефлексивных банаховых пространствах нет также антипроксиминальных множеств
с выпуклым дополнением.
Лемма 8[18].Пусть
![]() Если из
Если из
![]() вытекает
вытекает
![]() то или
то или
![]() или
или
![]()
Лемма 9.Пусть
![]() Если для любых последовательностей xn, fn таких, что
Если для любых последовательностей xn, fn таких, что
![]() имеем
имеем
![]() то функция расстояния
то функция расстояния ![]() дифференцируема по Фреше в точке x.
дифференцируема по Фреше в точке x.
Д о к а з а т е л ь с т в о. Обозначим
![]()
Докажем, что
![]() .
Допустим противное:
.
Допустим противное:
![]() .
Пусть
.
Пусть
![]() Возьмем
Возьмем
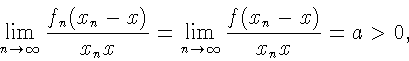
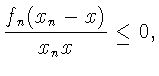 так как
так как
Возьмем произвольную последовательность
![]()
Рассмотрим случай, когда
![]() Имеем
Имеем
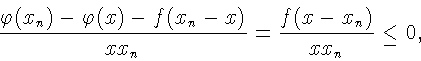
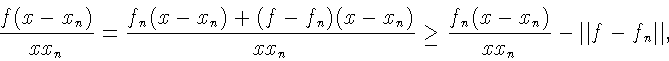
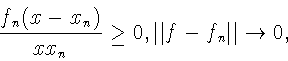
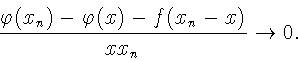
Рассмотрим случай, когда
![]() Возьмем
последовательность
Возьмем
последовательность
![]() такую, что
такую, что
![]() тогда
тогда
![]() Пусть
Пусть
![]() .
По условию
.
По условию
![]() Как доказано выше,
Как доказано выше,
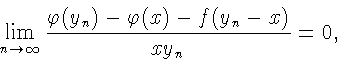
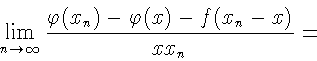
![\begin{displaymath}=
\lim\limits_{n\to\infty}\left[\frac{\varphi(y_n ) - \varph...
...{\varphi(x_n ) -
\varphi(y_n ) - f(x_n - y_n) }{xx_n}\right] =
\end{displaymath}](img403.gif)
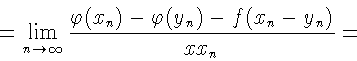
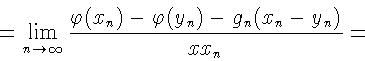
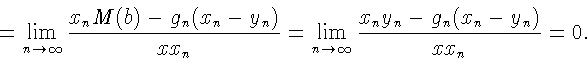
Остался случай, когда
![]() Пусть
Пусть
![]() Имеем
Имеем
![]() по условию
по условию
![]() Имеем
Имеем
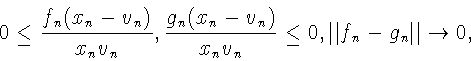
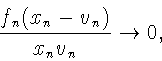
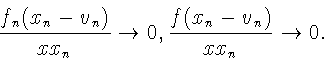
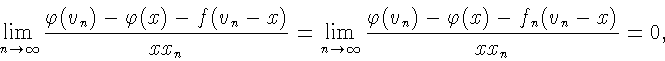
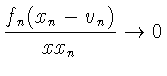 получаем
получаем
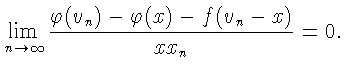
Лемма 10.Пусть
![]()
![]() Тогда
Тогда
![]()
Д о к а з а т е л ь с т в о. Пусть
![]() .
.
Рассмотрим случай, когда
rn > a > 0 для всех номеров
n. Возьмем последовательность
![]() и
и ![]() такие, что
такие, что
![]() Возьмем точку
Возьмем точку
![]() такую, что
такую, что
![]() и
и
![]() Имеем по условию
Имеем по условию
![]() следовательно,
следовательно,
![]() Имеем
Имеем
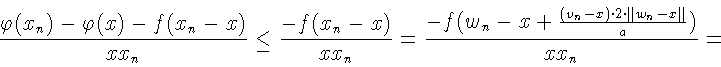
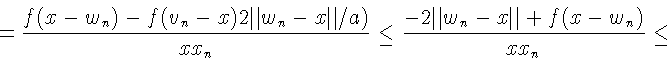
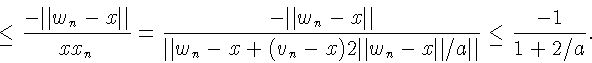
Следствие 6.Пусть
![]() Следующие условия эквивалентны:
Следующие условия эквивалентны:
а)в точке x функция расстояния ![]() дифференцируема
по Фреше;
дифференцируема
по Фреше;
б)для
![]() имеем
имеем
![]()
в)если для
![]() справедливо равенство
справедливо равенство
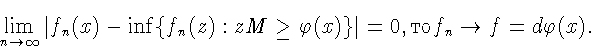
Д о к а з а т е л ь с т в о. а)
![]() в) по
лемме 10, в)
в) по
лемме 10, в)
![]() б) очевидно,
б) очевидно,
б)
![]() а) по лемме 9.
а) по лемме 9.
Нам потребуются следующие обозначения:
GM - множество тех ![]() где
где ![]() имеет
производную
Гато
имеет
производную
Гато
![]() так что
так что
![]()
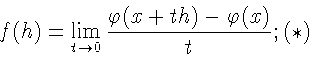
FM - множество тех ![]() где предел (*) равномерен по
где предел (*) равномерен по
![]() (в этом случае f называется производной Фреше, а
(в этом случае f называется производной Фреше, а ![]() дифференцируемой по Фреше в точке x);
дифференцируемой по Фреше в точке x);
![]()
Теорема 3.Пусть
![]() Тогда:
Тогда:
а)
![]() достигает максимума на N только в одной точке;
достигает максимума на N только в одной точке;
б)
![]() достигает максимума на N только в одной точке и
эта точка принадлежит
достигает максимума на N только в одной точке и
эта точка принадлежит
![]()
в)
![]() -
сильно* достигающий функционал
для N.
-
сильно* достигающий функционал
для N.
Д о к а з а т е л ь с т в о. а).
Доказательство импликации "
![]() ". По известной
теореме, см., например, [21, стр. 29] ,
существует единственный
функционал
". По известной
теореме, см., например, [21, стр. 29] ,
существует единственный
функционал
![]() такой, что
такой, что
![]() Так как
Так как
![]() то
то
![]()
Доказательство импликации "
![]() ". Пусть
". Пусть
![]() достигает максимума на N только в одной точке, обозначим
ее через
f. Как известно, для дифференцируемости по Гато
непрерывной вогнутой функции
достигает максимума на N только в одной точке, обозначим
ее через
f. Как известно, для дифференцируемости по Гато
непрерывной вогнутой функции ![]() в точке x необходимо и достаточно, чтобы в точке
в точке x необходимо и достаточно, чтобы в точке
![]() существовала единственная опорная к подграфику
гиперплоскость. Допустим, что в точке
существовала единственная опорная к подграфику
гиперплоскость. Допустим, что в точке
![]() к C касательны
две различные гиперплоскости, т.е. существуют
к C касательны
две различные гиперплоскости, т.е. существуют
![]() такие, что
такие, что
![]()
![$[\overline{\mathbf{x}} - K]\cap
Y_{+} \subset
\widetilde{C} = C,$](img468.gif) то
то
б). Доказательство импликации "
![]() ". Имеем
". Имеем
![]() по доказанному в пункте а)
по доказанному в пункте а)
![]() достигает
максимума в некоторой единственной точке
достигает
максимума в некоторой единственной точке
![]() По лемме 3(д)
По лемме 3(д)
![]() достигает максимума на Cв точке
достигает максимума на Cв точке
![]() Поскольку
Поскольку
![]() то найдется
то найдется
![]() такое, что для любого числа
такое, что для любого числа
![]() найдутся
найдутся
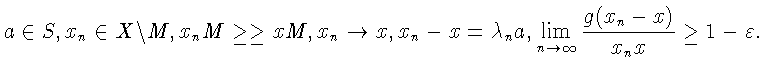 В силу
В силу
![]() имеем
имеем
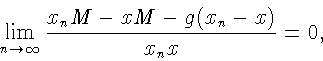
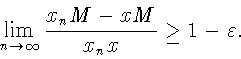
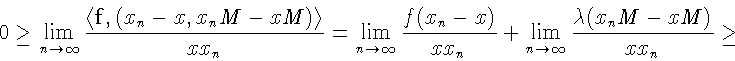
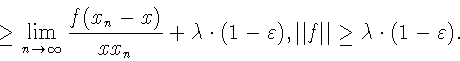
Доказательство импликации "
![]() ". По пункту (а)
". По пункту (а)
![]() Осталось доказать, что
Осталось доказать, что
![]() Пусть
Пусть
![]() достигает максимума в точке
достигает максимума в точке
![]() Имеем
Имеем
![]() По лемме 3(а) и 3(д)
По лемме 3(а) и 3(д)
![]() Пусть
Пусть
![]() имеем
имеем
![]() следовательно
следовательно
![]() где
где
![]() Так как
Так как
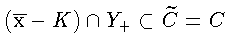 , то по лемме 1(б)
гиперплоскость
, то по лемме 1(б)
гиперплоскость
![]() касательна к
касательна к
![]() и xM = xH. Ясно, что
и xM = xH. Ясно, что
![]() .
Возьмем
.
Возьмем ![]() такую, что
такую, что
![]() Пусть
Пусть
![]() Считаем, без потери общности, что
Считаем, без потери общности, что
![]() Имеем
Имеем
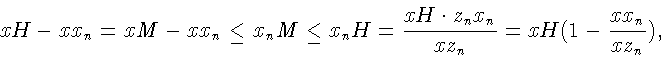
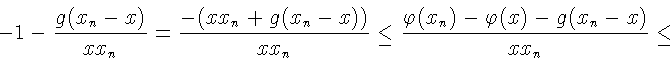
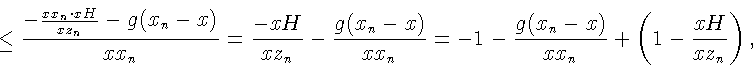
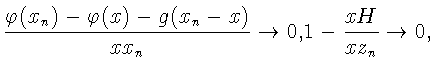 следовательно,
следовательно,
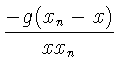
в). Доказательство импликации "
![]() ". Пусть
". Пусть
![]() По пункту (б) существует единственный
функционал
По пункту (б) существует единственный
функционал
![]() такой, что
такой, что
![]() и
и
![]() Если
Если
![]() не является сильно* достигающим функционалом, то
найдутся
не является сильно* достигающим функционалом, то
найдутся
![]() и число
и число
![]() такие, что
такие, что
![]()
Рассмотрим множества
![]()
![]() следовательно,
следовательно,
![]() тогда
тогда
![]() -
cl co An.Если бы было
-
cl co An.Если бы было
![]() то
то
![]() -
-
![]() что невозможно. Поэтому
что невозможно. Поэтому
![]() Обозначим
Обозначим
![]() .
По лемме 1[3] Q выпукло. Имеем
.
По лемме 1[3] Q выпукло. Имеем
![]()
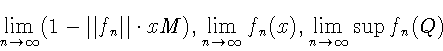
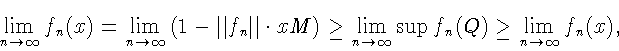
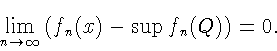
Доказательство импликации "
![]() ". Пусть теперь
". Пусть теперь
![]() -
сильно* достигающий функционал для
-
сильно* достигающий функционал для
![]() по лемме 3 (д)
по лемме 3 (д)
![]() По лемме 3(г)
По лемме 3(г)
![]() .
Пусть
.
Пусть
![]() тогда
тогда
![]() Возьмем любые
Возьмем любые
![]() такие, что
такие, что
![]() тогда по лемме 3(д)
тогда по лемме 3(д)
![]() Так как
Так как
![]() то последовательность
то последовательность
![]() ограниченна. Имеем
ограниченна. Имеем
Следствие 7 [3].Пусть
![]() Тогда
Тогда
![]()
Следствие 8 [3].Пусть
![]() Тогда
Тогда
![]()
Д о к а з а т е л ь с т в а следствий 7 и 8 получаются из
леммы 5 и теоремы 3(б).
Л.П.Власов [8] доказал следующие утверждения:
Пусть X - банахово пространство, X* строго выпукло,
![]() Если (а)
Если (а)
![]() или (б)
или (б)
![]() то M выпукло.
то M выпукло.
Следующая теорема обобщает и уточняет эти утверждения.