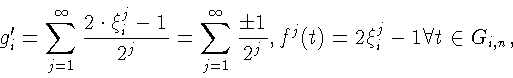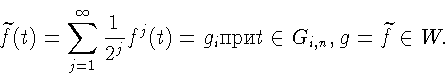Подмножество
![]() линейного нормированного пространства X называется
антипроксиминальным, если для любой точки
линейного нормированного пространства X называется
антипроксиминальным, если для любой точки
![]() в множестве A нет ближайшей точки.
в множестве A нет ближайшей точки.
Известно [2], что в пространстве
l1 с некоторой новой эквивалентной нормой
можно построить антипроксиминальное множество с ограниченным
выпуклым дополнением.
В настоящей работе такие множества будут
построены в бесконечномерных пространствах
![]()
![]() О выпуклых антипроксиминальных
множествах см. в [4], где имеются ссылки на других
авторов.
О выпуклых антипроксиминальных
множествах см. в [4], где имеются ссылки на других
авторов.
О б о з н а ч е н и я.
X - линейное нормированное пространство,
![]() - числовая прямая,
- числовая прямая,
![]() 2
2
![]() для
для
![]() полагаем
f(x) =
полагаем
f(x) =
![]()
![]()
![]()
![]()
![]()
![]() достигает
максимума на
достигает
максимума на
![]() достигает максимума
на
достигает максимума
на
![]() .
Всюду в работе элементы
.
Всюду в работе элементы
![]() и
и
![]() будем отождествлять с x и fсоответственно;
для
будем отождествлять с x и fсоответственно;
для
![]() будем сокращать
будем сокращать
![]() до
до
![]() до
до
![]() до
до
![]() Всюду в работе
Всюду в работе
![]() Будем обозначать через
(B), (R), (Rf) класс банаховых, строго выпуклых,
рефлексивных пространств соответственно.
Будем обозначать через
(B), (R), (Rf) класс банаховых, строго выпуклых,
рефлексивных пространств соответственно.
Пусть
![]() через
intM обозначим множество
внутренних точек множества M, через
через
intM обозначим множество
внутренних точек множества M, через
![]() - замыкание множества
- замыкание множества
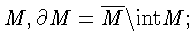 через
conv M - выпуклую оболочку множества
через
conv M - выпуклую оболочку множества
![]() - функция расстояния
от x до
- функция расстояния
от x до
![]() - ее производная (по Гато или Фреше) ;
- ее производная (по Гато или Фреше) ;
![]()
![]() не более чем одноточечно
не более чем одноточечно
![]()
![]()
![]()
![]()
![]()
Для подпространства
![]() через
через ![]() будем обозначать
аннулятор
будем обозначать
аннулятор
![]()
Через
![]() обозначим поляры множеств
обозначим поляры множеств
![]() соответственно;
соответственно;
![]() называется
биполярой M, N, соответственно. Поляры относительно
X, X* не используются.
называется
биполярой M, N, соответственно. Поляры относительно
X, X* не используются.
Пусть
![]() обозначим через
w*-
обозначим через
w*-
![]() w*-замыкание выпуклой оболочки множества
N в пространстве Y*.
w*-замыкание выпуклой оболочки множества
N в пространстве Y*.
![]() - класс замкнутых непустых множеств из X,
- класс замкнутых непустых множеств из X,
![]() - класс замкнутых непустых множеств из X с выпуклым
дополнением.
- класс замкнутых непустых множеств из X с выпуклым
дополнением.
![]() - класс замкнутых непустых выпуклых ограниченных
множеств
- класс замкнутых непустых выпуклых ограниченных
множеств
![]() таких, что
таких, что
Лемма 1.Пусть X - линейное нормированное пространство. Справедливы следующие соотношения:
а)
![]() ;
;
б)для
![]() такого,
что
такого,
что
![]() имеет место равенство
имеет место равенство
![]() ;
;
в)для
![]() имеет место равенство
имеет место равенство
![]() ;
;
г)
![]()
д)
![]()
Д о к а з а т е л ь с т в о. а). Пусть
![]() Докажем, что
Докажем, что
![]() Пусть
Пусть
![]() но
но
![]() и
и
![]() Рассмотрим
Рассмотрим
![]() где
где
![]() По определению
По определению
![]() Имеем
Имеем
б) и в) доказываются непосредственной проверкой.
г). По пункту а)
![]() для любого
для любого
![]() Пусть
Пусть
![]() и
и
![]() т.е.
т.е.
![]() Возьмем произвольный функционал
Возьмем произвольный функционал
![]() - произвольная точка,
- произвольная точка,
![]() Имеем
Имеем
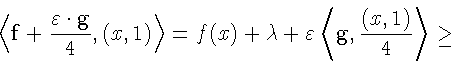
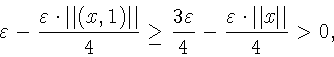
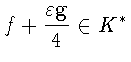 и
и
д). Равенство
![]() получается из пунктов а)
получается из пунктов а)
и г).
О п р е д е л е н и е. Пусть
![]() Точка
Точка
![]() называется сильно* достижимой
называется сильно* достижимой
![]() -
exp*
N), если существует такое
-
exp*
N), если существует такое
![]() что
что
![]() и из условий
и из условий
![]() следует, что
следует, что
![]() функционал
xбудем называть сильно* достигающим.
функционал
xбудем называть сильно* достигающим.
Для
![]() применяются следующие обозначения:
применяются следующие обозначения:
Нам понадобится следующий аналог полярного соответствия между множествами в X и в Y*:
![]() множеству
множеству
![]() ставится в соответствие множество
ставится в соответствие множество
![]() (в лемме 3 будет показано,
что
(в лемме 3 будет показано,
что
![]() ).
).
![]() множеству
множеству
![]() ставится в соответствие
множество
ставится в соответствие
множество
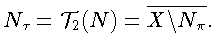
В лемме 4 будет показано, что
![]() по аналогии с теоремой о биполяре.
по аналогии с теоремой о биполяре.
Лемма 2.Пусть X - линейное нормированное
пространство,
![]() -
-
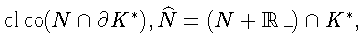 тогда
тогда

Д о к а з а т е л ь с т в о. Включение
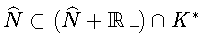 очевидно. С другой стороны,
очевидно. С другой стороны,
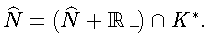
Докажем, что
![]() -
-
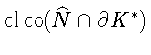 .
Включение
.
Включение
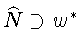 -
-
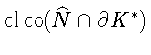 очевидно.
С другой стороны, обозначим W = w*-
очевидно.
С другой стороны, обозначим W = w*-
![]() Ясно, что
Ясно, что
![]() -
-
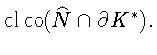 Если теперь
Если теперь
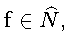 то найдется
то найдется
![]() такое, что
такое, что
![]() где
где
![]() Поэтому
Поэтому
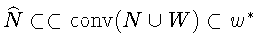 -
-
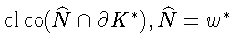 -
-
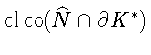 и
и

Лемма 3.Пусть X - линейное нормированное
пространство,
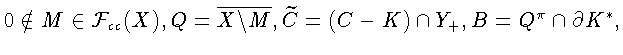
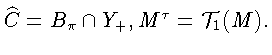
Тогда :
а)
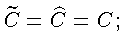
б)
![]()
в)для любого
![]()
г)n-
![]()
д)
если
![]() и
и
![]() то
то
![]()
![]() и
и
![]() при
при
![]()
Д о к а з а т е л ь с т в о. а). Включение
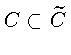 очевидно.
Докажем,
что
очевидно.
Докажем,
что
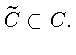 Возьмем произвольную точку
Возьмем произвольную точку
![]() и любую точку
и любую точку
![]() Пусть
Пусть
![]() Имеем
Имеем
![]() так как
так как
![]() Кроме того,
Кроме того,
![]() ,
по определению
множества C, следовательно,
,
по определению
множества C, следовательно,
![]() и
и
![]() По лемме 1 [3] функция
По лемме 1 [3] функция
![]() вогнута на множестве Q, следовательно, C выпукло, тогда
вогнута на множестве Q, следовательно, C выпукло, тогда
![$
(z,\gamma)
\in [\widehat {z},\mathbf{x}]\subset
\linebreak
\subset C, C = \widetilde C.
$](img150.gif)
Пусть
![]() тогда в силу
тогда в силу
![]() имеем
имеем
![]() Если
Если
![]() то
то
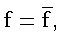
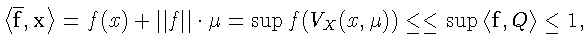 следовательно,
следовательно,
![]() и
и
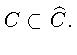
Пусть
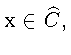 но
но
![]() т.е. выполняется одно из двух условий:
т.е. выполняется одно из двух условий:
![]() или
или ![]() Тогда найдутся точка
Тогда найдутся точка
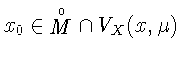 (при выполнении
условия
(при выполнении
условия
![]() возьмем
x0 = x) и
функционал
возьмем
x0 = x) и
функционал
![]() такой, что
такой, что
![]() тогда
тогда
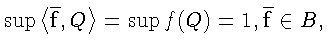 но
но
![]() что противоречит условию
что противоречит условию
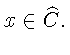 Итак,
Итак,
![]()
б). Множество ![]() выпукло, так как является пересечением
выпуклого конуса и поляры, w*-замкнуто как пересечение
двух w*-замкнутых множеств.
выпукло, так как является пересечением
выпуклого конуса и поляры, w*-замкнуто как пересечение
двух w*-замкнутых множеств.
![]() ,
так как
,
так как
![]()
Ограниченность ![]() следует из того, что
следует из того, что
![]() тогда в силу w*-замкнутости
тогда в силу w*-замкнутости
![]() -бикомпактно.
-бикомпактно.
Равенство
![]() следует из того, что для любого
следует из того, что для любого
![]() и любого
и любого
![]() выполняется
выполняется
![]() (т.е.
(т.е.
![]()
Докажем, что
![]() -
-
![]() .
Включение
.
Включение
![]() -
-
![]() очевидно.
С другой стороны, обозначим A = w*-
очевидно.
С другой стороны, обозначим A = w*-
![]() Имеем
Имеем
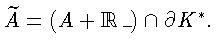 Ясно, что
Ясно, что
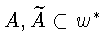 -
-
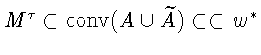 -
-
Докажем, что
![]() Так как
Так как
 имеем
имеем
в). По пункту б) имеем
![]() тогда
по определению класса
тогда
по определению класса ![]()
имеем
![]() следовательно,
следовательно,
г). По пункту в) имеем
д). Так как
![]() то
найдется
то
найдется
![]() такое, что
такое, что
![]()
![]() Тогда
Тогда
![]() Поскольку
Поскольку
![]() то
то
![]() следовательно,
следовательно,
![]() а так как
а так как
![]() то
то
![]() Если бы для
Если бы для
![]() было
было
![]() то
то
Лемма 4.Пусть X - линейное нормированное
пространство,
![]() .
Тогда
.
Тогда
а)
![]()
б)
![]() .
.
Д о к а з а т е л ь с т в о. а). Имеем по лемме 3
![${\cal T}_{1}(M) =
\linebreak
= (C - K)^{\pi}, {\cal T}_{2}({\cal T}_{1}(M)) =
\...
...\overline{C - K}\cap Y_{+}\right]} =
\linebreak
= \overline{X\backslash C} = M.$](img224.gif)
б). Так как N ограниченно, то
![]() замкнутое
выпуклое тело в пространстве
замкнутое
выпуклое тело в пространстве
![]() . Обозначим
. Обозначим
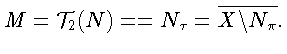
По множеству M определим, как в лемме 3, множества
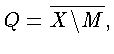
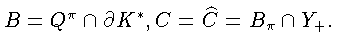 Тогда
Тогда
О п р е д е л е н и е. Банахово пространство X удовлетворяет условию
![]() если каждая достижимая точка единичного
шара пространства X является точкой гладкости.
если каждая достижимая точка единичного
шара пространства X является точкой гладкости.
З а м е ч а н и е. Условие (BB) ранее рассматривали В.И. Бердышев
[9] и А.Брондстед [10] в связи с проблемой
выпуклости чебышевских
множеств в конечномерных пространствах.
Через
expVX(0,1) будем обозначать множество достижимых
точек шара
VX(0,1).
Лемма 5.Пусть X - линейное нормированное пространство,
![]()
Тогда:
а)для того , чтобы ![]() необходимо и достаточно,
чтобы существовал функционал
необходимо и достаточно,
чтобы существовал функционал
![]() такой, что
такой, что
![]() ;
;
б)пусть
![]() и множество
и множество
![]() не более чем одноточечно; тогда
не более чем одноточечно; тогда
![]()
в)пусть
![]() ; тогда для того, чтобы
; тогда для того, чтобы
![]() необходимо , чтобы множество
необходимо , чтобы множество
![]() было не более чем одноточечно.
было не более чем одноточечно.
Д о к а з а т е л ь с т в о. а). Пусть
![]() Для любого
Для любого
![]() имеем
wM = xM - xw,следовательно,
имеем
wM = xM - xw,следовательно,
![]() По теореме Хана-Банаха для любого
По теореме Хана-Банаха для любого
![]() найдется функционал
найдется функционал
![]() такой, что
такой, что
![]()
По лемме 3(а) множество
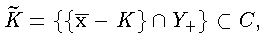 следовательно,
f касается
следовательно,
f касается
![]() в точке
в точке
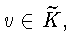 тогда
тогда
Пусть теперь существует функционал
![]() такой, что
такой, что
![]() По лемме 3(а)
По лемме 3(а)
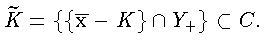 Имеем
Имеем
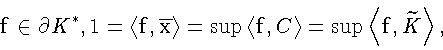
б). Пусть
![]() Как в предыдущем случае найдутся функционалы
Как в предыдущем случае найдутся функционалы
![]() ,
достигающие максимума на C в точках отрезков
,
достигающие максимума на C в точках отрезков
![]() и
и
![]() соответственно. В силу
соответственно. В силу ![]() справедливо
справедливо
![]() тогда
тогда
![]()
в). Пусть
![]()
Докажем, что
![]() .
По теореме
Хана-Банаха найдется некоторая замкнутая гиперплоскость H,
опорная к выпуклому телу
.
По теореме
Хана-Банаха найдется некоторая замкнутая гиперплоскость H,
опорная к выпуклому телу
![]() .
Имеем
.
Имеем
![]() следовательно,
следовательно,
![]() тогда
z = PH(x) и
тогда
z = PH(x) и
![]() Ясно, что
Ясно, что
![]() Имеем
Имеем
Следствие 1. Пусть X - линейное нормированное
пространство,
![]() Для того, чтобы M было множеством существования относительно Xнеобходимо и достаточно, чтобы для любого
x,где
Для того, чтобы M было множеством существования относительно Xнеобходимо и достаточно, чтобы для любого
x,где ![]() существовал функционал
существовал функционал
![]() такой, что
такой, что
![]()
Следствие 2. Пусть X - линейное нормированное
пространство,
![]() Для того, чтобы M было антипроксиминально относительно Xнеобходимо и достаточно, чтобы для любого
x,
Для того, чтобы M было антипроксиминально относительно Xнеобходимо и достаточно, чтобы для любого
x,
где ![]() не существовал функционал
не существовал функционал
![]() такой, что
такой, что
![]()
Теорема B [11].Пусть ![]() удовлетворяет условию Радона-Никодима, множество
удовлетворяет условию Радона-Никодима, множество
![]() выпукло и ограниченно, тогда
множество сильно* достигающих на M функционалов
выпукло и ограниченно, тогда
множество сильно* достигающих на M функционалов
![]() является плотным в
является плотным в
![]() множеством.
множеством.
Из леммы 5 и теоремы B (так как рефлексивное пространство
удовлетворяет условию Радона-Никодима) получаются два утверждения,
ранее доказанные в [3].
Следствие 3[3].Пусть
![]() .
Тогда EM является дополнением до множества первой категории
в
.
Тогда EM является дополнением до множества первой категории
в
![]() .
.
Следствие 4[3].Пусть
![]() .
Тогда TM является дополнением до множества первой
категории в
.
Тогда TM является дополнением до множества первой
категории в
![]() .
.
Лемма 6.Пусть X - банахово
пространство, а в X*найдется выпуклое замкнутое ограниченное центрально-симметричное тело
W такое, что
![]() -
-
![]() Тогда
Тогда
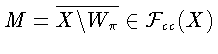 -
антипроксиминальное в X множество.
-
антипроксиминальное в X множество.
Д о к а з а т е л ь с т в о. Рассмотрим множество
![]() Множество N выпукло, ограниченно
и w*-замкнуто вместе с W.Пусть
Множество N выпукло, ограниченно
и w*-замкнуто вместе с W.Пусть
![]() Ясно, что
Ясно, что
![]() Имеем
Имеем
![]() -
-
![]() а поскольку
а поскольку
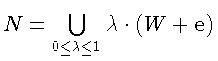 и
и
![]() то
то
![]() -
-
![]() По лемме 2
По лемме 2
![]()
Пусть
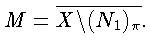 По лемме 4
По лемме 4
![]()
Докажем, что M антипроксиминально. Если найдется
![]() и
и
![]() то по лемме 5(а)
найдется функционал
то по лемме 5(а)
найдется функционал
![]() такой, что
такой, что
![]() Так как xM > 0, то
Так как xM > 0, то
![]() и
и
![]() Но,
Но,
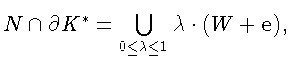 следовательно,
следовательно,
![]() противоречие, M антипроксиминально.
противоречие, M антипроксиминально.
Следствие 5.В бесконечномерном
пространстве
![]() существует центрально-симметричное антипроксиминальное
множество
существует центрально-симметричное антипроксиминальное
множество
![]() такое, что
такое, что
![]() ограниченно.
ограниченно.
О п р е д е л е н и е. Для
![]() обозначим
обозначим
![]()
Предложение 1.Пусть
![]() -конечна и
положительна и такая, что X бесконечномерно. Тогда в
-конечна и
положительна и такая, что X бесконечномерно. Тогда в
![]() найдется выпуклое замкнутое ограниченное центрально-симметричное тело
W такое, что
найдется выпуклое замкнутое ограниченное центрально-симметричное тело
W такое, что
![]() -
-
![]()
Д о к а з а т е л ь с т в о. Имеем
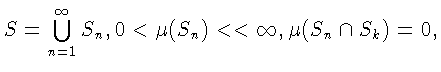 при
при
![]() Обозначим
S(X*) = SX*(0,1).Пусть
Обозначим
S(X*) = SX*(0,1).Пусть
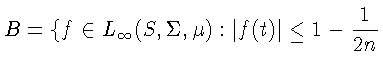 при
при
![]() Ясно, что
Ясно, что
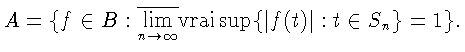
Как известно (см., например, [19, стр. 325]), для
![]() тогда
тогда
![]()
Пусть
W = w*-
![]() Ограниченность, выпуклость, w*-замкнутость и центральная симметрия W очевидны.
Ограниченность, выпуклость, w*-замкнутость и центральная симметрия W очевидны.
Имеем B = w*-
![]() -
-
![]() следовательно,
следовательно,
![]()
Для того, чтобы W было телом, достаточно , чтобы ему
принадлежали все функции из
VX*
(0,1/2), принимающие конечное
число значений (такие функции плотны в
![]() см. [12],
следствие 8,стр. 140). Пусть
см. [12],
следствие 8,стр. 140). Пусть
![]() и gпринимает значения
g1,g2,...,gm и
и gпринимает значения
g1,g2,...,gm и
![]() при
при ![]() Пусть
Пусть
![]() ясно что
ясно что
![]() Рассмотрим
Рассмотрим
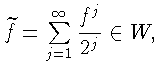 где
где
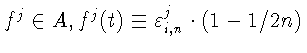 на Gi,n (не зависит от t на Gi,n),
на Gi,n (не зависит от t на Gi,n),
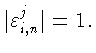 У нас
g(t) = gi при
У нас
g(t) = gi при
![]() следовательно,
следовательно,
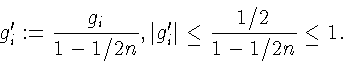
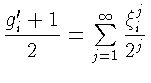 -
двоичное разложение
-
двоичное разложение
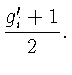 Тогда
Тогда