Теорема 4. Пусть
![]() следующие условия эквивалентны:
следующие условия эквивалентны:
а)X* строго выпукло;
б)всякое множество
![]() с
с
![]() выпукло;
выпукло;
б')всякое множество
![]() с
с
![]() выпукло;
выпукло;
в)всякое множество
![]() с
с
![]() выпукло;
выпукло;
в')всякое множество
![]() с
с
![]() выпукло.
выпукло.
Д о к а з а т е л ь с т в о. а)
![]() б). По
предложению 1.2 [5] M является
б). По
предложению 1.2 [5] M является ![]() солнцем, по
теореме 3.10 [7] M выпукло.
Импликации
б)
солнцем, по
теореме 3.10 [7] M выпукло.
Импликации
б)
![]() б')
б')
![]() в'),
б)
в'),
б)
![]() в)
в)
![]() в')
очевидны, так как
в')
очевидны, так как
![]() ([17], см. также [5, предложение 1.2]).
([17], см. также [5, предложение 1.2]).
в')
![]() а). Допустим, что
а). Допустим, что
![]() ,
тогда K* имеет двумерную грань
,
тогда K* имеет двумерную грань
![]() ,
где l1 и l2 экстремальные лучи конуса
K* ,
,
где l1 и l2 экстремальные лучи конуса
K* ,
![]()
![]()
![]() Очевидно, что
Очевидно, что
![]() Имеем
Имеем
![]() .
По лемме 3(д)
если
.
По лемме 3(д)
если
![]() и
и
![]() то
то
![]() при
при
![]() Следовательно,
для каждого
Следовательно,
для каждого
![]() функционал
функционал
![]() будет сильно* достигающим для
будет сильно* достигающим для
![]() По теореме 3(в)
По теореме 3(в)
![]() дифференцируема по Фреше на
дифференцируема по Фреше на
![]() Если M выпукло, то M - полупространство, тогда Nявляется отрезком,
g1 = g2 .
Если M выпукло, то M - полупространство, тогда Nявляется отрезком,
g1 = g2 .
З а м е ч а н и е .
Утверждение (а) Л.П.Власова содержится в импликации а)
![]() б ) теоремы 4, поскольку
б ) теоремы 4, поскольку
![]() ([#fit<#1510],
[5, предложение 1.2]), а утверждение (б) - это
импликация а)
([#fit<#1510],
[5, предложение 1.2]), а утверждение (б) - это
импликация а)
![]() в).
в).
О п р е д е л е н и е. Выпуклое замкнутое тело M банахова
пространства X называется гладким, если в каждой точке
![]() только один линейный непрерывный функционал
только один линейный непрерывный функционал
![]() достигает максимума
достигает максимума
на M.
Выпуклое замкнутое тело
![]() называется
строго выпуклым относительно банахова пространства Z, если
для каждого
называется
строго выпуклым относительно банахова пространства Z, если
для каждого
![]() множество
множество
![]() не более чем одноточечно.
не более чем одноточечно.
О п р е д е л е н и е. Будем писать
![]() ,
если
,
если
![]() и
существует замкнутое подпространство Z такое, что
фактор-пространство X/Z сепарабельно,
и
существует замкнутое подпространство Z такое, что
фактор-пространство X/Z сепарабельно,
![]()
З а м е ч а н и е . Известно, что класс (Ban) довольно
широк, в частности, он включает все сепарабельные и все
рефлексивные банаховы пространства X с
![]() а вопрос, охватывает ли он
все бесконечномерные банаховы пространства, является известной
проблемой Банаха.
а вопрос, охватывает ли он
все бесконечномерные банаховы пространства, является известной
проблемой Банаха.
Лемма 11. Пусть банахово пространство
![]() сепарабельно,
сепарабельно,
![]() Тогда в Y существует центрально-симметричное выпуклое множество
Тогда в Y существует центрально-симметричное выпуклое множество
![]() такое, что для
такое, что для
![]() и
и
![]() справедливы следующие утверждения:
справедливы следующие утверждения:
а)
![]() - гладкое компактное множество;
- гладкое компактное множество;
б)A - строго выпуклое относительно Y тело в Y* ;
г)существует последовательность функционалов
![]() таких, что
таких, что
![]()
д)
![]()
Д о к а з а т е л ь с т в о. а). В сепарабельном пространстве Xсуществует полная линейно независимая система
![]() тогда система
тогда система
![]() где
x0 =
e = (0,1),будет полной линейно независимой в
пространстве Y.Возьмем выпуклое гладкое центрально-симметричное компактное
множество
где
x0 =
e = (0,1),будет полной линейно независимой в
пространстве Y.Возьмем выпуклое гладкое центрально-симметричное компактное
множество
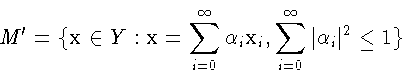
б) следует из определения поляры.
г). Так как для n > 1 точка
![]() то
по теореме об отделимости найдутся функционалы
то
по теореме об отделимости найдутся функционалы
![]() такие, что
такие, что
![]()
д).
![]() так как
так как
![]()
Теорема 5.Пусть
![]() Следующие условия эквивалентны:
Следующие условия эквивалентны:
а)в X есть ограниченное замкнутое гладкое выпуклое тело;
б)существует множество
![]() такое,
что
такое,
что
![]() , а
, а
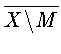 -
ограниченное выпуклое тело и
-
ограниченное выпуклое тело и
![]() одноточечно.
одноточечно.
Д о к а з а т е л ь с т в о. б)
![]() а).
По лемме 2 [6]
таким гладким ограниченным выпуклым телом будет множество
Q(b), где
а).
По лемме 2 [6]
таким гладким ограниченным выпуклым телом будет множество
Q(b), где
![]() .
.
а)
![]() б).
Возьмем ограниченное
замкнутое гладкое выпуклое тело W в
б).
Возьмем ограниченное
замкнутое гладкое выпуклое тело W в
![]() Пусть
Пусть ![]() - функционал Минковского, соответствующий множеству W.Положим
- функционал Минковского, соответствующий множеству W.Положим
![]() Имеем
Имеем
![]() - ограниченное гладкое замкнутое
выпуклое тело в Y. Тогда
- ограниченное гладкое замкнутое
выпуклое тело в Y. Тогда ![]() строго выпукло относительно Y.
строго выпукло относительно Y.
В силу условия
![]() найдется замкнутое
подпространство
найдется замкнутое
подпространство
![]() такое, что X/L сепарабельно. Считая
L подпространством в Y, видим,
что
такое, что X/L сепарабельно. Считая
L подпространством в Y, видим,
что
![]() и Y/Lсепарабельно. Возьмем
и Y/Lсепарабельно. Возьмем
![]() - множество из леммы 11.
Пусть
- множество из леммы 11.
Пусть
![]() - прообраз множества
- прообраз множества
![]() при отображении
пространства
Y в Y/L, где точке
при отображении
пространства
Y в Y/L, где точке
![]() ставится в соответствие
множество
y + L, пусть
ставится в соответствие
множество
y + L, пусть
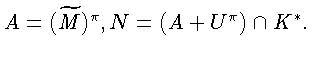 Множества A и
K* w*-замкнуты,
а
Множества A и
K* w*-замкнуты,
а ![]() - w*-бикомпакт, следовательно, N w*-замкнуто.
По лемме 11(д)
- w*-бикомпакт, следовательно, N w*-замкнуто.
По лемме 11(д)
![]() тогда в силу включения
тогда в силу включения
![]() получаем,
что N ограниченно и, следовательно, N w*-бикомпактно.
получаем,
что N ограниченно и, следовательно, N w*-бикомпактно.
Докажем, что
![]() .
Включение
.
Включение ![]() очевидно. Обозначим
очевидно. Обозначим
![]() .
Допустим, что существует
.
Допустим, что существует
![]() Множество D w*-замкнуто,
следовательно,
найдутся точка
Множество D w*-замкнуто,
следовательно,
найдутся точка
![]() и число
и число
![]() такие, что
такие, что
![]() Имеем
Имеем
![]() где
где
![]() По лемме 11 для множества
По лемме 11 для множества
![]() найдутся функционалы
найдутся функционалы
![]() такие, что
такие, что
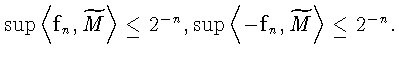 Рассмотрим последовательности
Рассмотрим последовательности
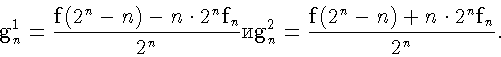
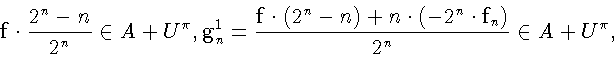
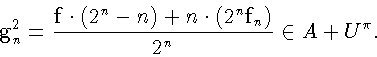
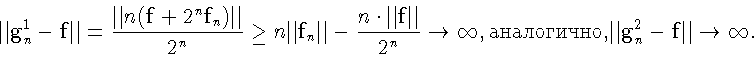
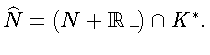 По лемме 2
По лемме 2

Докажем, что для любой точки
![]() такой, что
такой, что
![]() и
и
![]() множество
множество
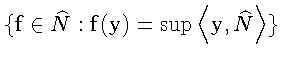 одноточечно.
Для этого достаточно доказать, что для любой точки
одноточечно.
Для этого достаточно доказать, что для любой точки
![]() такой, что
такой, что
![]() и
и
![]() множество
множество
![]() одноточечно,
действительно, для любого
одноточечно,
действительно, для любого ![]() имеем
имеем
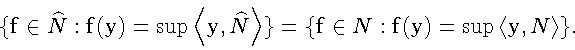
Множество N w*-бикомпактно,
следовательно, множество
![]() не пусто. Допустим, что существуют точка
не пусто. Допустим, что существуют точка
![]() и функционалы
и функционалы
![]() такие, что
такие, что
![]() Имеем
Имеем
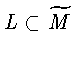 следует, что
следует, что
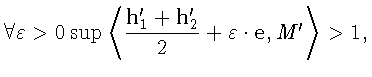 то
то
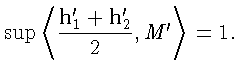 Тогда
Тогда
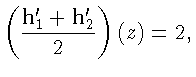 следовательно,
следовательно,
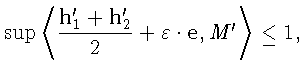 т.е.
т.е.
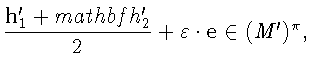 тогда
тогда
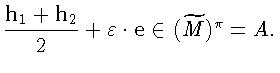 Тогда
Тогда
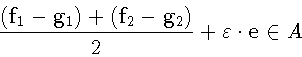
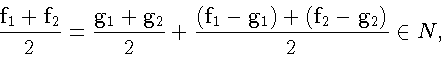
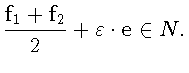 Имеем
Имеем
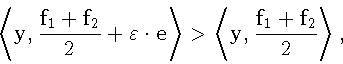
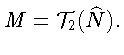 Поскольку в качестве
y можно взять (x,xM) для любого
Поскольку в качестве
y можно взять (x,xM) для любого
Теорема 6. Пусть
![]() Следующие условия
эквивалентны:
Следующие условия
эквивалентны:
а)X имеет эквивалентную гладкую норму;
б)в X существует множество
![]() такое,
что
такое,
что
![]() а
а
![]() -
ограниченное центрально-симметричное выпуклое тело и
-
ограниченное центрально-симметричное выпуклое тело и
![]() одноточечно.
одноточечно.
Д о к а з а т е л ь с т в о. б)
![]() а). В качестве
нового единичного шара возьмем множество
а). В качестве
нового единичного шара возьмем множество
![]() где
где
![]() Ясно, что Q(b) - ограниченное замкнутое
центрально-симметричное выпуклое тело, следовательно, перенормировка
эквивалентная. По лемме [21, стр. 22] в каждой точке из
Ясно, что Q(b) - ограниченное замкнутое
центрально-симметричное выпуклое тело, следовательно, перенормировка
эквивалентная. По лемме [21, стр. 22] в каждой точке из
![]() опорна только одна гиперплоскость, тогда (см.,
например, [13, стр. 24]) новая норма гладкая.
опорна только одна гиперплоскость, тогда (см.,
например, [13, стр. 24]) новая норма гладкая.
Доказательство импликации а)
![]() б)
получается повторением доказательства импликации а)
б)
получается повторением доказательства импликации а)
![]() б) в теореме 5, если в качестве множества Wвзять новый единичный шар в X такой, что перенормировка будет эквивалентной и новая
норма будет гладкой в X.
б) в теореме 5, если в качестве множества Wвзять новый единичный шар в X такой, что перенормировка будет эквивалентной и новая
норма будет гладкой в X.
Следствие 9.Пусть
![]() Если выполняется одно из условий:
а)Xрефлексивно;
б)X сепарабельно;
в)X* сепарабельно;
г)X - WCG-пространство;
д)X* - WCG-пространство;
е)
Если выполняется одно из условий:
а)Xрефлексивно;
б)X сепарабельно;
в)X* сепарабельно;
г)X - WCG-пространство;
д)X* - WCG-пространство;
е)
![]() то в X существует множество
то в X существует множество
![]() такое, что
такое, что
![]() а
а
![]() - ограниченное
центрально-симметричное выпуклое тело и
- ограниченное
центрально-симметричное выпуклое тело и
![]() одноточечно.
одноточечно.
Доказательство следствия получается из теоремы 6, так
как при выполнении любого из условий а) -
д) пространство
![]() и допускает эквивалентную
гладкую перенормировку.
и допускает эквивалентную
гладкую перенормировку.
О п р е д е л е н и е. (A*)[соответственно, ![]() ]
- класс
сопряженных пространств X*, в которых из условий
]
- класс
сопряженных пространств X*, в которых из условий
![]() [соответственно,
[соответственно,
![]() и того, что последовательность fn сходится к f в w*-топологии
пространства X*, следует, что fn сходится
к f по норме пространства X* .
3
и того, что последовательность fn сходится к f в w*-топологии
пространства X*, следует, что fn сходится
к f по норме пространства X* .
3
Лемма 12, возможно, известная, показывает, что условие
![]()
![]() не влечет
не влечет
![]()
Лемма 12.
![]() но
но
![]()
Д о к а з а т е л ь с т в о. Пусть
![]() последовательность
fn сходится к f в c0-топологии
пространства l1. Пусть существует число
последовательность
fn сходится к f в c0-топологии
пространства l1. Пусть существует число
![]() такое, что
такое, что
![]() Найдется номер k0 такой, что
Найдется номер k0 такой, что
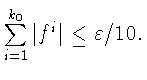 Из w* -сходимости последовательности fnполучаем, что существует номер n0 такой, что
Из w* -сходимости последовательности fnполучаем, что существует номер n0 такой, что
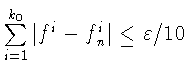 при
при
![]() Имеем
Имеем
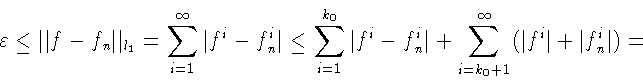
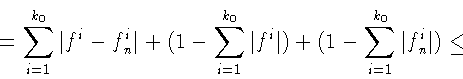
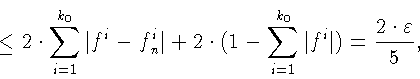
Для доказательства утверждения
![]() достаточно
взять
достаточно
взять
f = (1,1,1,...,1,1,...) и
fn =
(1,1,1,...,1,0,0,...) (n первых единиц), для
![]() надо взять функционалы
f,fn с
надо взять функционалы
f,fn с
![]() и
и
![]()
Предложение 2.Пусть
![]() Следующие условия эквивалентны:
Следующие условия эквивалентны:
а)
![]()
б)для любого множества
![]() справедливо равенство
справедливо равенство
![]()
в)для любого множества
![]() такого, что
такого, что
![]() ограниченно,
справедливо равенство
ограниченно,
справедливо равенство
![]()
Д о к а з а т е л ь с т в о. а)
![]() б). Включение
б). Включение
![]() очевидно.
Пусть
очевидно.
Пусть
![]() По теореме
3(б) функционал
По теореме
3(б) функционал
![]() достигает максимума на N в единственной точке
достигает максимума на N в единственной точке
![]() Если
функционал
Если
функционал
![]() не является сильно* достигающим, то найдется
последовательность
не является сильно* достигающим, то найдется
последовательность
![]() По лемме 3(в)
По лемме 3(в)
![]() следовательно, можно считать,
что
следовательно, можно считать,
что
![]() Последовательность
fnпринадлежит бикомпакту N, следовательно, относительно
бикомпактна, тогда последовательность
fn имеет w*-предельные точки. Пусть
Последовательность
fnпринадлежит бикомпакту N, следовательно, относительно
бикомпактна, тогда последовательность
fn имеет w*-предельные точки. Пусть
![]() - w*-предельная
точка для последовательности
fn . Ясно, что
- w*-предельная
точка для последовательности
fn . Ясно, что
![]() В силу условия
В силу условия
![]() тогда
тогда
![]() и
и
![]() Итак,
Итак, ![]() -
единственная w*-предельная точка для
последовательности
fn в w*-топологии пространства
Y*, тогда
-
единственная w*-предельная точка для
последовательности
fn в w*-топологии пространства
Y*, тогда
![]() сходится к
сходится к ![]() в w*-топологии
пространства Y* . Ясно, что fn сходится к
f в w* -топологии пространства X*, а
в w*-топологии
пространства Y* . Ясно, что fn сходится к
f в w* -топологии пространства X*, а
![]() В силу условия
В силу условия
![]() получаем, что
получаем, что
![]() следовательно,
следовательно,
![]() По теореме 3(в)
По теореме 3(в)
![]()
б)
![]() в) очевидно.
в) очевидно.
в)
![]() а). Допустим, что
а). Допустим, что
![]() т.е.
существуют точки
т.е.
существуют точки
![]() и число
и число
![]() такие, что
fn сходится к f в w*-топологии пространства X* и
такие, что
fn сходится к f в w*-топологии пространства X* и
![]() Пусть
Пусть
![]() Ясно, что
fn сходится к
f в
w*-топологии пространства Y*. Тогда множество
Ясно, что
fn сходится к
f в
w*-топологии пространства Y*. Тогда множество
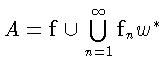 -замкнуто. Пусть
-замкнуто. Пусть
![]() Ясно, что
Ясно, что
![]() ограниченно, следовательно, N - бикомпакт
в w*-топологии пространства Y* . Для
y = (0,1)имеем
ограниченно, следовательно, N - бикомпакт
в w*-топологии пространства Y* . Для
y = (0,1)имеем
![]() для любого
для любого
![]() по теореме 3(б)
по теореме 3(б)
![]() Но,
fn сходится к
f в w*
-топологии пространства Y*, а
Но,
fn сходится к
f в w*
-топологии пространства Y*, а
![]() следовательно,
можно считать, что
следовательно,
можно считать, что
![]() а тогда
а тогда
![]()
О п р е д е л е н и е. (SA) - класс пространств, в которых условия
![]() -
-
![]() влекут соотношение
влекут соотношение
![]() (Л.П.Власов
[7,8])
(Л.П.Власов
[7,8])
Предложение 3.Пусть
![]() Следующие условия эквивалентны:
Следующие условия эквивалентны:
а)
![]()
б)
![]() справедливо
включение
справедливо
включение
![]()
в)
![]() такого, что
такого, что
![]() ограниченно,
справедливо включение
ограниченно,
справедливо включение
![]()
Д о к а з а т е л ь с т в о. а)
![]() б). Пусть
б). Пусть
![]() В
силу
В
силу
![]() можем считать, что
можем считать, что
![]() Пусть
Dn = zn + K. Имеем
Пусть
Dn = zn + K. Имеем
![]() следовательно, по лемме 3(а)
следовательно, по лемме 3(а)
![]() По теореме Хана-Банаха найдется функционал
По теореме Хана-Банаха найдется функционал
![]() разделяющий Dn и
int C. Тогда
разделяющий Dn и
int C. Тогда
![]() Можем считать, без потери общности, что
Можем считать, без потери общности, что
![]() У нас
У нас
![]() следовательно,
следовательно,
![]() В силу
В силу
![]() можем
считать, что
можем
считать, что
![]() Имеем
Имеем
![]() Так как
Так как
![]() то по теореме 3(б)
то по теореме 3(б)
![]() достигает
максимума на N в единственой точке и эта точка принадлежит
достигает
максимума на N в единственой точке и эта точка принадлежит
![]() следовательно,
следовательно,
![]() Имеем
Имеем
![]() следовательно,
следовательно,
![]() Из соотношения
Из соотношения
![]() получаем,
что
получаем,
что
![]() В силу
В силу
![]() получаем, что
получаем, что
![]() следовательно,
следовательно,
![]()
б)
![]() в), поскольку из
в), поскольку из
![]() вытекает
вытекает
![]() где
где
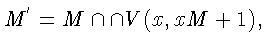 а из
а из
![]() вытекает
вытекает
![]()
б)
![]() а). Если в качестве множества
а). Если в качестве множества
![]() взять произвольное замкнутое
полупространство, то
взять произвольное замкнутое
полупространство, то
![]() следовательно, по теореме Джеймса
следовательно, по теореме Джеймса
![]()
Осталось доказать, что
![]() Допустим
противное, тогда в силу
Допустим
противное, тогда в силу
![]() существуют
последовательности
существуют
последовательности
![]() точка
точка
![]() и число
и число
![]() такие, что
такие, что
![]() По
функционалам
По
функционалам
![]() где
где
![]() и
и
![]() построим
множества
построим
множества
![]() и
и
![]() из предложения 2. Как в
предложении 2, получаем , что
из предложения 2. Как в
предложении 2, получаем , что
![]() для
для
![]() Имеем
Имеем
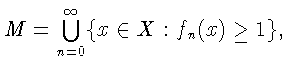 следовательно,
следовательно,
![]() Так как
y = (0,xM)достигает максимума на N только в одной точке f, то
Так как
y = (0,xM)достигает максимума на N только в одной точке f, то
![]() Имеем
Имеем
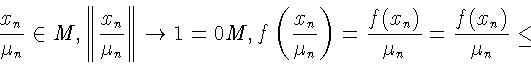
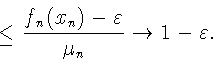
З а м е ч а н и е . В предложении 3 условие
![]() является существенным. Так, в
пространстве X последовательностей
является существенным. Так, в
пространстве X последовательностей
![]() суммируемых с квадратом, с нормой
суммируемых с квадратом, с нормой
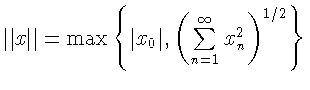 имеем
имеем
![]() но если положить
но если положить
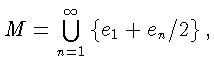 то
то
![]()
Предложение 4.Пусть
![]() Следующие условия эквивалентны:
Следующие условия эквивалентны:
а)
![]()
б)
![]() справедливо равенство
справедливо равенство
![]()
в)
![]() такого, что
такого, что
![]() ограниченно,
справедливо равенство
ограниченно,
справедливо равенство
![]()
Д о к а з а т е л ь с т в о совпадает с доказательством предложения
2, только функционал f будет принадлежать
![]()
Лемма 13.Пусть
![]() выпукло,
выпукло,
![]() Тогда для любого
Тогда для любого
![]() справедливо равенство
справедливо равенство
З а м е ч а н и е .
В случае ![]() лемма 13 доказана В.Кли [22].
В лемме условие выпуклости множества
нельзя отбросить. В качестве примера можно взять
лемма 13 доказана В.Кли [22].
В лемме условие выпуклости множества
нельзя отбросить. В качестве примера можно взять
![]() (евклидова плоскость), а M - дополнение до квадрата.
(евклидова плоскость), а M - дополнение до квадрата.
С помощью этой леммы из предложений 2 и 4 вытекают следствия 10 и 11.
Следствие 10. Пусть
![]() Следующие условия эквивалентны:
Следующие условия эквивалентны:
а)
![]()
б)для любого выпуклого множества
![]() справедливо равенство
справедливо равенство
![]()
Следствие 11.Пусть
![]() Следующие условия эквивалентны:
Следующие условия эквивалентны:
а)
![]()
б)для любого выпуклого множества
![]() справедливо равенство
справедливо равенство
![]()
Поступила 16.02.96