Е. Ф. Леликова
Исследуется поведение при 
фундаментального решения
(ФР) G(x,s,t) задачи Коши для параболического уравнения
t>0. Предполагается,
что для
коэффициентов
b(x),
a(x)
при 
справедливы
представления вида
где функции
в свою очередь, при разлагаются в
асимптотические ряды по положительным степеням 
и
Построено и обосновано асимптотическое
разложение ФР G(x,s,t) при с точностью до любой
степени 
для всей плоскости 
фундаментального
решения (ФР) G(x,s,t) задачи Коши для параболического
уравнения
и
при 
разлагаются
в асимптотические ряды вида
при 
и представление, аналогичное представлению (0.3), справедливо
и для функции 
. Кроме того, предполагается выполненным
условие
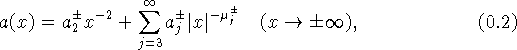
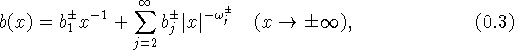
A)Уравнение 
не имеет
нетривиальных решений из 
при
действительных
Результатом работы является построение и обоснование
асимптотического разложения G(x,s,t) при с
точностью до любой степени равномерно относительно всех
.
Всюду в дальнейшем ограничимся изучением случая, когда
коэффициент 
поскольку уравнение (0.1) может быть
сведено к уравнению, не содержащему члена с первой
производной, при помощи замены 
Учитывая соотношения (0.2), (0.3), нетрудно получить, что в
результате такой замены коэффициент при новой неизвестной
функции v(x,t) по-прежнему разлагается в асимптотические
ряды вида (0.2).
Итак, рассматривается задача
Предполагается, что выполнено условие A) и коэффициент
a(x)
при разлагается в асимптотические ряды вида (0.2).
Очевидно, что условие A) выполнено, если 
Однако, легко построить примеры, когда это условие
выполнено и для знакопеременного коэффициента a(x). Однако
"главный" коэффициент 
не может быть большим
отрицательным: из условия A) вытекает неравенство
(см., например, [1], с.150).
Будем считать, что все степени 
в разложении (0.2)
целые, т.е. оно имеет вид
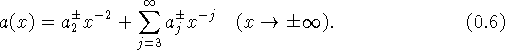
Это ограничение не является существенным, исследование в
случае произвольных 
может быть проведено
совершенно аналогично.
Рассматриваемая здесь скорость убывания коэффициента
a(x) играет особую роль. Она является критической в
следующем смысле: в случае более медленного убывания
G(x,s,t)
убывает при сверхстепенным образом (см. [2]), а в
случае более быстрого убывания 
ФР G(x,s,t) при ведет
себя аналогично ФР уравнения теплопроводности (см. [3]).
Поведение при ФР G(x,s,t) определенным образом
связано с поведением при решений однородного
стационарного уравнения
Будем говорить, что это уравнение принадлежит к первому
типу, если оно имеет такие линейно независимые решения
, что
В противном случае легко показать, что рассматриваемое
уравнение имеет такие линейно независимые решения , что
При выполнении условия (0.8) будем говорить, что
стационарное уравнение принадлежит ко второму типу.
Для того, чтобы описать показатели степеней, по
которым будут построены асимптотические разложения,
рассмотрим алгебраические уравнения
являющиеся определяющими для уравнений Эйлера
соответствующих стационарному уравнению при 
Корни
этих уравнений всюду в дальнейшем будем обозначать через
, 
. Они имеют вид
и при любых значениях коэффициента
удовлетворяющих неравенству (0.5), эти корни
действительны, различны при 
, а при
существует
двукратный корень 
. Обозначим 
Тип стационарного уравнения, величины 
, а также соотношения между ними, и определяют
показатели степеней в асимптотических разложениях G(x,s,t) при
. В случае, когда 
, т.е.
, где 
- целое
неотрицательное,
асимптотическое разложение G(x,s,t) при построено
и обосновано для уравнений первого типа в работе [4], а для
уравнений второго типа - в работе [5]. Кроме того, краткое
изложение результатов для уравнений обоих типов содержится
в работе [6].
В данной работе исследуется случай, когда выполнено
хотя бы одно из равенств: 
где - целое
неотрицательное.
Метод построения асимптотических разложений
G(x,s,t) подробно описан в работе [4] и состоит в
следующем. От функции G(x,s,t) перейдем к еë преобразованию
Лапласа 
. При выполнении условия A) функция
аналитична в области 
и является в
этой области решением задачи
Точка 
является особой точкой функции ,
и поведение функции при 
определяет
поведение функции G(x,s,t) при . Поэтому для решения
поставленной задачи достаточно исследовать поведение
решения в окрестности точки .
Пусть 
- комплексная плоскость с разрезом вдоль
действительной отрицательной полуоси:
и через
обозначена ветвь
многозначной функции такая, что 
Определим в
области функции 
, 
-
решения однородного
уравнения 
такие, что
Известно, что функции 
существуют и аналитичны в
области (см., например, [7], с.320). С помощью этих функций
легко строится :
где через 
обозначен вронскиан решений 
,
, и исследование поведения
в окрестности
особой точки сводится к исследованию поведения
решений при 
Так же, как и в
работах [3], [4], для этой цели используется метод согласования
асимптотических разложений [8], [9].
План данной статьи следующий. В § 1 формулируются и
доказываются некоторые вспомогательные утверждения, с
помощью которых строятся формальные асимптотические решения
(ФАР) задач для функций ,
, в § 2
описывается
процесс построения этих ФАР, в § 3 в соответствии с
формулой (0.12) строится асимптотическое разложение функции
при 
которое затем обосновывается. В
§ 4
содержатся основные теоремы об асимптотике G(x,s,t) при
. Поскольку данная работа в определенном смысле
является продолжением работ [3], [4], то доказательства тех
или иных утверждений, аналогичных доказанным в этих
работах, будут опускаться. Конец доказательства, а также
того или иного утверждения (теоремы, леммы, замечания),
когда оно приводится без доказательства, обозначается
символом .
при
при