2. Построение формального асимптотического разложения решений при

1. Внешнее разложение решения при При больших по модулю отрицательных x асимптотическое разложение функции будем строить как при уравнения удовлетворяющее первому из условий (0.11) и имеющее вид

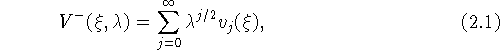
Учитывая соотношение (0.6), для определения коэффициентов получаем систему уравнений

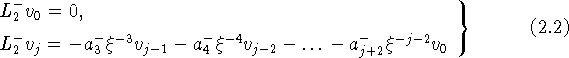
и условия

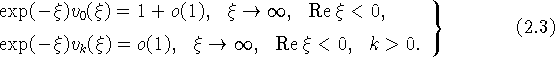
Теорема 2.1. Существуют функции - единственные решения системы (2.2), удовлетворяющие условиям (2.3). В области для них справедливы оценки

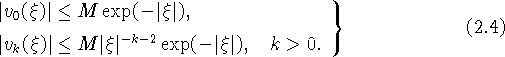
Аналогичные оценки справедливы и для производных функций .

При функции разлагаются в асимптотические ряды вида:

где





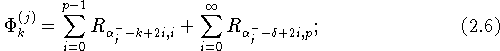
где



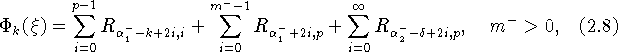
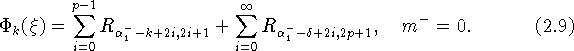
Здесь , при при k=2r+1. Ряды допускают почленное дифференцирование.

Доказательство этой теоремы совершенно аналогично доказательству теоремы 2.1 работы [3]. Решение можно выписать явно. Действительно, нетрудно проверить, что имеет вид ([11, стр.139]). При k>0 решение строится методом вариации постоянных. Оценки (2.4) для решений могут быть легко получены из явных формул.

Что же касается асимптотических представлений (2.5), (2.7), то для k=0 они легко получаются из асимптотических формул для функций Бесселя, а для k>0 доказательство проводится по индукции с использованием соответствующих явных представлений для решений и соотношений (1.1) леммы 1.1.

2. Внутреннее разложение решения Перейдем к построению асимптотического разложения функции в центральной области, т.е. для не слишком больших по абсолютной величине значений x. Для того, чтобы выяснить вид асимптотической последовательности в этой области, воспользуемся полученной выше информацией о поведении уже построенного разложения (2.1) при Заменим коэффициенты их асимптотическими представлениями (2.5), (2.7) и перейдем в этих представлениях от переменной к переменной . После несложных преобразований получим:

при

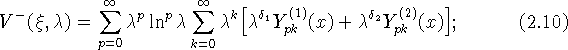
при

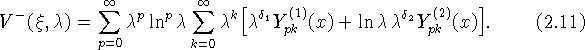
Здесь обозначено при ; ряды где при при .

В соответствии со структурой представлений (2.10), (2.11) асимптотическое разложение решения при в центральной области будем строить в виде:

при

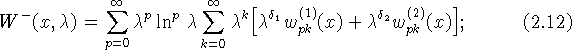
при

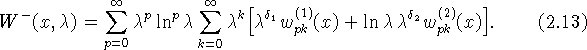
Для определения коэффициентов получаем рекуррентные системы уравнений:

Кроме того, функции должны удовлетворять условиям согласования

где асимптотические ряды определены представлениями (2.10), (2.11).

Теорема 2.2. Существуют функции - решения уравнений (2.14), удовлетворяющие условиям (2.15).

Д о к а з а т е л ь с т в о. Нетрудно проверить, что ряды в представлениях (2.10), (2.11) являются при той же самой системы уравнений (2.2), что и искомые функции (это следует из того, что ряд (2.1) является при уравнения а ряды (2.5), (2.7) являются краевых задач для коэффициентов ряда (2.1)). Поэтому естественно, что существуют решения уравнений (2.14), обладающие заданной асимптотикой (2.15). Достаточно при построении функций лишь позаботиться о том, чтобы были выполнены условия первой леммы единственности (леммы 1.2).

Реализуется это следующим образом. Фиксируем некоторое На каждом k-м шаге построим общее решение уравнений (2.14) в виде

где w(x) - какое-нибудь частное решение соответствующего неоднородного уравнения, а - выбранные линейно независимые решения однородного уравнения , - некоторые неопределенные константы. Это общее решение имеет при асимптотическое представление Используя соотношение (1.9) замечания 1.2, нетрудно выписать специальное представление вида (1.3) как для ряда , так и для ряда , определяемого соотношениями (2.10), (2.11). Сравнивая эти специальные представления, выберем константы таким образом, чтобы были выполнены условия первой леммы единственности (леммы 1.2). При этом ряды и совпадут, и тем самым искомое решение будет построено.

Рассмотрим эту процедуру несколько подробнее. Предположим, что . Пусть j=1, . Положим

и рассмотрим ряд . Согласно замечанию 1.2 к лемме 1.2 этот ряд имеет вид (определение ряда см. в § 1, (1.6)), и следовательно, для выполнения условий леммы 1.2 достаточно выбрать

Перейдем к функциям . Построим какое-нибудь частное решение уравнения (2.14). Например, его можно выписать методом вариации постоянных, используя решения , . Нетрудно проверить, что при справедливо представление

где асимптотический ряд , - некоторая постоянная. Положим

где постоянную надлежит определить. Очевидно, что для так выбранного решения справедливо соотношение

Воспользуемся теперь леммой 1.2. Специальное представление (1.3) для ряда имеет вид

где - постоянная, определяемая выбором частного решения . Для ряда аналогичное представление имеет вид

Ряды и совпадают, если выбрать так, чтобы Функция построена, остальные функции при строятся аналогично.

Пусть теперь j=2. Положим

и рассмотрим ряд . Согласно замечанию 1.2 этот ряд имеет вид

С другой стороны, из соотношений (1.8) следует, что

при . Следовательно, для выполнения условий первой леммы единственности достаточно выбрать

Функция построена. Построение функций при ничем не отличается от построения функций для .

В случае, когда построение функций проводится аналогично вышепроведенному. При этом для при фиксированном старшие члены по-прежнему задаются соотношениями вида (2.17), (2.18), а при необходимо в соответствии с условиями согласования (2.15) положить

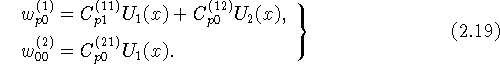
Построение коэффициентов проведено, теорема 2.2 доказана.

Следующие пять лемм содержат описание асимптотического поведения построенных решений при

Лемма 2.1. Пусть Тогда для функций при справедливо асимптотическое представление вида



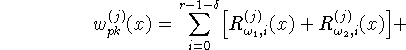
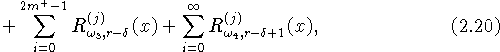
где . Величина определяется следующим образом. При j=2 положим При j=1 для уравнений первого типа , для уравнений второго типа Функции для i<0. Асимптотическое представление (2.20) допускает почленное дифференцирование.

Лемма 2.2. Пусть Тогда для функций при справедливо асимптотическое представление вида

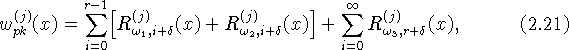
где . Величина определяется следующим образом. При j=2 положим При j=1 для уравнений первого типа , для уравнений второго типа Функции для l<0. Асимптотическое представление (2.21) допускает почленное дифференцирование.

Лемма 2.3. Пусть Тогда для функций - коэффициентов внутреннего разложения, при справедливо асимптотическое представление вида (2.20), где для j=1,2.

Лемма 2.4. Пусть Тогда для функций - коэффициентов внутреннего разложения, при справедливо асимптотическое представление вида (2.21), где для j=1,2.

Лемма 2.5. Пусть . Тогда для функций - коэффициентов внутреннего разложения, при справедливо асимптотическое представление вида (2.22), где для j=1,2.

Доказательство всех этих пяти лемм проводится по одной и той же схеме. Для старших членов , задаваемых формулами (2.17)-(2.19), справедливость асимптотических представлений (2.20), (2.21) при вытекает из соотношений (1.5), (1.7), (1.8) для решений . Для других k (при данном фиксированном p) доказательство проводится по индукции. Сначала выписывается общий вид асимптотического представления построенного решения в котором отслеживаются только порядки функций образующих его. Затем с помощью соотношения (1.2) уточняются значения показателей Лемма 2.1 доказана.

Остальные леммы (леммы 2.2-2.5) доказываются совершенно аналогично. Те несущественные различия, которые имеются в конкретном виде асимптотических представлений (2.20), (2.21), вызваны с одной стороны различием в виде асимптотических представлений для решений при различных , а с другой стороны - различием в поведении при для уравнений первого и второго типов.

3. Внешнее разложение решения при При построении асимптотического разложения решения для больших положительных x вновь воспользуемся принципом согласования асимптотических разложений. Заменим в разложениях (2.12), (2.13) коэффициенты соответствующими из асимптотических представлений (2.20), (2.21) и перейдем в получившихся соотношениях от переменной x к переменной . В результате этой процедуры внутреннее разложение примет вид:

для

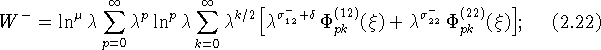
для

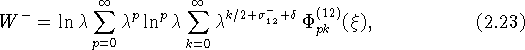
где обозначено . В этих представлениях для уравнений первого типа, для уравнений второго типа; при при Асимптотические ряды удовлетворяют соотношениям

где

Представления (2.22), (2.23) можно объединить в одно, записав их в виде

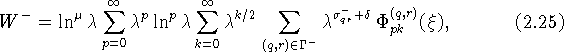
где обозначено . Множество определяется следующим образом:

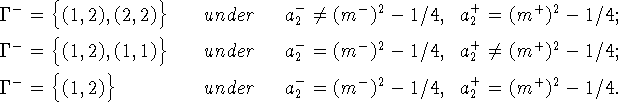
Здесь при (q,r)=(1,2) и для всех остальных пар . Величина определена выше: при при . Асимптотические ряды удовлетворяют соотношениям (2.24).

Следовательно, асимптотическое разложение функции при и больших положительных x нужно строить в виде

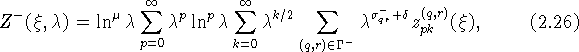
где множество и величины и определены выше.

Нетрудно выписать уравнения для определения коэффициентов
. Эти уравнения такие же, как уравнения (2.2), с той лишь разницей, что вместо оператора рассматривается оператор

Итак,

К этим уравнениям следует присоединить условия на поведение функций при

где - асимптотические ряды из представления (2.25).

Теорема 2.3. Существуют функции - решения системы
(2.27), удовлетворяющие условиям (2.28). При для них выполнены оценки

и аналогичные оценки выполнены и для производных этих функций.

Доказательство этой теоремы не отличается от доказательства предыдущей теоремы и основывается на том, что ряды являются при тех же самых уравнений (2.27), что искомые функции . Поэтому при построении достаточно лишь следить за выполнением условий второй леммы единственности (леммы 1.3).

Решение строится в виде где - какое-нибудь частное решение неоднородного уравнения (2.27), а - решения однородного уравнения определенные в § 1 (см. (1.11)), - некоторые неопределенные константы. Это общее решение имеет при асимптотическое представление . Используя соотношение (1.15) замечания 1.3 и асимптотические представления (1.13), (1.14) для решений , нетрудно выписать специальное представление вида (1.10) как для ряда , так и для ряда , определенного соотношением (2.25). Сравнивая эти специальные представления, выберем константы таким образом, чтобы были выполнены условия второй леммы единственности (леммы 1.3). При этом ряды и совпадут, и тем самым искомое решение будет построено.

Пусть, например, (q,r)=(1,2). Положим и для выбора константы C обратимся к ряду . Согласно замечанию 1.3 к лемме 1.3 для этого ряда имеет место соотношение

где - ряд, определенный в (1.14). Поэтому следует положить C=b.

Перейдем к функции . Построим какое-нибудь частное решение неоднородного уравнения (2.28). Нетрудно убедиться в том, что при это решение разлагается в сумму асимптотических рядов

где ряд Чтобы исключить присутствие членов вида в разложении строящегося решения при положим

так что Константу C определим из условия согласования. Для этого запишем ряд в специальном виде (1.10):

Здесь - некоторая константа, определяемая выбором частного решения . Рассмотрим далее ряд из соотношения (2.28) и также запишем его в виде (1.10):

Оба ряда и являются при одного и того же уравнения

Поэтому для их совпадения в силу второй леммы единственности (леммы 1.3) достаточно выбрать постоянную C из условия . Функция построена. Другие функции строятся аналогично.

Оценки (2.29) для функций нетрудно получить, воспользовавшись явными формулами для частного решения однородного уравнения (2.27). Теорема доказана. Построение формальных асимптотических разложений решения при закончено.

4. Построение для функции Совершенно аналогичным образом, только в зеркальном отражении, строится асимптотическое разложение решения , и поэтому ограничимся лишь кратким описанием этого процесса.

Внешнее разложение. Построение начинается с больших положительных x, разложение строится в виде

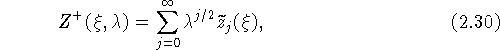
где коэффициенты являются в области решениями уравнений (2.27) и удовлетворяют условиям

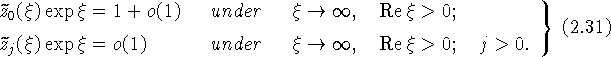
Для функций справедливы (с заменой области на область утверждения теоремы 2.1 и лемм 2.1, 2.2, в частности, при они разлагаются в асимптотические ряды вида (2.5), (2.7).

Внутреннее разложение. Воспользовавшись асимптотикой коэффициентов при точно так же, как в п. 2 данного параграфа, построим внутреннее разложение:

при

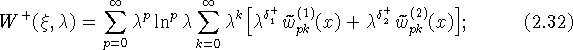
при

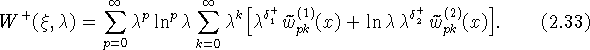
Здесь обозначено при Это асимптотическое разложение согласовано с внешним разложением (2.30). Коэффициенты определяются как решения систем (2.14), обладающие заданным поведением (вида (2.15)) при , и задаются соотношениями вида (2.16). Для них справедливы утверждения, аналогичные утверждениям теоремы 2.2 и лемм 2.1-2.5.

Ограничимся лишь тем, что приведем вид старших членов асимптотических разложений (2.30), (2.32).

Для уравнений первого типа условия согласования диктуют следующий выбор:

для

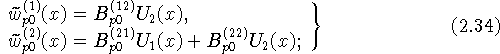
для

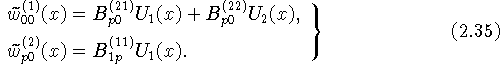
Для уравнений второго типа решения выбираются следующим образом:

для

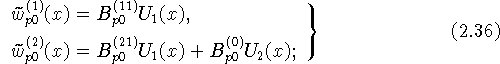
для

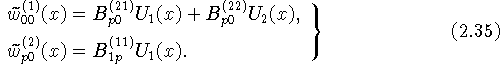
Наконец, используя для коэффициентов асимптотические представления вида (2.20), (2.21) при , построим внешнее разложение в виде

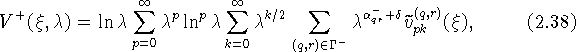
где Величины и множество пар определяются так же, как в соотношении (2.26). Коэффициенты - это решения системы (2.2), имеющие заданную асимптотику (вида (2.28)) при . Для них справедливы утверждения, аналогичные утверждениям теоремы 2.3. Построение формальных асимптотических разложений решений при закончено.