4. Асимптотика ФР G(x,s,t) при

После того, как асимптотика в окрестности особой точки построена, остается, обращая преобразование Лапласа, воспользоваться стандартным способом получения асимптотического разложения G(x,s,t) - решения задачи (0.4) при из асимптотики при (см., например, [12]). Асимптотика построена для всех , следовательно, и асимптотическое разложение также может быть получено для всей плоскости x, s. Очевидно, что коэффициенты асимптотики G(x,s,t) будут иметь различный вид в разных частях плоскости x, s. Наиболее интересной и содержательной является асимптотика в центральной части плоскости (x,s) - области

и поэтому мы ограничимся формулировкой результатов лишь для этой области. Структура асимптотики в других частях плоскости x,s описана в работе [3] (теорема 3.1).

Обозначим (напомним, что - корни определяющего уравнения Эйлера (0.9)), через N обозначим достаточно большое натуральное число. Главные члены асимптотических разложений будут приведены при x<s.

Теорема 4.1. Пусть стационарное уравнение принадлежит к первому типу, и хотя бы для одного из коэффициентов выполнено соотношение , где - целое положительное. Тогда для G(x,s,t) при в области справедливо асимптотическое представление

Здесь при при - достаточно большое натуральное число, ; функция является конечной суммой слагаемых вида .

Д о к а з а т е л ь с т в о. Выпишем вид построенной в предыдущем параграфе функции в центральной части плоскости (область определена равенством (3.1)). Согласно формулам (3.2), (3.3), (3.5)

где - вронскиан функций .

Предположим для определенности, что ( Непосредственное вычисление вронскиана с использованием формул (2.13), (2.32) дает





где

С другой стороны, равенство (3.4) означает, что для не слишком больших



где при , и

Выделим главный член представления (4.3). По построению (см. (2.17), (2.18), (2.34))



Следовательно, в представлениях (4.2), (4.3) главным членом является

так что

Нетрудно проверить и справедливость следующего представления:







Теперь уже из равенств (4.4), (4.5) легко получить, что в области справедливо представление

сумма конечна.

Дальнейшее доказательство проводится по стандартной схеме. Применим формулу обращения преобразования Лапласа

где - решение задачи (0.10), а - прямая Так как аналитична в области и для нее справедлива оценка (3.6), то можно деформировать контур в контур , состоящий из двух лучей:

Для интеграла по той части , где в силу (3.6) справедлива экспоненциальная оценка. Он по модулю не больше, чем А интеграл по представим в виде

Заменяя в первом интеграле функцию ее представлением (4.6) и используя оценку (3.7) для второго интеграла, приходим к асимптотическому представлению (4.1) для G(x,s,t) при .

Совершенно аналогично рассматриваются случаи, когда либо , либо . Теорема доказана.

Интересно выписать главный член асимптотики G(x,s,t) при в рассматриваемом случае. Им является функция

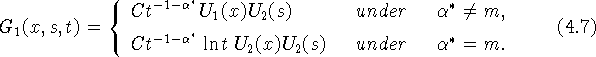
Теорема 4.2. Пусть стационарное уравнение принадлежит к первому типу и коэффициент . Тогда для G(x,s,t) при в области справедливо асимптотическое представление

Здесь - некоторые функции такие, что

где при функция является конечной суммой слагаемых вида

Д о к а з а т е л ь с т в о. Так же, как и при доказательстве предыдущей теоремы, выпишем представление для частичной суммы .

Рассматриваемая ситуация соответствует случаю кратного корня
определяющего уравнения В этом случае внутреннее разложение имеет вид (2.13).

Пусть для определенности т.е. внутреннее разложение имеет тот же вид (2.32), что и в случае, рассмотренном в предыдущей теореме.

Непосредственной проверкой можно убедиться в том, что



где - вронскиан соответствующих частичных сумм, - полином от y степени

Обратимся теперь к формулам (2.19), (2.34), определяющим старшие коэффициенты , , внутренних разложений . В рассматриваемом случае

а , имеют тот же вид, что и в предыдущей теореме. Следовательно,

Обозначим и перепишем в виде



Нетрудно проверить, что соотношение (4.2) принимает вид



где функция - конечная сумма слагаемых вида .

Заменяя в этом равенстве функцию ее представлением (4.11), получаем для



где

Аналогично тому, как это было сделано в предыдущей теореме, используя получившееся представление (4.12) функции при обращении преобразования Лапласа, приходим к представлению (4.8) для G(x,s,t). Нетрудно проверить, что для получающихся при этом функций действительно имеют место соотношения (4.9).

Главный член асимптотики в данном случае имеет вид

где , функция определена соотношением (4.13), а через V(y) обозначен интеграл Рамануджана ([13])

Нетрудно проверить, что при , следовательно, . Теорема доказана.

В случае, когда и стационарное уравнение принадлежит к первому типу, справедлива теорема, аналогичная теореме 4.2, с заменой в (4.8) показателя на

З а м е ч а н и е 4.1. Из только что доказанных теорем, а также из теоремы 3.1 работы [4], в которой построено асимптотическое разложение G(x,s,t) в случае, когда , следует, что для уравнений первого типа при всех допустимых значениях "главных" коэффициентов асимптотических разложений (0.6) скорость убывания G(x,s,t) при больше, чем скорость убывания 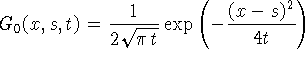уравнения теплопроводности. Минимальная скорость убывания при этом отвечает случаю, когда хотя бы один из коэффициентов имеет минимальное значение, что равносильно существованию кратного корня соответствующего определяющего уравнения.

Рассмотрим теперь случай, когда стационарное уравнение относится к уравнениям второго типа. Справедлива

Теорема 4.3. Пусть стационарное уравнение является уравнением
второго типа и Тогда для G(x,s,t) при в области справедливо асимптотическое представление

Здесь - некоторые функции такие, что

где при

Доказательство этой теоремы аналогично доказательству предыдущих теорем и мы ограничимся его кратким описанием.

Для внутреннего разложения в данном случае по-прежнему следует пользоваться формулами (2.13), а для счета его старших коэффициентов - формулами (2.19). Можно проверить, что главным членом вронскиана при является где и соответственно, для частичной суммы при справедливо представление вида

где - некоторая постоянная.

Отсюда уже легко получается асимптотическое представление (4.15) для G(x,s,t) и соотношения (4.16) для функций . Теорема 4.3 доказана.

Аналогичный результат имеет место и в случае, когда

Главным членом асимптотического представления в данном случае (когда хотя бы одна из разностей корней определяющих уравнений равна 2, а другая не меньше 2) является функция

где через V(y) обозначен интеграл Рамануджана ([13])

а - некоторая постоянная. Нетрудно проверить, что при и следовательно, для фиксированных G(x,s,t) при убывает медленно:

Работа выполнена при финансовой поддержке фонда РФФИ N 96-01-00501.

Поступила 29.06.95

СПИСОК ЦИТИРОВАННОЙ ЛИТЕРАТУРЫ

1. Глазман И.М. Прямые методы качественного спектрального анализа сингулярных дифференциальных операторов.- М.: Ф.М., 1963.- 336 с.
2. Яфаев Д.Р. Сверхстепенное убывание по времени решений уравнения Шредингера // Докл. АН СССР.- 1984.- T.258, N. 4.- C.850-853.
3. Леликова Е.Ф. Асимптотика фундаментального решения параболического уравнения при // Матем. сб.- 1987.- T.132, N. 3.- C.322-344.
4. Леликова Е.Ф. Об асимптотике фундаментального решения параболического уравнения в критическом случае // Матем. сб.- 1989.- T.180, N. 8.- C.1119-1130.
5. Леликова Е.Ф. Об асимптотике фундаментального решения параболического уравнения второго порядка // Матем. сб.- 1995.- T.186, N. 4.- C.125-142.
6. Леликова Е.Ф. Об асимптотике фундаментального решения параболического уравнения в критическом случае // Докл. РАН.- 1995.- T.341, N. 5.- C.532-535.
7. Наймарк М.А. Линейные дифференциальные операторы.- М.: Наука, 1969.- 528 с.
8. Ван-Дайк М. Методы возмущений в механике жидкости.- М.: Мир, 1967.- 310 с.
9. Ильин А.М. Согласование асимптотических разложений решений краевых задач.- М.: Наука, 1989.- 336 с.
10. Коддингтон Э.А., Левинсон Н. Теория обыкновенных дифференциальных уравнений.- М.: ИЛ, 1958.- 474 с.
11. Лебедев Н.Н. Специальные функции и их приложения.- М.,Л.: Ф.М., 1960.- 358 с.
12. Олвер Ф. Асимптотика и специальные функции.- М.: Наука, 1990.- 528 c.
13. Hardy G.H. Ramanujan.- Cambridge, 1940.