Пусть ![]() , m - целое
неотрицательное. Через
, m - целое
неотрицательное. Через
![]()
![]() будем
обозначать функции вида
будем
обозначать функции вида
![]() , где
, где ![]() - одна
из ветвей многозначной
функции
- одна
из ветвей многозначной
функции ![]() - одна из ветвей многозначной функции
- одна из ветвей многозначной функции
![]() - полином степени m. Число
- полином степени m. Число ![]() будем называть порядком функции
будем называть порядком функции ![]() . В случаях,
когда нет необходимости следить за значением индекса m, второй
индекс у введенных функций будем опускать.
. В случаях,
когда нет необходимости следить за значением индекса m, второй
индекс у введенных функций будем опускать.
Лемма 1.1. Для любой функции ![]() существует
функция
существует
функция
![]() такая, что
такая, что
![]()
При этом p=q, если ![]() не является корнем определяющего
уравнения (0.9); p=q+i, если
не является корнем определяющего
уравнения (0.9); p=q+i, если ![]() является i-кратным
корнем определяющего уравнения
является i-кратным
корнем определяющего уравнения ![]() .
.
Доказательство леммы легко вытекает из соотношения
![]()
![]()
![]()
и того, что 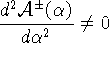 для
любых
для
любых
![]() (максимальная
кратность корня определяющего уравнения равна 2).
(максимальная
кратность корня определяющего уравнения равна 2).
З а м е ч а н и е 1.1.
Если ![]() , то функция
, то функция ![]() определяется уравнением (1.1) однозначно. В противном
случае она имеет вид
определяется уравнением (1.1) однозначно. В противном
случае она имеет вид
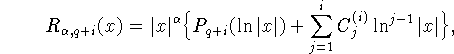
где i - кратность корня (i=1,2), полином ![]() определяется уравнением (1.1) однозначно и значение t=0
является i-кратным корнем полинома
определяется уравнением (1.1) однозначно и значение t=0
является i-кратным корнем полинома ![]()
![]() -
произвольные постоянные.
-
произвольные постоянные.
Множество асимптотических при ![]() рядов вида
рядов вида
![]()
где ![]() - целое,
- целое, ![]() ,
будем обозначать через
,
будем обозначать через
![]() . Фиксировав некоторое
. Фиксировав некоторое ![]() , выделим
подмножество
асимптотических рядов
, выделим
подмножество
асимптотических рядов ![]() , старшие члены которых
имеют
порядок
, старшие члены которых
имеют
порядок ![]() . Наряду с Y(x) будем использовать для элементов
множеств
. Наряду с Y(x) будем использовать для элементов
множеств ![]() обозначения
обозначения ![]() . Иногда, если это не
будет вызывать недоразумений, мы будем писать просто
. Иногда, если это не
будет вызывать недоразумений, мы будем писать просто ![]() вместо
вместо ![]() .
.
В дальнейшем мы будем иметь дело с классами ![]() такими,
что
такими,
что ![]() , где
, где ![]() - корни
определяющего уравнения
(0.9), m - целое неотрицательное. Иногда будет удобно
использовать некоторое специальное представление для ряда
- корни
определяющего уравнения
(0.9), m - целое неотрицательное. Иногда будет удобно
использовать некоторое специальное представление для ряда
![]() выделяя в нем слагаемые, являющиеся
решениями
однородного уравнения
выделяя в нем слагаемые, являющиеся
решениями
однородного уравнения ![]() , т.е. записывая ряд Y(x) в
виде
, т.е. записывая ряд Y(x) в
виде
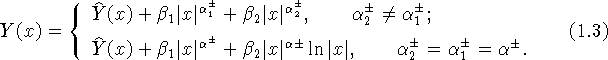
Здесь через ![]() обозначен такой асимптотический ряд, у
которого все слагаемые порядков
обозначен такой асимптотический ряд, у
которого все слагаемые порядков ![]() имеют множители вида
имеют множители вида
![]() где
где ![]() для
для ![]() для
для ![]() При этом, вообще
говоря, ряд
При этом, вообще
говоря, ряд
![]() , где
, где
![]() .
.
В классе рядов ![]() будем рассматривать уравнение
будем рассматривать уравнение
![]() , понимая под решением этого уравнения при
, понимая под решением этого уравнения при
![]() . Нетрудно показать, что для любого
. Нетрудно показать, что для любого ![]() и любого
ряда
и любого
ряда ![]() существует множество
рядов
существует множество
рядов
![]() являющихся
уравнения
являющихся
уравнения ![]() при
при
![]() . Для построения таких достаточно
воспользоваться утверждением леммы 1.1. Из замечания 1.1
следует, что при
. Для построения таких достаточно
воспользоваться утверждением леммы 1.1. Из замечания 1.1
следует, что при ![]() , где m - целое
неотрицательное,
множество
, где m - целое
неотрицательное,
множество ![]() бесконечно, но справедлива
бесконечно, но справедлива
Лемма 1.2 первая лемма единственности. Пусть
![]()
![]() , ряд
, ряд ![]() , где
, где ![]() , а ряды
, а ряды
![]() и являются
уравнения
и являются
уравнения ![]() при
при ![]() . Если в специальных представлениях (1.3) этих
рядов
. Если в специальных представлениях (1.3) этих
рядов ![]() для всех входящих в это
представление
слагаемых, то
для всех входящих в это
представление
слагаемых, то
![]()
Рассмотрим однородное уравнение ![]() Фиксируем линейно независимые решения
Фиксируем линейно независимые решения ![]() этого уравнения, удовлетворяющие одному из условий
(0.7), (0.8). Нетрудно проверить (см., например,
[10], гл. V), что для выбранной ФСР
этого уравнения, удовлетворяющие одному из условий
(0.7), (0.8). Нетрудно проверить (см., например,
[10], гл. V), что для выбранной ФСР
![]() имеют
место соотношения
имеют
место соотношения
1) Для уравнений первого типа
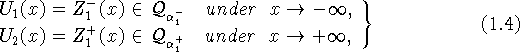
где
![]()
при всех значениях коэффициента ![]() ;
;

где ряды ![]() ряды
ряды
![]() те же, что и в соотношениях
(1.4),
те же, что и в соотношениях
(1.4), ![]() - некоторые постоянные.
- некоторые постоянные.
2) Для уравнений второго типа
![]()
где
![]()
![]()
где ряды ![]() ряды
ряды
![]() определены соотношением
(1.6),
определены соотношением
(1.6), ![]() - некоторые константы.
- некоторые константы.
Нетрудно привести и более конкретный вид рядов ![]() ,
соответствующих большему корню
,
соответствующих большему корню ![]() определяющего
уравнения (0.9):
определяющего
уравнения (0.9):
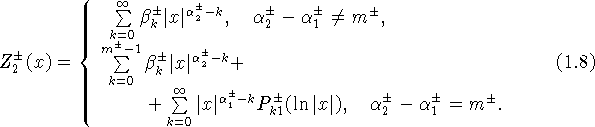
Здесь ![]() - целое неотрицательное,
- целое неотрицательное, ![]()
З а м е ч а н и е 1.2.
Если ряд ![]() и является при
и является при
![]() уравнения
уравнения ![]() , то он имеет вид
, то он имеет вид
![]()
где асимптотический ряд ![]() определяется рассматриваемым
уравнением однозначно, а
определяется рассматриваемым
уравнением однозначно, а ![]() - некоторые
постоянные.
- некоторые
постоянные.
2. Через ![]() всюду в дальнейшем будем обозначать
всюду в дальнейшем будем обозначать
![]() , где параметр
, где параметр ![]() ,
область
,
область ![]() и ветвь
многозначной функции
и ветвь
многозначной функции ![]() определены во введении.
определены во введении.
Множество асимптотических при ![]() рядов вида
рядов вида
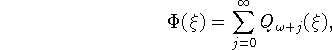
где ![]() , будем обозначать через
, будем обозначать через
![]() Фиксировав некоторое
Фиксировав некоторое
![]() , выделим подмножество
, выделим подмножество ![]() асимптотических рядов, старшие
члены которых имеют порядок
асимптотических рядов, старшие
члены которых имеют порядок ![]() . Наряду с
. Наряду с ![]() будем
использовать для элементов множества
будем
использовать для элементов множества ![]() обозначения
обозначения
![]() ,
, ![]() .
.
Пусть ![]() , где
, где ![]() ,
, ![]() - целое
неотрицательное. Легко проверить, что специальное
представление вида (1.3), т.е. представление, в котором
выделены слагаемые, являющиеся решениями однородного
уравнения
- целое
неотрицательное. Легко проверить, что специальное
представление вида (1.3), т.е. представление, в котором
выделены слагаемые, являющиеся решениями однородного
уравнения ![]() принимает вид
принимает вид
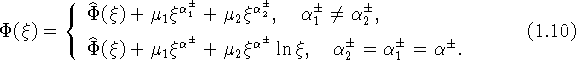
Через ![]() здесь обозначен ряд, у которого все слагаемые
порядка
здесь обозначен ряд, у которого все слагаемые
порядка ![]() (j=1,2) имеют множители вида
(j=1,2) имеют множители вида
![]() , где
, где ![]() для
для ![]() для
для
![]() . При этом,
вообще говоря, ряд
. При этом,
вообще говоря, ряд ![]() , где
, где
![]()
Обозначим 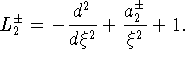 В классе рядов
В классе рядов ![]() будем рассматривать уравнение
будем рассматривать уравнение ![]() , понимая под
решением этого уравнения при
, понимая под
решением этого уравнения при ![]() соответственно. Нетрудно проверить, что для любого ряда
соответственно. Нетрудно проверить, что для любого ряда
![]() существует множество рядов
существует множество рядов
![]() являющихся уравнения
являющихся уравнения ![]() при
при ![]() Для
построения таких достаточно воспользоваться
утверждением леммы 1.1. Из замечания 1.1 следует, что при
Для
построения таких достаточно воспользоваться
утверждением леммы 1.1. Из замечания 1.1 следует, что при
![]() , где m - целое неотрицательное,
множество
, где m - целое неотрицательное,
множество
![]() бесконечно, но справедлива
бесконечно, но справедлива
Лемма 1.3 вторая лемма единственности. Пусть ряд
![]()
![]() , где
, где ![]() а ряды
а ряды
![]() и являются при
и являются при
![]() одного и
того же уравнения
одного и
того же уравнения ![]() . Если в
представлениях (1.10)
этих рядов
. Если в
представлениях (1.10)
этих рядов ![]() для всех входящих в
это представление слагаемых, то
для всех входящих в
это представление слагаемых, то
![]()
Рассмотрим однородное уравнение ![]() в областях
в областях
![]() соответственно. Нетрудно проверить, что
решением этого уравнения является функция
соответственно. Нетрудно проверить, что
решением этого уравнения является функция ![]() где
где ![]()
![]() - решение
уравнения Бесселя. Положим
- решение
уравнения Бесселя. Положим
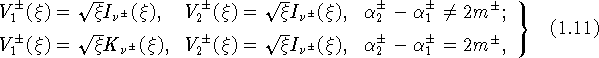
где ![]() - модифицированные
функции Бесселя.
Функции
- модифицированные
функции Бесселя.
Функции ![]()
![]() являются линейно
независимыми
решениями уравнения
являются линейно
независимыми
решениями уравнения ![]() и для них справедливы
асимптотические представления вида
и для них справедливы
асимптотические представления вида
![]()
При этом (см., например, [11]) для ![]() , где
, где ![]() -
целое неотрицательное, ряды
-
целое неотрицательное, ряды ![]() имеют вид
имеют вид
![]()
а для ![]() ряд
ряд ![]() имеет вид
имеет вид
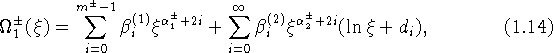
а ряд ![]() по-прежнему имеет вид (1.13).
по-прежнему имеет вид (1.13).
З а м е ч а н и е 1.3.
Если ряд ![]() и является при
и является при ![]() уравнения
уравнения ![]() то он
имеет вид
то он
имеет вид
![]()
где ряд ![]() и определяется рассматриваемым
уравнением однозначно,
и определяется рассматриваемым
уравнением однозначно, ![]() - ряды
(1.12), а
- ряды
(1.12), а ![]() - некоторые константы.
- некоторые константы.