при 
Используя частичные суммы формальных рядов (2.1),
(2.12), (2.13), (2.26), (2.30), (2.32), (2.33), (2.38),
построим асимптотическое разложение решения задачи
(0.10) при 
для всех 
. Для
асимптотического ряда
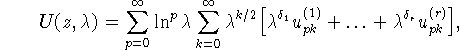
где 
, введем обозначение
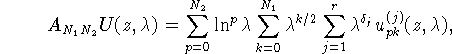
где 
- натуральные числа.
Рассмотрим области
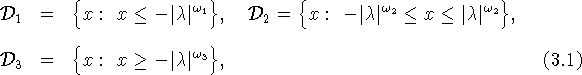
где 
и
определим в
каждой из этих областей функции 
следующим
образом:
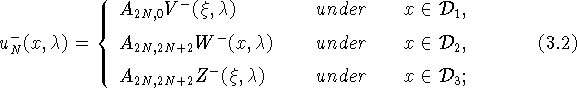
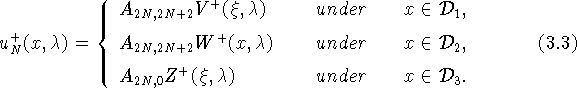
Обозначим через 
вронскиан функций 
.
Лемма 3.1. Для всех 
справедливо
представление
где 
не зависит от x.
Доказательство этой леммы полностью повторяет доказательство аналогичного утверждения для уравнений первого типа, приведенное в работе [3] (см. § 3).
Конкретный вид частичной суммы 
зависит от
значений "главных" коэффициентов 
в
асимптотическом
разложении (0.6) и будет приведен позднее. А пока в
соответствии с планом, изложенным во введении, продолжим
построение асимптотического представления фундаментального
решения при 
Положим в
соответствии с формулой (0.12)
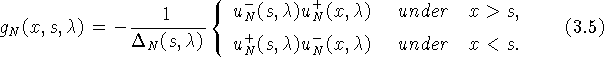
Функция 
- это на самом деле девять функций,
каждая из которых определена в области 
и является в этой области задачи
(0.10)
при По построению все эти функции согласованы в
общих частях областей 
, поэтому из них легко строится
(см., например, [3], § 4) функция 
, которая
определена уже для всех 
, совпадает
в каждой из
областей с построенной там функцией
и
является задачи (0.10) для всех при
Функция является асимптотическим
представлением
функции при Справедлива
Теорема 3.1.
В области 
для
функции - решения задачи (0.10), справедлива оценка
а в области 
- оценка
где - построенная выше функция, 
-
произвольно, а постоянные 
и M зависят от 
и не
зависят от x, s и 
.
Доказательство этой теоремы совершенно аналогично доказательству теоремы 3 работы [3].