Если ![]() пара вершин графа
пара вершин графа ![]() , которые находятся на расстоянии 2
друг от друга, то подграф на множестве общих смежных с ними вершин называется
, которые находятся на расстоянии 2
друг от друга, то подграф на множестве общих смежных с ними вершин называется
![]() -подграфом графа
-подграфом графа ![]() .
.
Графы без 3-лап с несвязными ![]() -подграфами
были изучены в 1994 году А.Е. Брауэром и М. Нуматой [7].
Теорема А.Е. Брауэра и М. Нуматы [7] утверждает, что конечными
графами без 3-лап, у которых все
-подграфами
были изучены в 1994 году А.Е. Брауэром и М. Нуматой [7].
Теорема А.Е. Брауэра и М. Нуматы [7] утверждает, что конечными
графами без 3-лап, у которых все ![]() -подграфы несвязны, являются
решетчатые
-подграфы несвязны, являются
решетчатые ![]() -графы и
-графы и ![]() -графы.
Пусть
-графы.
Пусть
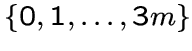 множество вершин
множество вершин ![]() -графа. Тогда
вершины
-графа. Тогда
вершины ![]() , где
, где ![]() , смежны в
, смежны в ![]() -графе тогда и только тогда, когда
-графе тогда и только тогда, когда
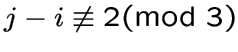 . Понятно, что
. Понятно, что ![]() -графы не содержат
-графы не содержат
![]() -коклик.
-коклик.
В графе с несвязными ![]() -подграфами
любой подграф, изоморфный
-подграфами
любой подграф, изоморфный ![]() , содержится в подграфе, изоморфном
, содержится в подграфе, изоморфном
![]() , то есть в
, то есть в ![]() . Такие графы мы будем называть
. Такие графы мы будем называть
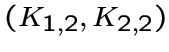 -однородными графами.
Следовательно, граф, у которого все
-однородными графами.
Следовательно, граф, у которого все ![]() -подграфы несвязны, является
-подграфы несвязны, является
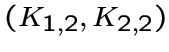 -однородным графом.
-однородным графом.
Следующая теорема, которая
обобщает теорему А.Е. Брауэра и М. Нуматы в том случае, когда граф
содержит ![]() -коклику, доказывается в первой главе диссертации [45].
Для того, чтобы сформулировать теорему, нам понадобится понятие
кликового расширения графа.
Кликовым расширением графа
-коклику, доказывается в первой главе диссертации [45].
Для того, чтобы сформулировать теорему, нам понадобится понятие
кликового расширения графа.
Кликовым расширением графа ![]() называется граф,
полученный заменой каждой вершины
называется граф,
полученный заменой каждой вершины ![]() из
из ![]() на полный
подграф
на полный
подграф 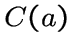 , содержащий не менее одной вершины, причем вершины
из различных клик
, содержащий не менее одной вершины, причем вершины
из различных клик 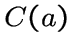 и
и 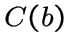 смежны тогда и только тогда,
когда вершины
смежны тогда и только тогда,
когда вершины ![]() и
и ![]() смежны в
смежны в ![]() .
Кликовое расширение графа
.
Кликовое расширение графа ![]() называется
называется
![]() -расширением
-расширением ![]() , если для любой вершины
, если для любой вершины ![]() подграф
подграф 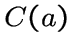 содержит
содержит ![]() вершин для некоторого фиксированного
вершин для некоторого фиксированного
![]() . Заметим, что если граф
. Заметим, что если граф ![]() не содержит 3-лап, то и
любое его кликовое расширение не содержит 3-лап.
не содержит 3-лап, то и
любое его кликовое расширение не содержит 3-лап.
Пусть связный граф ![]() содержит
содержит ![]() -коклику и не содержит
-коклику и не содержит ![]() -лап.
Если любой подграф из
-лап.
Если любой подграф из ![]() , изоморфный
, изоморфный ![]() , содержится в подграфе,
изоморфном
, содержится в подграфе,
изоморфном ![]() , то
, то
![]() является кликовым расширением одного из следующих графов:
является кликовым расширением одного из следующих графов:
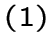 решетчатый
решетчатый ![]() -граф при
-граф при ![]() ,
, ![]() ;
;
 треугольный граф
треугольный граф 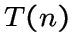 при
при ![]() ;
;
 граф Шлефли.
граф Шлефли.
Для удобства обозначим через ![]() класс графов, который состоит из
класс графов, который состоит из
![]() -графов при
-графов при ![]() ,
, ![]() ,
треугольных графов
,
треугольных графов 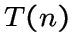 при
при ![]() и графа Шлефли.
В теореме 1 из работы [29] М. Нуматой была получена
классификация реберно-регулярных графов,
которые не содержат 3-лап и содержат
и графа Шлефли.
В теореме 1 из работы [29] М. Нуматой была получена
классификация реберно-регулярных графов,
которые не содержат 3-лап и содержат ![]() -коклику.
Оказалось, что если такой граф имеет диаметр 2,
то он является или графом из класса
-коклику.
Оказалось, что если такой граф имеет диаметр 2,
то он является или графом из класса ![]() или графом
или графом ![]() при
при ![]() ,
который имеет
,
который имеет ![]() вершин.
вершин.
Следующая теорема, которая является аналогом этого результата для кореберно-регулярных графов без 3-лап, также доказывается в первой главе диссертации [53].
Пусть ![]() -- кореберно-регулярный граф без
-- кореберно-регулярный граф без ![]() -лап.
Тогда
-лап.
Тогда ![]() является либо дополнительным графом к регулярному графу
без треугольников, либо
является либо дополнительным графом к регулярному графу
без треугольников, либо ![]() -расширением
-расширением
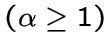 одного из
следующих графов:
одного из
следующих графов:
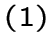 вполне несвязный граф с числом вершин
вполне несвязный граф с числом вершин ![]()
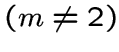 ;
;
 решетчатый
решетчатый ![]() -граф при
-граф при
![]() ;
;
 треугольный граф
треугольный граф 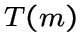 при
при ![]() ;
;
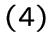 граф Шлефли.
граф Шлефли.
В теореме 2 работы [29] М. Нуматой получена классификация
реберно-регулярных графов диаметра не менее 3,
которые не содержат 3-лап и
содержат ![]() -коклику. Он показал, что либо все
-коклику. Он показал, что либо все ![]() -подграфы такого
графа имеют не более 2 вершин, либо граф изоморфен графу
икосаэдра.
-подграфы такого
графа имеют не более 2 вершин, либо граф изоморфен графу
икосаэдра.
Полученные результаты служат основой для исследования графов без 3-лап с более слабыми условиями регулярности во второй главе диссертации.
Пусть ![]() пара вершин графа
пара вершин графа ![]() , которые находятся на расстоянии 2
друг от друга. Обозначим число вершин
, которые находятся на расстоянии 2
друг от друга. Обозначим число вершин ![]() -подграфа для
-подграфа для ![]() через
через
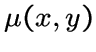 . Если все
. Если все ![]() -подграфы
графа
-подграфы
графа ![]() имеют одинаковое число вершин, то есть
имеют одинаковое число вершин, то есть 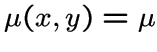 ,
то это число называется параметром
,
то это число называется параметром ![]() графа
графа ![]() .
Понятно, что если граф имеет параметр
.
Понятно, что если граф имеет параметр ![]() , то
, то ![]() не меньше 1.
Если граф
не меньше 1.
Если граф ![]() имеет параметр
имеет параметр ![]() , но его значение неизвестно,
то мы говорим, что
, но его значение неизвестно,
то мы говорим, что ![]() имеет равномощные
имеет равномощные ![]() -подграфы.
По определению сильного графа, любая пара несмежных вершин в нем имеет одно и
то же число общих соседей. Это условие автоматически приводит к тому, что
либо диаметр сильного графа равен 2 и он имеет равномощные
-подграфы.
По определению сильного графа, любая пара несмежных вершин в нем имеет одно и
то же число общих соседей. Это условие автоматически приводит к тому, что
либо диаметр сильного графа равен 2 и он имеет равномощные ![]() -подграфы,
либо число общих соседей любой пары несмежных вершин в нем равно 0.
Таким образом, условие равномощности
-подграфы,
либо число общих соседей любой пары несмежных вершин в нем равно 0.
Таким образом, условие равномощности ![]() -подграфов значительно
ослабляет соответствующее условие в определении сильного графа.
-подграфов значительно
ослабляет соответствующее условие в определении сильного графа.
Вторая глава диссертации посвящена классификации
графов без 3-лап с равномощными ![]() -подграфами без ограничения на диаметр
графа.
В первом параграфе главы 2 рассматриваются регулярные графы без 3-лап с
равномощными
-подграфами без ограничения на диаметр
графа.
В первом параграфе главы 2 рассматриваются регулярные графы без 3-лап с
равномощными ![]() -подграфами, а во втором параграфе исследуются
нерегулярные графы из этого класса.
Изучение класса графов без 3-лап с
равномощными
-подграфами, а во втором параграфе исследуются
нерегулярные графы из этого класса.
Изучение класса графов без 3-лап с
равномощными ![]() -подграфами самая трудная и большая по объему часть работы.
Оказалось, что сильное влияние на
строение графа оказывает наличие или отсутствие в графе порожденных 4-циклов.
Графы без 4-циклов с равномощными
-подграфами самая трудная и большая по объему часть работы.
Оказалось, что сильное влияние на
строение графа оказывает наличие или отсутствие в графе порожденных 4-циклов.
Графы без 4-циклов с равномощными ![]() -подграфами изучал П. Тервиллигер
в [38]. Он доказал реберную регулярность таких графов при некоторых
дополнительных условиях, в частности, для регулярных графов диаметра 2.
Графы без порожденных 4-циклов с равномощными
-подграфами изучал П. Тервиллигер
в [38]. Он доказал реберную регулярность таких графов при некоторых
дополнительных условиях, в частности, для регулярных графов диаметра 2.
Графы без порожденных 4-циклов с равномощными ![]() -подграфами мы будем
называть графами Тервиллигера.
-подграфами мы будем
называть графами Тервиллигера.
Следующая теорема классифицирует регулярные графы Тервиллигера без 3-лап [54].
ТЕОРЕМА 3.Связный регулярный граф Тервиллигера
без 3-лап является ![]() -расширением одного из следующих графов:
-расширением одного из следующих графов:
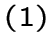 граф без
граф без ![]() -лап с
-лап с ![]() ,
,
 граф икосаэдра.
граф икосаэдра.
Примеры регулярных графов без 3-лап с ![]() имеются среди графов вершин и
ребер полуправильных многогранников. Граф усеченного тетраэдра
является
имеются среди графов вершин и
ребер полуправильных многогранников. Граф усеченного тетраэдра
является ![]() -регулярным с
-регулярным с ![]() , но не реберно-регулярным графом.
Граф кубооктаэдра, наоборот, является реберно-регулярным
графом без 3-лап, но не является
, но не реберно-регулярным графом.
Граф кубооктаэдра, наоборот, является реберно-регулярным
графом без 3-лап, но не является ![]() -регулярным графом.
В следующей теореме классифицированы связные
-регулярным графом.
В следующей теореме классифицированы связные ![]() -регулярные
графы без 3-лап [54].
-регулярные
графы без 3-лап [54].
Связный ![]() -регулярный граф
-регулярный граф ![]() без
без
![]() -лап либо является графом Тервиллигера, либо имеет диаметр
-лап либо является графом Тервиллигера, либо имеет диаметр ![]() .
.
Теперь строение связных ![]() -регулярных графов определяют теорема 2
и теорема 3, поскольку в них определены графы Тервиллигера без
-регулярных графов определяют теорема 2
и теорема 3, поскольку в них определены графы Тервиллигера без ![]() -лап
и кореберно-регулярные графы без 3-лап.
-лап
и кореберно-регулярные графы без 3-лап.
В следующей теореме мы не предполагаем регулярности графа, и, таким образом,
она завершает классификацию графов Тервиллигера без 3-лап [55].
Эта теорема расширяет теорему Тэйлора-Левингстона [37].
Через ![]() обозначим порожденный подграф, состоящий из вершины
обозначим порожденный подграф, состоящий из вершины ![]() и всех смежных с ней вершин.
Через
и всех смежных с ней вершин.
Через ![]() обозначим подграф
обозначим подграф
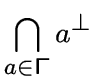 .
.
ТЕОРЕМА 5.Пусть ![]() -- связный граф
Тервиллигера без
-- связный граф
Тервиллигера без ![]() -лап. Тогда либо граф
-лап. Тогда либо граф ![]() является
является
![]() -расширением графа икосаэдра, либо
подграф на множестве всех вершин с некликовыми окрестностями из
-расширением графа икосаэдра, либо
подграф на множестве всех вершин с некликовыми окрестностями из
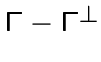 является пустым, кликой или
является пустым, кликой или ![]() -расширением связного
графа с
-расширением связного
графа с ![]() .
.
При условии, что граф содержит 3-коклику, удается получить полную
классификацию не только графов Тервиллигера без 3-лап, но и всех
графов без 3-лап с равномощными ![]() -подграфами [55].
-подграфами [55].
ТЕОРЕМА 6. Пусть ![]() -- связный граф без
-- связный граф без ![]() -лап,
содержащий
-лап,
содержащий ![]() -коклику. Пусть также все
-коклику. Пусть также все ![]() -подграфы из
-подграфы из ![]() имеют одинаковое число вершин.
Тогда либо
имеют одинаковое число вершин.
Тогда либо ![]() имеет диаметр больше двух и является графом
из заключения теоремы 5, либо граф
имеет диаметр больше двух и является графом
из заключения теоремы 5, либо граф ![]() является
является
![]() -расширением одного из следующих графов:
-расширением одного из следующих графов:
 решетчатый
решетчатый ![]() -граф при
-граф при ![]() ,
, ![]() ;
;
 треугольный граф
треугольный граф 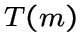 при
при ![]() ;
;
 граф Шлефли.
граф Шлефли.
Следующая теорема посвящена описанию графов
без 3-лап с регулярными ![]() -подграфами одинаковой ненулевой валентности.
Регулярный граф называется редуцированным,
если для любой вершины
-подграфами одинаковой ненулевой валентности.
Регулярный граф называется редуцированным,
если для любой вершины ![]() множество
множество
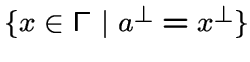 состоит из единственной вершины
состоит из единственной вершины ![]() .
В статье [27] А.А. Махнев перенес это понятие на класс всех графов.
Произвольный граф
.
В статье [27] А.А. Махнев перенес это понятие на класс всех графов.
Произвольный граф ![]() называется редуцированным,
если для любой вершины
называется редуцированным,
если для любой вершины ![]() множество
множество
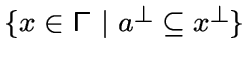 состоит из единственной вершины
состоит из единственной вершины ![]() .
Легко видеть, что в классе регулярных графов оба определения эквивалентны.
.
Легко видеть, что в классе регулярных графов оба определения эквивалентны.
В [27] А.А. Махнев классифицировал редуцированные графы без
3-лап с регулярными ![]() -подграфами валентности
-подграфами валентности ![]() , где
, где ![]() .
Мы докажем, что если
.
Мы докажем, что если ![]() является графом без 3-лап с регулярными
является графом без 3-лап с регулярными
![]() -подграфами одинаковой валентности
-подграфами одинаковой валентности ![]() , где
, где ![]() , и
для любой вершины
, и
для любой вершины ![]() из
из ![]() множество
множество
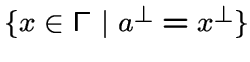 совпадает с
совпадает с
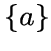 , то и множество
, то и множество
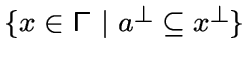 состоит из единственной вершины
состоит из единственной вершины ![]() . Следующая теорема [43,44]
усиливает основной результат из [27].
. Следующая теорема [43,44]
усиливает основной результат из [27].
Пусть ![]() -- связный граф, который
не содержит
-- связный граф, который
не содержит ![]() -лап и содержит
-лап и содержит ![]() -коклику и выполнены
следующие условия:
-коклику и выполнены
следующие условия:
![]() все
все ![]() -подграфы из
-подграфы из ![]() являются регулярными
графами одинаковой валентности
являются регулярными
графами одинаковой валентности ![]() для некоторого числа
для некоторого числа ![]() ;
;
![]() для любой вершины
для любой вершины ![]() множество
множество
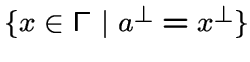 состоит из единственной вершины
состоит из единственной вершины ![]() .
.
Тогда граф ![]() является треугольным графом
является треугольным графом 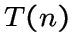 при
при ![]() ,
графом икосаэдра или графом Шлефли.
,
графом икосаэдра или графом Шлефли.
В работе [19] М.Д. Хестенс и Д.Г. Хигман отметили другой
момент, касающийся связи между теорией графов
и теорией транзитивных групп подстановок.
Пусть ![]() -- транзитивная группа подстановок на множестве
-- транзитивная группа подстановок на множестве ![]() .
Тогда орбиты группы
.
Тогда орбиты группы ![]() на множестве
на множестве
![]() называются орбиталами, а их число -- рангом группы
называются орбиталами, а их число -- рангом группы ![]() .
Каждый орбитал
.
Каждый орбитал ![]() является либо симметричным, либо строго
антисимметричным. В первом случае он
определяет обыкновенный граф с множеством вершин
является либо симметричным, либо строго
антисимметричным. В первом случае он
определяет обыкновенный граф с множеством вершин ![]() и множеством
ребер
и множеством
ребер ![]() . Во втором случае орбитал
имеет симметричную ему пару
. Во втором случае орбитал
имеет симметричную ему пару
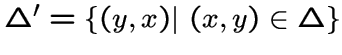 и
определяет ориентированный граф.
Известно, что группа
и
определяет ориентированный граф.
Известно, что группа ![]() обладает
симметричным орбиталом тогда и только тогда, когда ее порядок является
четным числом [40].
обладает
симметричным орбиталом тогда и только тогда, когда ее порядок является
четным числом [40].
Если группа ![]() имеет ранг 3, то оба орбитала, отличные от диагонали
имеет ранг 3, то оба орбитала, отличные от диагонали
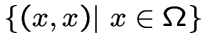 , являются симметричными и
определяют пару дополнительных сильно регулярных
графов. Такой сильно регулярный граф называется графом ранга 3.
В настоящее время с использованием классификации конечных простых групп
получено полное описание групп и графов ранга 3 ([9],
[25], [2], [26], [24]).
, являются симметричными и
определяют пару дополнительных сильно регулярных
графов. Такой сильно регулярный граф называется графом ранга 3.
В настоящее время с использованием классификации конечных простых групп
получено полное описание групп и графов ранга 3 ([9],
[25], [2], [26], [24]).
Много работ посвящено изучению транзитивных групп
подстановок без ограничений на их ранг и графов, которые определяются
их орбиталами.
В программном комплексе GAP [32] имеется специальная инструкция
EdgeOrbitGraph, которая позволяет строить граф по орбиталу заданной
транзитивной группы подстановок. При помощи этой
инструкции автором найден пример дистанционно-транзитивного
локально без 3-лап графа с несвязными окрестностями вершин.
Этот граф является локально 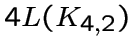 -графом,
то есть графом, любая окрестность вершины которого является
объединением четырех решетчатых
-графом,
то есть графом, любая окрестность вершины которого является
объединением четырех решетчатых ![]() -графов. Он
получается из наименьшего орбитала группы Хигмена-Симса при
представлении ее как транзитивной группы подстановок, действующей на классе
центральных инволюций.
-графов. Он
получается из наименьшего орбитала группы Хигмена-Симса при
представлении ее как транзитивной группы подстановок, действующей на классе
центральных инволюций.
С другой стороны, интересен следующий, связанный с данным, вопрос.
А именно, какими свойствами должен обладать граф, чтобы множество
его ребер оказалось орбиталом для группы подстановок, действующей
транзитивно на его вершинах (граф, изоморфный такому графу,
мы назовем орбитальным)?
Этот вопрос тесно связан с вопросом изучения групп автоморфизмов графов.
В работах [14], [15] Х. Еномото получил
характеризацию графов Хэмминга как орбитальных графов
для транзитивных групп подстановок с определенными ограничениями
на их подстепени.
Первая теорема третьей главы диссертации, опубликованная в [54],
усиливает результат Х. Еномото.
Для ее формулировки нам понадобится определение отделимого графа.
Граф ![]() назовем отделимым, если для любой вершины
назовем отделимым, если для любой вершины ![]() из
из
![]() подграф
подграф 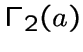 содержит вершины
содержит вершины ![]() на расстоянии 2 в
на расстоянии 2 в
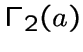 и
и ![]() -подграф
-подграф ![$[b]\cap [c]$](img101.gif) для любой такой пары
не пересекает
для любой такой пары
не пересекает ![]() .
.
Пусть ![]() -- связный вполне
регулярный граф
с параметрами
-- связный вполне
регулярный граф
с параметрами
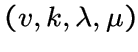 ,
, ![]() .
Граф
.
Граф ![]() отделим тогда и только тогда, когда
он является одним из следующих графов:
отделим тогда и только тогда, когда
он является одним из следующих графов:
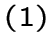 граф Хемминга
граф Хемминга 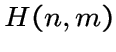 при
при
![]() ;
;
 треугольный граф
треугольный граф 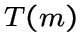 при
при ![]() ;
;
 граф Шлефли;
граф Шлефли;
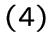 граф икосаэдра.
граф икосаэдра.
Используя классификацию реберно-регулярных
графов без 3-лап [29], М. Нумата в работе [30] получил
характеризацию
графов Грассмана и Джонсона как графов локально без 3-лап, в которых
все ![]() -подграфы являются изоморфными
реберно-регулярными графами
диаметра 2. Заметим, что если граф
-подграфы являются изоморфными
реберно-регулярными графами
диаметра 2. Заметим, что если граф ![]() удовлетворяет условию
теоремы М. Нуматы, то из последнего условия на все
удовлетворяет условию
теоремы М. Нуматы, то из последнего условия на все ![]() -подграфы
графа
-подграфы
графа ![]() непосредственно следует реберная регулярность самого
непосредственно следует реберная регулярность самого ![]() .
.
Наша следующая цель получить классификацию локально без 3-лап графов
с более слабым условием на ![]() -подграфы, которое не влечет
даже регулярности графа. Это стало возможно благодаря
классификации графов без 3-лап с равномощными
-подграфы, которое не влечет
даже регулярности графа. Это стало возможно благодаря
классификации графов без 3-лап с равномощными ![]() -подграфами.
С помощью этой классификации мы исследуем
класс графов, в которых окрестности вершин
не содержат 3-лап и все
-подграфами.
С помощью этой классификации мы исследуем
класс графов, в которых окрестности вершин
не содержат 3-лап и все ![]() -подграфы являются регулярными графами
валентности
-подграфы являются регулярными графами
валентности ![]() , где
, где ![]() .
В отличии от [30] мы не требуем даже равномощности всех
.
В отличии от [30] мы не требуем даже равномощности всех ![]() -подграфов.
Поскольку наше условие на
-подграфов.
Поскольку наше условие на ![]() -подграфы не влечет регулярности графа,
то мы дополнительно накладываем на граф условие редуцированности.
-подграфы не влечет регулярности графа,
то мы дополнительно накладываем на граф условие редуцированности.
Пусть ![]() -- связный граф, который
удовлетворяет следующим условиям:
-- связный граф, который
удовлетворяет следующим условиям:
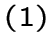 окрестность любой вершины из
окрестность любой вершины из ![]() не содержит
не содержит ![]() -лап;
-лап;

![]() содержит
содержит ![]() -лапу;
-лапу;
 все
все ![]() -подграфы из
-подграфы из ![]() являются регулярными
графами одинаковой валентности
являются регулярными
графами одинаковой валентности ![]() для некоторого числа
для некоторого числа ![]() ;
;
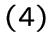 для любой вершины
для любой вершины ![]() множество
множество
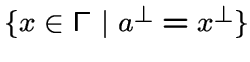 состоит из единственной вершины
состоит из единственной вершины ![]() .
.
Тогда ![]() является локально
является локально ![]() -графом, где
-графом, где
![]() один из следующих графов:
один из следующих графов:
![]()
![]() -расширение решетчатого
-расширение решетчатого ![]() -графа
при
-графа
при
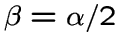 и
и ![]() ,
, ![]() ;
;
![]() треугольный граф
треугольный граф 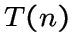 при
при ![]() ;
;
![]() граф Шлефли.
граф Шлефли.
Если граф ![]() является
является ![]() -расширением решетчатого
-расширением решетчатого ![]() -графа,
то класс локально
-графа,
то класс локально ![]() -графов довольно широк и труден
для изучения. Примерами таких графов являются графы Грассмана,
графы Джонсона и их частные.
-графов довольно широк и труден
для изучения. Примерами таких графов являются графы Грассмана,
графы Джонсона и их частные.
Пусть ![]() является
является ![]() -мерным векторным
пространством над конечным полем
-мерным векторным
пространством над конечным полем ![]() .
Графом Грассмана для
.
Графом Грассмана для ![]() -подпространств из
-подпространств из ![]() называется граф
называется граф
![$\left[V\atop m\right]$](img112.gif) с множеством вершин, равным
множеству всех подпространств размерности
с множеством вершин, равным
множеству всех подпространств размерности ![]() из
из ![]() , причем две вершины
, причем две вершины
![]() смежны тогда и только тогда, когда
смежны тогда и только тогда, когда
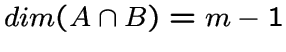 .
Если
.
Если ![]() -- конечное множество, то графом Джонсона для
-- конечное множество, то графом Джонсона для
![]() -подмножеств из
-подмножеств из ![]() называется граф с множеством вершин, равным
множеству
называется граф с множеством вершин, равным
множеству
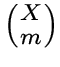 всех
всех ![]() -элементных подмножеств из
-элементных подмножеств из ![]() , причем две вершины
, причем две вершины ![]() смежны тогда и только тогда, когда
смежны тогда и только тогда, когда
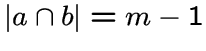 .
Если множество
.
Если множество ![]() состоит из
состоит из ![]() элементов, то такой граф
обозначим через
элементов, то такой граф
обозначим через 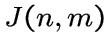 . Заметим, что граф
. Заметим, что граф 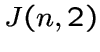 совпадает с
треугольным графом
совпадает с
треугольным графом 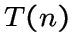 .
Пусть
.
Пусть ![]() -- некоторое разбиение множества вершин графа
-- некоторое разбиение множества вершин графа ![]() на подмножества. Частным
на подмножества. Частным
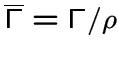 для графа
для графа ![]() по разбиению
по разбиению ![]() называется граф на фактор-множестве по
называется граф на фактор-множестве по ![]() множества вершин
множества вершин ![]() ,
в котором две вершины
,
в котором две вершины
![]() смежны только, если
смежны только, если
![]() и граф
и граф ![]() содержит ребро, которое соединяет
некоторую вершину из класса
содержит ребро, которое соединяет
некоторую вершину из класса ![]() с некоторой вершиной из класса
с некоторой вершиной из класса
![]() .
Пусть
.
Пусть ![]() и
и ![]() является разбиением множества вершин
графа Джонсона
является разбиением множества вершин
графа Джонсона 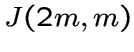 на двухэлементные классы, содержащие
на двухэлементные классы, содержащие
![]() -элементное подмножество и его дополнение в
-элементное подмножество и его дополнение в ![]() .
Частным графа Джонсона называется граф
.
Частным графа Джонсона называется граф 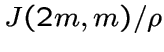 .
.
Графы Джонсона и частные графов Джонсона дают нам примеры локально
![]() -графов. Эти примеры не исчерпывают класс таких графов.
В статье [3] построены другие примеры локально
-графов. Эти примеры не исчерпывают класс таких графов.
В статье [3] построены другие примеры локально ![]() -графов
и найдены все локально
-графов
и найдены все локально ![]() -графы. Там же получено описание локально
-графы. Там же получено описание локально
![]() -графов, в которых
каждый
-графов, в которых
каждый ![]() -подграф является объединением изолированных четырехугольников.
Характеризация локально
-подграф является объединением изолированных четырехугольников.
Характеризация локально ![]() -графов при
-графов при ![]() получена Дж. Холлом в
[17]. Проблема полного описания локально
получена Дж. Холлом в
[17]. Проблема полного описания локально ![]() -графов
для любых
-графов
для любых ![]() остается открытой.
Мало пока известно в общем случае и о локально
треугольных графах.
остается открытой.
Мало пока известно в общем случае и о локально
треугольных графах.
Однако, если все ![]() -подграфы из
-подграфы из ![]() имеют диаметр 2, можно получить более точный ответ.
имеют диаметр 2, можно получить более точный ответ.
Пусть ![]() -- связный граф, который
удовлетворяет условиям теоремы и
все
-- связный граф, который
удовлетворяет условиям теоремы и
все ![]() -подграфы из
-подграфы из ![]() имеют диаметр 2.
Тогда
имеют диаметр 2.
Тогда ![]() является одним из следующих графов:
является одним из следующих графов:
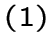 граф Грассмана;
граф Грассмана;
 граф Джонсона или его частное;
граф Джонсона или его частное;
 локально
локально 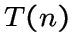 -граф при
-граф при ![]() ;
;
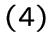 граф Госсета
граф Госсета 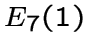 .
.
Все графы Грассмана, графы Джонсона и их частные, граф Госсета 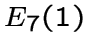 являются дистанционно-транзитивными графами.
являются дистанционно-транзитивными графами.
Заметим также, что граф системы корней ![]() (см. [5])
является локально
(см. [5])
является локально 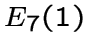 -графом и играет особую роль в теории графов,
у которых любое собственное значение не меньше, чем
-графом и играет особую роль в теории графов,
у которых любое собственное значение не меньше, чем ![]() .
По теореме А.Дж. Хоффмана [23] любой такой граф является либо
обобщенным реберным графом, либо подграфом
.
По теореме А.Дж. Хоффмана [23] любой такой граф является либо
обобщенным реберным графом, либо подграфом 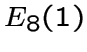 .
.
Заканчивается третья глава описанием сильно регулярных графов с
расщепляемыми окрестностями вершин.
Пусть ![]() -- некоторые множества. Скажем, что
-- некоторые множества. Скажем, что
![]() расщепляется
расщепляется ![]() и
и ![]() , если
, если ![]() содержится в
содержится в
![]() и пересечение
и пересечение ![]() пусто.
Э. Шульт в работе [33] классифицировал сильно регулярные
графы, в которых для любого ребра
пусто.
Э. Шульт в работе [33] классифицировал сильно регулярные
графы, в которых для любого ребра ![]() найдется такая
вершина
найдется такая
вершина ![]() из
из ![]() , что
, что ![]() расщепляется
расщепляется ![]() и
и ![]() .
Заметим, что в этом случае
.
Заметим, что в этом случае
![$[a]'\cap [b]=[a]'\cap [c]'$](img148.gif) и
и
![$[a]'\cap [c]=[a]'\cap [b]'$](img149.gif) .
В частности, антиокрестность
.
В частности, антиокрестность ![]() расщепляется
антиокрестностями вершин
расщепляется
антиокрестностями вершин ![]() и
и ![]() . В следующей теореме [52] это
условие накладывается на окрестности вершин,
причем снято ограничение на расположение вершины
. В следующей теореме [52] это
условие накладывается на окрестности вершин,
причем снято ограничение на расположение вершины ![]() .
.
Пусть ![]() -- сильно регулярный граф, в котором для
любого ребра
-- сильно регулярный граф, в котором для
любого ребра ![]() найдется такая вершина
найдется такая вершина ![]() , что
, что ![]() расщепляется
расщепляется ![]() и
и ![]() . Тогда граф
. Тогда граф ![]() изоморфен одному из
следующих графов:
изоморфен одному из
следующих графов:
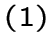 объединение
объединение ![]() полных подграфов при
полных подграфов при ![]() ;
;
 решетчатый
решетчатый ![]() -граф при
-граф при ![]() ;
;
 пятиугольник;
пятиугольник;
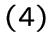 сильно регулярный граф с параметрами
сильно регулярный граф с параметрами 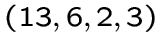 ;
;
 граф Шрикханде.
граф Шрикханде.
В последней главе диссертации изучаются некоторых теоретико-графовые свойства графов без 3-лап и их обобщений. В ней рассматривается, в частности, соотношение нижних параметров доминирования и неприводимости для графов без 3-лап и графов, все блоки которых не содержат 3-лап.
Некоторое множество ![]() вершин из графа
вершин из графа ![]() называется
доминирующим, если любая вершина, не принадлежащая
называется
доминирующим, если любая вершина, не принадлежащая ![]() ,
смежна не менее чем с одной вершиной из
,
смежна не менее чем с одной вершиной из ![]() .
Минимальное число элементов в доминирующем множестве вершин графа
.
Минимальное число элементов в доминирующем множестве вершин графа
![]() обозначается через
обозначается через
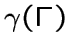 и называется нижним
параметром доминирования графа
и называется нижним
параметром доминирования графа ![]() .
Множество всех вершин из графа
.
Множество всех вершин из графа ![]() , смежных с вершиной
, смежных с вершиной ![]() , вместе
с
, вместе
с 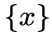 называется замкнутой окрестностью вершины
называется замкнутой окрестностью вершины ![]() .
Вершина
.
Вершина ![]() из
из ![]() неприводима относительно
неприводима относительно ![]() в
в ![]() , если ее
замкнутая окрестность содержит хотя бы одну вершину, не смежную ни с какой
другой вершиной
из
, если ее
замкнутая окрестность содержит хотя бы одну вершину, не смежную ни с какой
другой вершиной
из ![]() . Множество вершин
. Множество вершин ![]() называется неприводимым в
называется неприводимым в ![]() , если
все его вершины неприводимы относительно
, если
все его вершины неприводимы относительно ![]() в
в ![]() .
Заметим, что если
.
Заметим, что если ![]() -- минимальное доминирующее множество некоторого
графа
-- минимальное доминирующее множество некоторого
графа ![]() , то оно неприводимо в
, то оно неприводимо в ![]() .
Более того, множество
.
Более того, множество ![]() является
максимальным (относительно включения) неприводимым множеством графа
является
максимальным (относительно включения) неприводимым множеством графа ![]() .
Этот факт послужил основой для введения и изучения понятия неприводимости.
Среди всех максимальных неприводимых множеств выберем множество
.
Этот факт послужил основой для введения и изучения понятия неприводимости.
Среди всех максимальных неприводимых множеств выберем множество ![]() ,
содержащее наименьшее число вершин. Число вершин в
,
содержащее наименьшее число вершин. Число вершин в ![]() назовем нижним параметром неприводимости для графа
назовем нижним параметром неприводимости для графа ![]() и обозначим через
и обозначим через
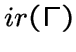 .
.
Поскольку каждое минимальное доминирующее множество является
максимальным неприводимым, то
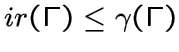 для любого графа
для любого графа ![]() .
Неравенство
.
Неравенство
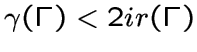 было получено независимо
в [1] и [4]. Изучению параметров
доминирования и неприводимости в разных классах графов было посвящено
несколько работ (см., например, [1], [4], [12], [16],
[39]). В [12] П. Дамашке получил оценку
было получено независимо
в [1] и [4]. Изучению параметров
доминирования и неприводимости в разных классах графов было посвящено
несколько работ (см., например, [1], [4], [12], [16],
[39]). В [12] П. Дамашке получил оценку
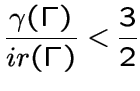 для случая, когда
граф
для случая, когда
граф ![]() является деревом.
Этот результат был расширен Л. Фолькманом в [39]. Он доказал неравенство
является деревом.
Этот результат был расширен Л. Фолькманом в [39]. Он доказал неравенство
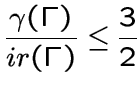 в случае,
когда
в случае,
когда ![]() является блок-графом и в случае, когда граф
является блок-графом и в случае, когда граф ![]() содержит
не более двух циклов.
содержит
не более двух циклов.
Так как по определению любой блок в блок-графе является кликой, то точки сочленения внутри любого блока смежны между собой. Граф, обладающий таким свойством, назовем кликово-сочлененным графом.
В работе [41] показано, что оценка
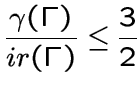 справедлива
для класса графов без 3-лап. Там же приводится
серия примеров, которая показывает точность этой границы даже в классе
раздуваний графов.
Продолжая это исследование, мы изучаем нижние параметры
доминирования и неприводимости в кликово-сочлененных графах, все блоки
которых являются графами без 3-лап.
В частности, покажем, что для них справедливо неравенство
справедлива
для класса графов без 3-лап. Там же приводится
серия примеров, которая показывает точность этой границы даже в классе
раздуваний графов.
Продолжая это исследование, мы изучаем нижние параметры
доминирования и неприводимости в кликово-сочлененных графах, все блоки
которых являются графами без 3-лап.
В частности, покажем, что для них справедливо неравенство
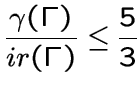 .
Более точно мы доказываем следующие два утверждения [48].
.
Более точно мы доказываем следующие два утверждения [48].
Пусть ![]() -- связный
кликово-сочлененный граф и
-- связный
кликово-сочлененный граф и ![]() -- максимальное неприводимое подмножество
вершин из
-- максимальное неприводимое подмножество
вершин из ![]() .
.
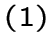 Если все блоки графа
Если все блоки графа ![]() не содержат 3-лап, то существует
доминирующее множество
не содержат 3-лап, то существует
доминирующее множество ![]() для
для ![]() такое, что выполнено неравенство
такое, что выполнено неравенство
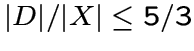 .
.
 Если все блоки графа
Если все блоки графа ![]() являются реберными графами
графов без треугольников, то существует доминирующее множество
являются реберными графами
графов без треугольников, то существует доминирующее множество ![]() для
для
![]() такое, что выполнено неравенство
такое, что выполнено неравенство
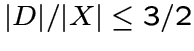 .
.
Автор глубоко признателен профессору А.А. Махневу за дружеское участие, постоянное внимание и помощь в работе.