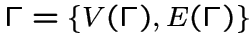 -- конечный обыкновенный граф
с множеством вершин
-- конечный обыкновенный граф
с множеством вершин 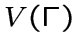 и множеством ребер
и множеством ребер 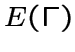 .
.
Пусть
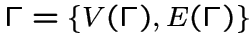 -- конечный обыкновенный граф
с множеством вершин
-- конечный обыкновенный граф
с множеством вершин 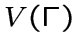 и множеством ребер
и множеством ребер 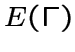 .
.
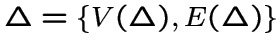 такой, что его множество вершин
такой, что его множество вершин
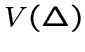 является подмножеством множества вершин из
является подмножеством множества вершин из 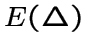 является подмножеством множества ребер
из
является подмножеством множества ребер
из
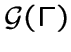 .
.
Поскольку в диссертации не рассматриваются подграфы, которые не являются порожденными, то подграфом называется только порожденный подграф.
Сокращяя обозначения, используем для множества вершин
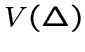 и для подграфа
и для подграфа ![]() один и тот же символ
один и тот же символ ![]() .
.
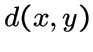 -- расстояние между вершинами
-- расстояние между вершинами 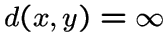 , если вершины
, если вершины
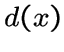 вершины
вершины 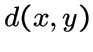 , где
, где
К названиям понятий, соответствующих дополнительному графу, добавляют приставку "ко".
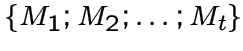 .
.
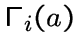 обозначается
подграф на множестве всех вершин, которые находятся на расстоянии
обозначается
подграф на множестве всех вершин, которые находятся на расстоянии 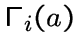 называется
называется
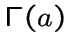 обозначается
обозначается 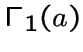 .
Если граф
.
Если граф 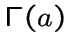 обозначается через
обозначается через
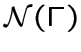 .
.
![$[a]\cup \{a\}$](img201.gif) обозначим через
обозначим через
![$[a]_\Delta$](img202.gif) окрестность
окрестность ![$[a]_\Delta$](img202.gif) обозначим пересечение окрестности
обозначим пересечение окрестности
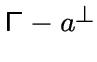 обозначается через
обозначается через
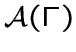 .
.
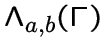 или просто
или просто
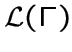 .
.
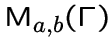 или просто
или просто
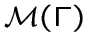 .
.
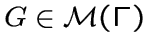 подграф
подграф
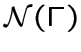 содержит
содержит
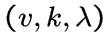 , если
, если 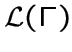 имеет
имеет
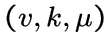 , если
, если
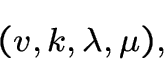
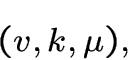
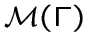 имеет
имеет
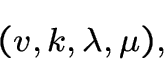
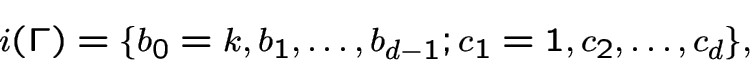
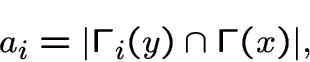
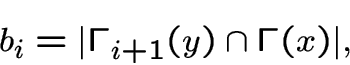
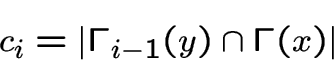
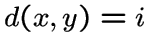 .
.
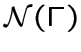 изоморфен некоторому графу из
изоморфен некоторому графу из
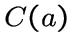 , содержащий не менее одной вершины, причем вершины
из различных клик
, содержащий не менее одной вершины, причем вершины
из различных клик 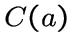 и
и 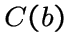 смежны тогда и только тогда,
когда вершины
смежны тогда и только тогда,
когда вершины
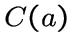 содержит
содержит
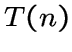 называется реберный граф
полного графа с
называется реберный граф
полного графа с
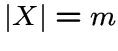 ,
, 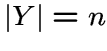 , а пары
, а пары 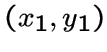 и
и 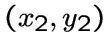 смежны тогда
и только тогда, когда
смежны тогда
и только тогда, когда
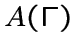 графа
графа 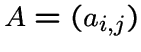 , строки и колонки которой занумерованы
вершинами графа
, строки и колонки которой занумерованы
вершинами графа
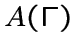 .
.
Известно, что наименьшее собственное значение треугольных и решетчатых
графов равно ![]() .
.
Отметим некоторые свойства треугольных и решетчатых графов, которые нам необходимы.
Пусть ![]() является
является ![]() графом. Перенумеруем
вершины первой доли числами от
графом. Перенумеруем
вершины первой доли числами от ![]() до
до ![]() , а вершины второй доли
числами от
, а вершины второй доли
числами от ![]() до
до ![]() .
Множество всех вершин решетчатого
.
Множество всех вершин решетчатого ![]() -графа
-графа ![]() , который
является реберным графом графа
, который
является реберным графом графа ![]() , можно разложить
в объединение
, можно разложить
в объединение ![]() максимальных непересекающихся клик
максимальных непересекающихся клик
![]() по
по ![]() вершин каждая. Клика
вершин каждая. Клика ![]() соответствует
множеству ребер, исходящих из вершины с номером
соответствует
множеству ребер, исходящих из вершины с номером ![]() первой доли графа
первой доли графа
![]() . Аналогично, множество
всех вершин решетчатого графа можно разложить
и в объединение
. Аналогично, множество
всех вершин решетчатого графа можно разложить
и в объединение ![]() максимальных непересекающихся клик
максимальных непересекающихся клик
![]() по
по
![]() вершин каждая. Клика
вершин каждая. Клика ![]() соответствует множеству ребер,
исходящих из вершины с номером
соответствует множеству ребер,
исходящих из вершины с номером ![]() второй доли графа
второй доли графа ![]() .
Легко видеть, что
.
Легко видеть, что
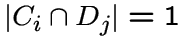 для всех
для всех
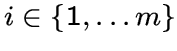 ,
,
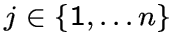 , поскольку
, поскольку ![]() соответствует единственному ребру соединяющему вершину
соответствует единственному ребру соединяющему вершину ![]() первой доли
графа
первой доли
графа ![]() с вершиной
с вершиной ![]() второй доли графа
второй доли графа ![]() .
.
Таким образом, окрестность каждой вершины в решетчатом ![]() -графе
является объединением двух изолированных клик на
-графе
является объединением двух изолированных клик на ![]() и
и ![]() вершинах
соответственно, то есть она изоморфна
вершинах
соответственно, то есть она изоморфна
![]() .
.
В любом решетчатом ![]() -графе
-графе ![]() все его подграфы из
все его подграфы из
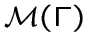 являются
являются ![]() -кокликами, а все его подграфы из
-кокликами, а все его подграфы из
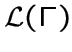 являются
являются 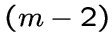 -кликами или
-кликами или 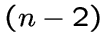 -кликами.
-кликами.
Треугольный граф 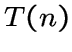 является локально решетчатым
является локально решетчатым 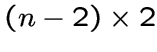 графом.
графом.
В любом треугольном графе 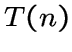 все его подграфы
все его подграфы
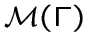 изоморфны
изоморфны ![]() , то есть являются четырехугольниками, а все его подграфы
из
, то есть являются четырехугольниками, а все его подграфы
из
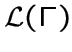 изоморфны
изоморфны ![]() .
.
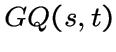 называется конечная
геометрия с множествами точек и прямых
называется конечная
геометрия с множествами точек и прямых 1. Две точки инцидентны не более одной прямой.
2. Две прямые инцидентны не более одной точке. Если две прямые инцидентны одной точке, то говорят, что эти прямые пересекаются.
3. Для любой прямой ![]() и для любой не лежащей на ней точки
и для любой не лежащей на ней точки
![]() существует только одна прямая
существует только одна прямая 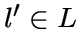 , инцидентная
, инцидентная ![]() и
пересекающая прямую
и
пересекающая прямую ![]() .
.
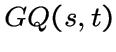 называется граф, множеством вершин которого является множество точек
называется граф, множеством вершин которого является множество точек
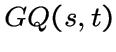 , и две вершины смежны тогда и только тогда, когда точки
лежат на одной прямой.
, и две вершины смежны тогда и только тогда, когда точки
лежат на одной прямой.
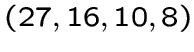 , который является дополнительным к графу инцидентностей
обобщенного четырехугольника
, который является дополнительным к графу инцидентностей
обобщенного четырехугольника 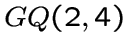 .
.
Известно, что граф инцидентностей обобщенного четырехугольника
является сильно регуляреным графом.
Обобщенный четырехугольник 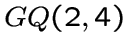 существует и притом только один
(см. теорему 1.15.2 и пример (iii) на стр. 30 монографии [6]).
существует и притом только один
(см. теорему 1.15.2 и пример (iii) на стр. 30 монографии [6]).
Заметим, что если ![]() граф Шлефли, то он является локально
граф Шлефли, то он является локально
![]() -графом, где
-графом, где ![]() -- граф Клебша. Более того, поскольку
в
-- граф Клебша. Более того, поскольку
в 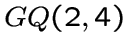 через любую точку
через любую точку ![]() проходит 5 прямых, на каждой из
которых по две точки, отличные от точки
проходит 5 прямых, на каждой из
которых по две точки, отличные от точки ![]() , то любая антиокрестность
в графе Шлефли изоморфна графу
, то любая антиокрестность
в графе Шлефли изоморфна графу ![]() . Таким образом
любой подграф из
. Таким образом
любой подграф из
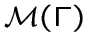 изоморфен
изоморфен ![]() .
.
В следующем пункте приводится другое определение графа Шлефли.
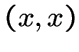 является четным числом для всех
является четным числом для всех
Подмножество векторов
данной корневой решетки ![]() образуют систему корней
образуют систему корней ![]() в
в
![]() , то есть
, то есть ![]() является конечным множеством ненулевых
векторов, порождающих
является конечным множеством ненулевых
векторов, порождающих ![]() , таких, что выполнены следующие три условия:
, таких, что выполнены следующие три условия:
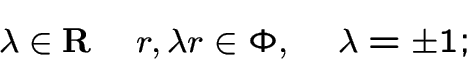
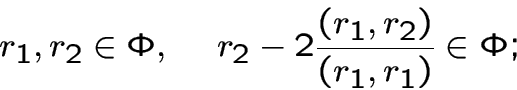
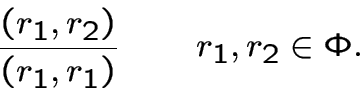
Векторы системы корней ![]() называются корневыми векторами или
корнями.
Систематическое изложение теории корневых систем можно найти в книге Бурбаки
[5]. Нам понадобится определение системы корней
называются корневыми векторами или
корнями.
Систематическое изложение теории корневых систем можно найти в книге Бурбаки
[5]. Нам понадобится определение системы корней ![]() и
соответствующего ей графа.
и
соответствующего ей графа.
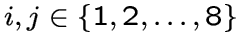
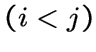 и вектором
и вектором
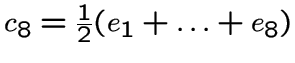 .
.
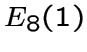 . Этот
граф имеет 240 вершин. Причем 112 вершин вида
. Этот
граф имеет 240 вершин. Причем 112 вершин вида
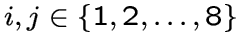
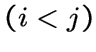 и
128 вершин вида
и
128 вершин вида
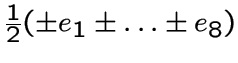 , где число
минусов четно.
, где число
минусов четно.
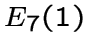 является подграфом графа
является подграфом графа 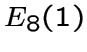 и
имеет 56 вершин вида
и
имеет 56 вершин вида 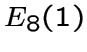 .
.
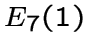 является графом Тэйлора.
Окрестность каждой вершины в
является графом Тэйлора.
Окрестность каждой вершины в 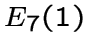 -- граф Шлефли.
-- граф Шлефли.
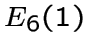 является подграфом графа
является подграфом графа 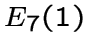 и
имеет 27 вершин вида
и
имеет 27 вершин вида 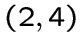 .
.
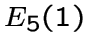 является подграфом графа
является подграфом графа 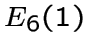 и
имеет 16 вершин вида
и
имеет 16 вершин вида 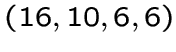 . Окрестность каждой вершины в
. Окрестность каждой вершины в 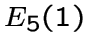 изоморфна
треугольному графу
изоморфна
треугольному графу  . Заметим, что граф
. Заметим, что граф  является
дополнительным к графу Петерсена (см. рис.
является
дополнительным к графу Петерсена (см. рис. ![[*]](crossref.gif) ).
).
Пусть ![]() некоторый граф и
некоторый граф и ![]() некоторый класс графов.
некоторый класс графов.
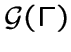 , изоморфного
, изоморфного
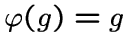 для любой вершины
для любой вершины
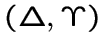 -однородным типа
-однородным типа
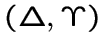 -однородным,
если для любого подграфа
-однородным,
если для любого подграфа
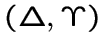 -регулярным типа
-регулярным типа
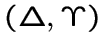 -регулярным,
если для подграфа
-регулярным,
если для подграфа
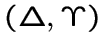 -регулярным графом для любого
-регулярным графом для любого
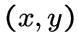 зависит только от того, является
зависит только от того, является
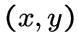 ребром или нет.
ребром или нет.
Следующие примеры дистанционно-регулярных графов играют важную роль в данной работе.
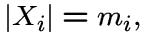 а пары
а пары
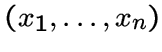 и
и
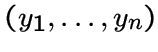 смежны тогда и только тогда, когда существует
единственное
смежны тогда и только тогда, когда существует
единственное
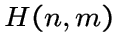 или
или
Пусть ![]() является
является ![]() -мерным векторным
пространством над конечным полем
-мерным векторным
пространством над конечным полем ![]() .
.
![$\left[V\atop m\right]$](img112.gif) с множеством вершин, равным
множеству всех подпространств размерности
с множеством вершин, равным
множеству всех подпространств размерности 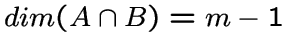 .
.
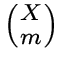 всех
всех 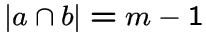 .
Если множество
.
Если множество 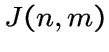 . Заметим, что граф
. Заметим, что граф 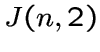 совпадает с
треугольным графом
совпадает с
треугольным графом 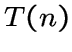 .
.
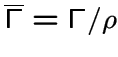 для графа
для графа
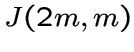 на двухэлементные классы, содержащие
на двухэлементные классы, содержащие
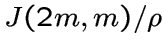 .
.
![[*]](crossref.gif) ).
).
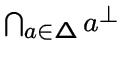 .
.
 .
.
 .
Понятно, этот подграф совпадает с
.
Понятно, этот подграф совпадает с 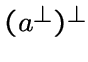 .
.
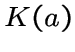 обозначается через
обозначается через
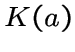 состоит
из единственной вершины
состоит
из единственной вершины
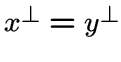 .
Редукцией графа
.
Редукцией графа
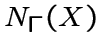 обозначим множество
обозначим множество
![$\ds\bigcup_{x\in X} [x]$](img343.gif) , то есть
множество вершин, которые смежны хотя бы с одной вершиной из
, то есть
множество вершин, которые смежны хотя бы с одной вершиной из ![$\ds N_\Gamma[X]$](img344.gif) обозначим множество
обозначим множество
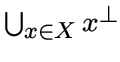 .
Если граф
.
Если граф 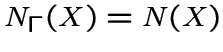 и
и
![$N_\Gamma[X]=N[X]$](img347.gif) .
Заметим, что если
.
Заметим, что если ![$N(X)=
[x]$](img348.gif) и
и ![$N[X]=x^\bot$](img349.gif) .
.
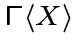 . Если граф
. Если граф 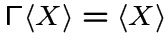 .
.
![$N_\Gamma[X] =V(\Gamma)$](img352.gif) .
.
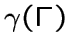 и называется нижним
параметром доминирования графа
и называется нижним
параметром доминирования графа
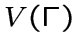 ,
то множество
,
то множество
![$PN(x) =x^\bot\setminus N[X\setminus \{x\}]$](img353.gif) называется
называется
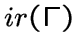 .
.
Вершина ![]() связного графа
связного графа ![]() называется точкой сочленения, если
если
называется точкой сочленения, если
если ![]() является несвязным графом.
является несвязным графом.
Связный граф называется блоком, если он не имеет точек сочленения.
Блоком графа ![]() называется связный подграф
называется связный подграф ![]() ,
который не имеет точек сочленения и максимален относительно свойства
"не иметь точек сочленения". Если блок не является ребром, то это
максимальный 2-связный подграф графа
,
который не имеет точек сочленения и максимален относительно свойства
"не иметь точек сочленения". Если блок не является ребром, то это
максимальный 2-связный подграф графа ![]() .
.
Блок-граф -- это граф, в котором все блоки являются кликами.
Через
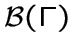 обозначим множество всех блоков графа
обозначим множество всех блоков графа
![]() , а через
, а через
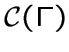 -- множество всех точек сочленения для
-- множество всех точек сочленения для
![]() .
.
Граф ![]() называется кликово-сочлененным,
если множество вершин из
называется кликово-сочлененным,
если множество вершин из
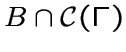 образуют клику для каждого блока
образуют клику для каждого блока ![]() из
из 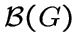 .
.
Заметим, что любой блок-граф является кликово сочлененным графом.