

Актуальность темы.В настоящее время в исследования графов с условиями симметрии вовлекаются симметрии все более общего вида. Сначала это были условия дистанционной транзитивности и дистанционной регулярности графов, а затем и более общие условия комбинаторной симметричности. Оказалось, что в некоторых случаях комбинаторная симметрия графа влечет его дистанционную транзитивность. В настоящей диссертационной работе развиваются новые методы исследования некоторых условий комбинаторной симметрии, которые дают возможность в ряде случаев получить полную классификацию рассматриваемых объектов.
Первые результаты о графах с условиями комбинаторной симметрии
были получены в пятидесятых годах. Пусть 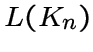 -- реберный граф полного графа
-- реберный граф полного графа ![]() или в других обозначениях треугольный граф
или в других обозначениях треугольный граф 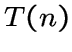 .
Этот граф является сильно регулярным графом с параметрами
.
Этот граф является сильно регулярным графом с параметрами
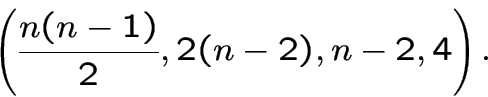
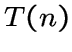 определяется однозначно своими параметрами для всех
определяется однозначно своими параметрами для всех 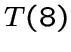 , такие же параметры имеют только три графа, которые были
найдены Л.С. Чангом в 1949 году [10].
, такие же параметры имеют только три графа, которые были
найдены Л.С. Чангом в 1949 году [10].
Реберный граф 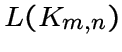 полного
многодольного графа
полного
многодольного графа ![]() (решетчатый
(решетчатый ![]() -граф)
является кореберно-регулярным
графом с параметрами
-граф)
является кореберно-регулярным
графом с параметрами
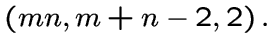 При
При ![]() решетчатый граф является сильно регулярным
графом с параметрами
решетчатый граф является сильно регулярным
графом с параметрами
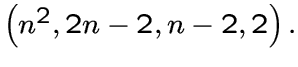 С.С. Шрикханде в [35] показал, что при
С.С. Шрикханде в [35] показал, что при ![]() граф
граф 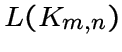 определяется этими параметрами, а при
определяется этими параметрами, а при ![]() ,
кроме
,
кроме 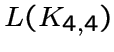 , существует еще в точности один граф, который теперь
называется графом Шрикханде.
Ситуацию без предположения о равенстве параметров
, существует еще в точности один граф, который теперь
называется графом Шрикханде.
Ситуацию без предположения о равенстве параметров ![]() и
и ![]() рассмотрели
независимо Дж.В. Мун [31] и А.Дж. Хоффман [22].
рассмотрели
независимо Дж.В. Мун [31] и А.Дж. Хоффман [22].
Матрица смежности графа ![]() -- это матрица
-- это матрица
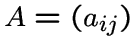 , строки и столбцы которой перенумерованы вершинами графа
, строки и столбцы которой перенумерованы вершинами графа
![]() , причем
, причем ![]() , если
, если ![]() является ребром в
является ребром в ![]() ,
,
![]() в противном случае.
Матрица смежности сильно регулярного графа
в противном случае.
Матрица смежности сильно регулярного графа ![]() с параметрами
с параметрами
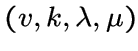 кроме собственного значения, равного
кроме собственного значения, равного ![]() , имеет
еще два действительных собственных значения разных знаков.
Если у сильно регулярного графа
, имеет
еще два действительных собственных значения разных знаков.
Если у сильно регулярного графа ![]() набор параметров
набор параметров
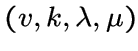 такой же,
как у треугольных или решетчатых
такой же,
как у треугольных или решетчатых ![]() -графов, то
отрицательное собственное значение его матрицы смежности равно
-графов, то
отрицательное собственное значение его матрицы смежности равно ![]() .
Более того, из теории действительных симметрических матриц
следует, что в этом случае любой порожденный подграф графа
.
Более того, из теории действительных симметрических матриц
следует, что в этом случае любой порожденный подграф графа ![]() не может иметь собственных значений, меньших
не может иметь собственных значений, меньших ![]() .
Это свойство дает возможность восстановить строение графа
.
Это свойство дает возможность восстановить строение графа ![]() с набором параметров, как у треугольных или решетчатых
с набором параметров, как у треугольных или решетчатых ![]() -графов.
-графов.
Граф ![]() называется сильным, если для любой пары
называется сильным, если для любой пары ![]() его вершин
число общих смежных с ними вершин зависит только от того, является
его вершин
число общих смежных с ними вершин зависит только от того, является ![]() ребром или нет.
Результаты Л.С. Чанга, С.С. Шрикханде и А.Дж. Хоффмана
были объединены Дж.Дж. Зейделем [34], который определил все сильные
графы с наименьшим собственным значением
ребром или нет.
Результаты Л.С. Чанга, С.С. Шрикханде и А.Дж. Хоффмана
были объединены Дж.Дж. Зейделем [34], который определил все сильные
графы с наименьшим собственным значением ![]() . Дж.Дж. Зейдель
показал, что кроме треугольных графов
. Дж.Дж. Зейдель
показал, что кроме треугольных графов 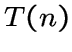 и решетчатых
и решетчатых ![]() -графов,
сильными графами, которые имеют наименьшее собственное значение
-графов,
сильными графами, которые имеют наименьшее собственное значение
![]() , являются только графы
, являются только графы ![]() , три графа Чанга,
графы Шрикханде, Шлефли, Клебша и Петерсена.
, три графа Чанга,
графы Шрикханде, Шлефли, Клебша и Петерсена.
Применяя метод С.С. Симса [36] перечисления 4-вершинных подграфов,
М.Д. Хестенс и Д.Г. Хигман в работе [19] показали,
что в сильно регулярных графах число 4-вершинных подграфов любого
заданного вида определяет число 4-вершинных подграфов всех других видов.
Это свойство позволило М.Д. Хестенсу и
Д.Г. Хигману получить более экономное доказательство теоремы
Дж.Дж. Зейделя для случая сильно регулярных графов.
Среди возможных 4-вершинных подграфов наиболее важную роль играют
подграфы, изоморфные ![]() (полный 4-вершинный граф),
(полный 4-вершинный граф), ![]() (полный 4-вершинный граф с удаленным ребром) и
(полный 4-вершинный граф с удаленным ребром) и ![]() (полный двудольный граф с долями из одной и трех вершин).
(полный двудольный граф с долями из одной и трех вершин).
Заметим, что если граф ![]() с наименьшим собственным значением, равным
с наименьшим собственным значением, равным
![]() , содержит 3-лапу
, содержит 3-лапу
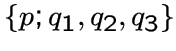 (4-вершинный подграф, изоморфный
(4-вершинный подграф, изоморфный ![]() ),
то любая вершина
),
то любая вершина
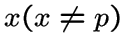 из
из ![]() , смежная с вершинами
, смежная с вершинами ![]() и
и ![]() , смежна с
, смежна с ![]() и не смежна с
и не смежна с ![]() . В противном случае подграф на
. В противном случае подграф на
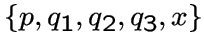 имеет собственное значение, которое строго меньше
имеет собственное значение, которое строго меньше ![]() .
Как уже было отмечено, это невозможно.
Таким образом, граф с наименьшим собственным значением, равным
.
Как уже было отмечено, это невозможно.
Таким образом, граф с наименьшим собственным значением, равным
![]() , либо не содержит 3-лап, либо содержит 3-лапы, но тогда окрестность
любой его вершины не содержит 3-лап.
, либо не содержит 3-лап, либо содержит 3-лапы, но тогда окрестность
любой его вершины не содержит 3-лап.
Цель работы.Исследование класса графов без 3-лап и локально без 3-лап в совокупности с некоторыми условиями комбинаторной симметрии, в том числе и с некоторыми условиями регулярности.
Общая методика исследований.В диссертационной работе развиваются новые методы локального анализа комбинаторно-симметричных графов.
Научная новизна.Все результаты диссертации являются новыми.
Практическая ценность.Диссертация носит теоретический характер. Результаты и методы работы могут быть использованы в алгебраической комбинаторике, теории графов и теории конечных групп.
Апробация работы.Результаты работы докладывались на Международных конференциях по алгебре в 1993 году в Красноярске [42], в 1996 году в Санкт-Петербурге [51] и в 1998 году в Москве [46], на III Краковской международной конференции по теории графов в 1997 году [50], на Пятом чехо-словацком симпозиуме по комбинаторике, теории графов, алгоритмам и приложениям в 1998 году [47], на конференции "Случайные структуры и алгоритмы" в Познани в 1999 году, на международной конференции памяти П. Эрдеша в Будапеште в 1999 году [48], на семинаре кафедры высшей алгебры Московского государственного университета, на семинаре "Экстремальные задачи теории графов" в Институте математики СО РАН, на семинаре отдела алгебры и топологии Института математики и механики УрО РАН, на городском алгебраическом семинаре в Уральском государственном университете.
Публикации.Основные результаты диссертации опубликованы в работах [41]-[55]. Работы [49]-[55] написаны в нераздельном соавторстве с А.А. Махневым. Из работы [41] в диссертации использованы только результаты, принадлежащие автору.
Объем и структура работы.Диссертационная работа состоит из введения, четырех глав и списка литературы (72 наименования), занимает 195 страниц текста, набранного в пакете LATEX. Нумерация основных теорем во введении одинарная, теорем и лемм в главах тройная (номер главы, номер параграфа, номер утверждения).