Для составления уравнений Лагранжа второго рода, описывающих движение МТМ, необходимо вычислить кинетическую энергию МТМ. Она складывается из кинетической энергии носителя и кинетической энергии звеньев. По формуле Кенига кинетическая энергия
Для составления уравнений Лагранжа второго рода, описывающих движение МТМ, необходимо
вычислить кинетическую энергию МТМ. Она складывается из кинетической энергии носителя и
кинетической энергии звеньев. По формуле Кенига кинетическая энергия ![]() -го звена,
-го звена,
![]() , равна величине
, равна величине
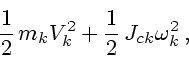
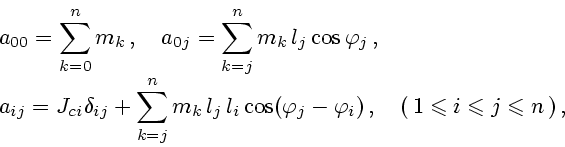
Далее приступим к вычислению обобщенных сил. Понадобятся обозначения: ![]() -
вектор скорости центра масс
-
вектор скорости центра масс ![]() -го звена МТМ,
-го звена МТМ, ![]() - величина этой скорости. Согласно
лемме 1.1 справедливы формулы
- величина этой скорости. Согласно
лемме 1.1 справедливы формулы
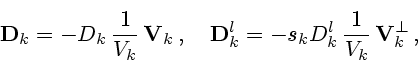
Пусть
![]() - матрица-столбец
обобщенных сил, соответствующих обобщенным координатам
- матрица-столбец
обобщенных сил, соответствующих обобщенным координатам ![]() ,
,
![]() ,
,
![]() . Используя выписанные выше формулы для составляющих гидродинамических сил,
можно получить выражение:
. Используя выписанные выше формулы для составляющих гидродинамических сил,
можно получить выражение:
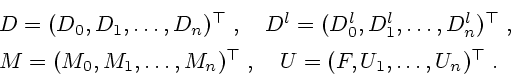
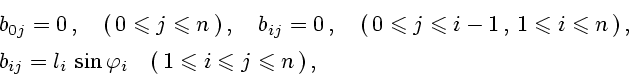
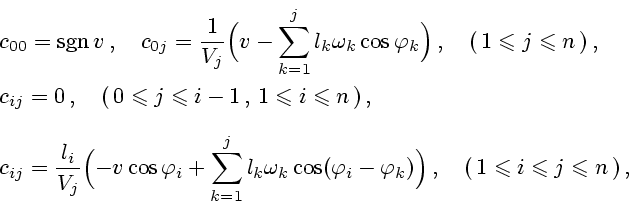
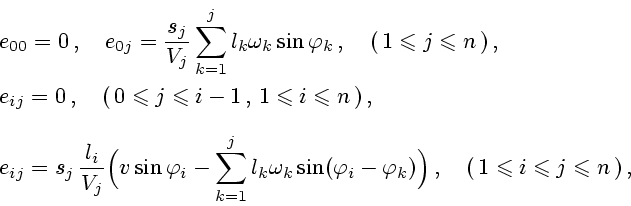
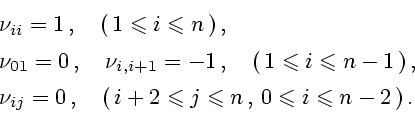
Приведенной информации достаточно, чтобы получить уравнения движения МТМ в виде
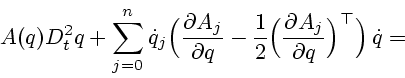
Выражение для мощности управляющих сил и моментов имеет вид
Затруднение, связанное с перемножением в (7.2) импульсных воздействий на одновременно претерпевающие скачки обобщенные скорости было преодолено в рамках физического анализа совершаемой работы. Однако существует и возможность придания выражению (7.2) строгого смысла.
Теорема 7.1. Работа действующих на МТМ управлений допускает представление
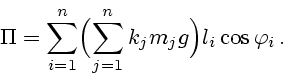
Действительно, чтобы обосновать данное утверждение следует разрешить уравнения
Лагранжа (7.1) относительно управляющих воздействий и подставить результат в (7.2). Затем
в полученном соотношении
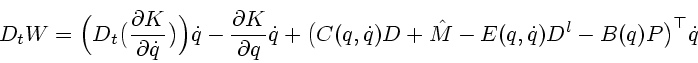
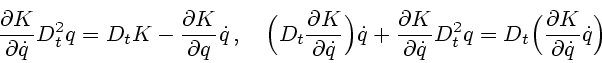
В заключение обсудим технический смысл исследованных выше задач динамической оптимизации.
Участок фазовой траектории тела, на котором мощность каждого из управляющих воздействий
неотрицательна, естественно назвать разгонным. Задачи, рассмотренные в этой работе, с
содержательной точки зрения состоят в минимизации разности энергетических в техническом
смысле затрат на разгон и торможение при заданных расстоянии и времени перемещения.
Отсюда если интервал ![]() процесса оптимального управления является разгонным, то
можно говорить о решении задачи заданного перемещения тела с минимальными энергетическими
в техническом смысле затратами. Очевидно, гипотеза 1 о квазистационарности оптимального
обтекания гарантирует этот факт.
процесса оптимального управления является разгонным, то
можно говорить о решении задачи заданного перемещения тела с минимальными энергетическими
в техническом смысле затратами. Очевидно, гипотеза 1 о квазистационарности оптимального
обтекания гарантирует этот факт.
Поступила 15.11.99