| (8.1) |
If we consider the one-dimensional discretized Schrodinger equation
In order to scale the spectrum, the irrational number ![]() is
replaced by a sequence of rational numbers which are obtained by
truncating the continued fraction expansion of
is
replaced by a sequence of rational numbers which are obtained by
truncating the continued fraction expansion of ![]() For
example,
For
example, ![]() is approximated by a sequence of rational
numbers
is approximated by a sequence of rational
numbers
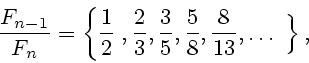
For the Fibonacci model, ![]() takes only two values:
takes only two values: ![]() and
and ![]() (the potential is constant, except for discontinuities) and the
spectrum is purely singular continuous (critical wave functions).
(the potential is constant, except for discontinuities) and the
spectrum is purely singular continuous (critical wave functions).
Instead, when the potential ![]() is a smooth function, the spectrum
is purely absolutely continuous (extended wave functions) for
small
is a smooth function, the spectrum
is purely absolutely continuous (extended wave functions) for
small ![]() and a purely dense point (localized wave
functions) for large
and a purely dense point (localized wave
functions) for large ![]() . For an intermediate value of
. For an intermediate value of
![]() the spectrum is a mixture of absolutely continuous
parts and dense point parts, which are separated by a finite
number of mobility edges. There is no singular continuous part.
The exception is the Harper model, where there is a singular
continuous spectrum (critical states) at the critical point
the spectrum is a mixture of absolutely continuous
parts and dense point parts, which are separated by a finite
number of mobility edges. There is no singular continuous part.
The exception is the Harper model, where there is a singular
continuous spectrum (critical states) at the critical point
![]()
Hence, a singular continuous spectrum rarely appears for a
potential ![]() that is a smooth function of
that is a smooth function of ![]()