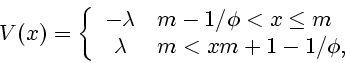7 Wave functions on a Fibonacci lattice

The properties of the wave functions for one-dimensional quasiperiodic discrete Schrodinger equations have been thoroughly studied by Kohmoto and others [13,14,15]. In quasiperiodic systems, the wave functions exhibit three possibilities:
1) localized wave functions (dense-point spectrum);
2) extended wave functions (absolutely continuous spectrum);
3) critical wave functions (singular continuous spectrum).

Wave functions of this last type are further classified into two types: selfsimilar and non-self-similar. It has been shown that a wave function which corresponds to a cycle of the renormalization group map is self-similar. On the other hand, a wave function which corresponds to a bounded chaotic orbit is not self-similar.

For several forms of the potential $V(x),$ the properties of the wave functions and the spectra have been thoroughly investigated [16,17]. The model defined by

$$V(x) = \lambda \cos (2\pi x),$$ (7.1)

which is known as the Harper model,¹ undergoes a metal-insulator transition at $\lambda = 2.$ That is, for $\lambda < 2,$ all the states are extended, while for $\lambda > 2,$ all the states are localized. At $\lambda = 2,$ all the states are critical.

In the model defined by

$$V(x) = \lambda \tan (2\pi x),$$ (7.2)

all the states are localized for any value of $\lambda.$

An important model is the Fibonacci model, defined by $\frac{{\sqrt 5-1}}{2}=\frac{1}{\phi}$ (the reciprocal value of the Golden Mean) and

$$V(x) = \left\{ \begin{array}{cl} -\lambda & m-1/\phi<x\le m \\ \lambda & m<xm+1-1/\phi, \\ \end{array} \right.$$

where $m$ is an integer. In this model, all the states are critical, irrespective of the value of $\lambda.$