9 Renormalization group of El Naschie

In the last decade, there has been a great interest in the application of fractal geometry to physics, for which integer and noninteger Hausdorff-fractal dimensions of a geometrical structure is one of the most important tools. El Naschie is a prolific physicist from the University of Cambridge, United Kingdom, who has introduced the notion of a 3 + 1-dimensional space-time, that he calls ``Cantorian space-time" [19].

The possibility that spatial chaos could model this real Cantorian space-time using fractal geometry has been investigated by El Naschie [20]. Based on a renormalization transformation, he derives an expectation value and the Hausdorff dimension of a basic set at criticality. For this, he needs four points (Cantorions) and a two-dimensional lattice rectangular block. Considering the position of these Cantorions, there are three different cases, where (a) two, (b) three, or (c) all the four intersection points of the block are occupied.

For case (c), the probability is

$$P(c) = P^4,$$

where $P$ is the probability of finding a Cantorion at any of the intersection points of the lattice. For case (b), we have

$$P(b) = 4 P^3(1-P),$$

and finally for case (a) the probability is

$$P(a) = 2 P^2(1-P)^2.$$

The total probability $P_T$ is the sum of all probabilities,

$$P_T = P^4 + 4 P^3 (1 - P) + 2 P^2 (1 - P)^2.$$ (9.1)

The physical interpretation of the three possible configurations is the following:
(a) is the minimum requirement of a topologically nonzero space;
(b) is the minimal representation of two-dimensionality, while
(c) is imposed to give a nontrivial solution for the critical probability, i.e., nonzero and different from 1.

In fact, if at a certain state, we have more empty space than Cantorions, then as we increase the renormalization procedure, we have more and more empty space, until in the end we have absolute nothingness. On the contrary, if we have more Cantorions than empty space, then as we proceed further with the renormalization process, we will reach a space continuum. At a certain critical state, we will have a dividing line, determined by a ``critical probability" $P_c.$ This probability is the fixed point of the total probability $P_T,$ given by equation (9.1).

Let us calculate this value:

$$P_c-P_c^4-4 P_c^3 (1-P_c)-2 P_c^2 (1-Pc)^2 = 0,$$

or, after excluding trivial solutions $P_c=0, P_c=1$ and dividing by $P_c (1-P_c),$

$$1-P_c- P_c^2=0,$$

and we get a noteworthy Golden Mean critical probability solution

$$P_c = \frac{1}{\phi}= \frac{{\sqrt 5 - 1}}{2}.$$

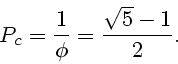
It can be proved that this value of $P_c = 1/\phi$ is an unstable fixed point of the probability map equation arising from (9.1), e.g.,

$$P_{n+1}=2 P_n^2 - P_n^4.$$ (9.2)

Finally, this renormalization transformation of a spatially chaotic two-dimensional space
spanned by two to four Cantorions on a rectangular lattice, leads to a Hausdorff dimension almost identical to that of the Sierpinski carpet, depicted in Fig. 2. As is easy to prove (see [2]), this two-dimensional set has zero measure and fractal dimension

Fig. 2.

$$D = \log 3/ \log 2 = 1.58\ldots$$

The Sierpinski carpet, together with the Cantor point-set, is believed to be a fundamental set for many two-dimensional processes. It is interesting to remark that the Cantor point-set has a fractal dimension equal to $\log 2/\log 3 = 0.63\ldots,$ that means, equal to $1/D.$ In relation to this coincidence, there is a firm conjecture that both Cantor set and Sierpinski set, are fundamental to the formation of Cantorian space and the four-dimensionality of micro space-time of bosons.²