Зафиксируем промежуток времени
![]() . Для фиксированных
фазовых векторов
. Для фиксированных
фазовых векторов
![]() и
и
![]() объекта
объекта ![]() ,
набора
,
набора ![]()
![]() и сигнала
и сигнала
![]() ,
определим в силу (2.1)-(2.6) множества
,
определим в силу (2.1)-(2.6) множества
Для фиксированных ![]() -позиции
-позиции
![]() реализаций управления
реализаций управления
![]() и сигнала
и сигнала
![]() сконструируем в силу (2.1), (4.2) и (4.3)
сконструируем в силу (2.1), (4.2) и (4.3)
![]() -позицию
-позицию
![]() преследователя
преследователя ![]() используя рекуррентные
формулы
используя рекуррентные
формулы
Аналогично определению из [4], назовем систему одношаговых соотношений (4.2)-(4.5) информационно-сопряженной для дискретной динамической системы (2.1)-(2.6). Принимая во внимание (3.1)-(3.10), (4.2)-(4.5) и условия, которые оговорены для системы (2.1)-(2.6), можно доказать [5], что справедливо следующее утверждение.
Отметим, что теорема 1 дает возможность разрабатывать
конструктивные численные алгоритмы, реализующие отображение
![]() на промежутке времени
на промежутке времени
![]() в форме последовательности
только одношаговых операций, т.е. решающих многошаговую задачу 1.
В результате этого имеется описание
в форме последовательности
только одношаговых операций, т.е. решающих многошаговую задачу 1.
В результате этого имеется описание
![]() -позиции
-позиции
![]() преследователя
преследователя ![]() , которая
формирует состояние процесса преследования-уклонения в системе
(2.1)-(2.6),
не противоречащее информации, доступной к моменту времени
, которая
формирует состояние процесса преследования-уклонения в системе
(2.1)-(2.6),
не противоречащее информации, доступной к моменту времени
![]() , и является основным элементом реализации
процесса апостериорной минимаксной фильтрации на промежутке времени
, и является основным элементом реализации
процесса апостериорной минимаксной фильтрации на промежутке времени
![]() (см. [4,5]),
генерируемым на выходе фильтра.
(см. [4,5]),
генерируемым на выходе фильтра.
Зафиксируем промежуток времени
![]() и набор
и набор
![]() , где
, где ![]() есть выпуклый, замкнутый
и ограниченный многогранник (с конечным числом вершин)
пространства
есть выпуклый, замкнутый
и ограниченный многогранник (с конечным числом вершин)
пространства ![]() . Пусть множество
. Пусть множество
![]() соответствует (4.2). Тогда из определения (4.2)
и сделанных выше предположений следует, что для всех
соответствует (4.2). Тогда из определения (4.2)
и сделанных выше предположений следует, что для всех
![]() множество
множество ![]() есть выпуклый,
замкнутый и ограниченный многогранник (с конечным числом вершин)
пространства
есть выпуклый,
замкнутый и ограниченный многогранник (с конечным числом вершин)
пространства ![]() . Известно также (см., например,
[9]), что точка
. Известно также (см., например,
[9]), что точка ![]() выпуклого, замкнутого и ограниченного
многогранника
выпуклого, замкнутого и ограниченного
многогранника ![]() представима в виде
представима в виде
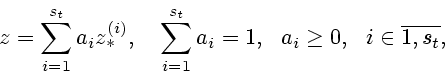
Предположим, что множество ![]() уже сконструировано.
Тогда легко доказать следующее вспомогательное утверждение.
уже сконструировано.
Тогда легко доказать следующее вспомогательное утверждение.
Тогда
![]() (здесь и ниже
(здесь и ниже
![]() есть множество всех вершин
многогранника
есть множество всех вершин
многогранника
![]() ,
и
,
и ![]() есть выпуклая оболочка этого множества).
есть выпуклая оболочка этого множества).
Сформулируем подобное утверждение для управляющей части уравнения (2.2).
Тогда
![]() .
.
Справедливо следующее утверждение.
Доказательство этой теоремы дано в [5].
Для фиксированного вектора
![]() , матрица
, матрица
![]() , фигурирующая в (2.5), по предположению имеет ранг
, фигурирующая в (2.5), по предположению имеет ранг
![]() . Пусть
. Пусть ![]() и
и
![]() есть матрица размера
есть матрица размера ![]() соответствующая
базисному минору матрицы
соответствующая
базисному минору матрицы ![]() .
Без уменьшения общности, предположим, что минор, соответствующий
матрице
.
Без уменьшения общности, предположим, что минор, соответствующий
матрице
![]() находится в верхнем левом углу
матрицы
находится в верхнем левом углу
матрицы ![]() , т.е. первые
, т.е. первые ![]() координат
координат
![]() вектора
вектора
![]() - базисные переменные
векторного уравнения (2.5).
Тогда для фиксированных векторов
- базисные переменные
векторного уравнения (2.5).
Тогда для фиксированных векторов
![]() и
и
![]() которые допустимы в силу (2.1)-(2.6),
соотношение (2.5) представимо в виде
которые допустимы в силу (2.1)-(2.6),
соотношение (2.5) представимо в виде
Принимая во внимание (4.6), (4.7),
(4.3) и введенные выше предположения,
для фиксированных и допустимых в силу (2.1)-(2.6)
векторов
![]() и
и
![]() имеем
имеем
Тогда
![]() .
.
Тогда
![]() .
.
На основании соотношения (4.8), лемм 4 и 5 аналогично доказательству теоремы 2 нетрудно показать справедливость следующего утверждения.
Тогда имеет место следующее равенство:
Используя предыдущие леммы 1-5, теоремы 1-3,
рекуррентные соотношения (4.4) и (4.5)
нетрудно показать индукцией по числу шагов
![]() ,
соответствующих промежутку времени
,
соответствующих промежутку времени
![]() , на котором рассматривается
процесс преследования-уклонения, справедливость следующего утверждения.
, на котором рассматривается
процесс преследования-уклонения, справедливость следующего утверждения.
Нетрудно доказать, что справедливо следующее утверждение.
Тогда
![]() .
.
Зафиксируем начальную позицию
![]() , где множество
, где множество ![]() есть выпуклый замкнутый
и ограниченный многогранник (с конечным числом вершин)
пространства
есть выпуклый замкнутый
и ограниченный многогранник (с конечным числом вершин)
пространства ![]() и реализации управления
и реализации управления
![]() и сигнала
и сигнала
![]()
![]() на промежутке времени
на промежутке времени
![]()
Тогда с учетом введенных выше определений и сформулированных утверждений, общая схема решения задачи 2 конструирования стратегии адаптивного минимаксного управления для процесса преследования-уклонения в дискретной динамической системе (2.1)-(2.6) может быть представлена как реализация последовательности следующих только одношаговых операций.
I. Для
![]() вычисляются следующие элементы решения.
вычисляются следующие элементы решения.
1.1. Пусть
![]() если
если ![]() , то перейти на пункт II;
иначе - перейти на пункт 1.2.
, то перейти на пункт II;
иначе - перейти на пункт 1.2.
1.2. Вектор
![]() вычисляется по рекуррентным формулам (4.4), используя вектор
вычисляется по рекуррентным формулам (4.4), используя вектор
![]() и управление
и управление
![]() .
.
1.3. Область достижимости
![]() вычисляется при предположении, что
вычисляется при предположении, что
![]() есть выпуклый замкнутый и
ограниченный многогранник (с конечным числом вершин), который уже
определен
есть выпуклый замкнутый и
ограниченный многогранник (с конечным числом вершин), который уже
определен
![]() , т.е. известно множество
, т.е. известно множество
![]() всех вершин многогранника
(общая схема построения этого множества описывается в пункте
III алгоритма). На основании изложенного выше, эта область
может быть сконструирована с использованием следующей схемы.
всех вершин многогранника
(общая схема построения этого множества описывается в пункте
III алгоритма). На основании изложенного выше, эта область
может быть сконструирована с использованием следующей схемы.
1.3.1. Используя известные матрицы ![]() и
и ![]() ,
множества
,
множества
![]() и
и
![]() всех вершин многогранников
всех вершин многогранников
![]() и
и ![]() соответственно,
конструируем следующие множества
соответственно,
конструируем следующие множества
1.3.2. Пусть
![]() ; тогда рассматривается следующая
задача линейного программирования.
; тогда рассматривается следующая
задача линейного программирования.
З а д а ч а 3. Для фиксированных
![]() и набора переменных
и набора переменных
![]() требуется установить
совместность следующей системы линейных соотношений:
требуется установить
совместность следующей системы линейных соотношений:
Эта задача решается с помощью модифицированного
симплекс-метода (см., например, [10]), который используется
для задачи линейного программирования с ограничениями
(4.9) и поиска минимума целевой функции
![]() достаточно произвольного вида, например,
достаточно произвольного вида, например,
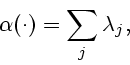
Отметим, что такой выбор целевой функции значительно упрощает
проверку совместности ограничений (4.9)
на первом шаге модифицированного симплекс-метода. При этом из свойств
системы (4.9) следует, что если она совместна, то точка
![]() не является вершиной
многогранника
не является вершиной
многогранника
![]() ;
в противном случае имеем
;
в противном случае имеем
![]() .
.
Тогда, решая задачу 3 для всех значений параметра
![]() , найдем все вершины многогранника
, найдем все вершины многогранника
![]() , так как
в силу теоремы 2 имеет место равенство
, так как
в силу теоремы 2 имеет место равенство
![]() .
.
II. Для фиксированных
![]() и
и
![]() множество
множество
![]() вычисляется в соответствии со следующей схемой.
вычисляется в соответствии со следующей схемой.
2.1. В соответствии с изложенным выше по известной матрице
![]() находится матрица
находится матрица
![]() размера
размера
![]() , которая существует в силу сделанных
предположений и имеет вид
, которая существует в силу сделанных
предположений и имеет вид
2.2. Используя матрицы
![]() и
и ![]() , множества
, множества
![]() и
и
![]() всех вершин многогранников
всех вершин многогранников
![]() и
и ![]() соответственно, конструируем множества
соответственно, конструируем множества
2.3. Пусть
![]() ; тогда, решая задачу 3
для этого множества и для всех значений параметра
; тогда, решая задачу 3
для этого множества и для всех значений параметра
![]() , найдем все вершины многогранника
, найдем все вершины многогранника
![]() ,
так как в силу теоремы 3 имеет место равенство
,
так как в силу теоремы 3 имеет место равенство
![]()
![]()
III. Используя модифицированные рекуррентные формулы
(4.5), вычисляем следующие множества:
3.1. Используя множества
![]() или
или
![]() всех вершин многогранников
всех вершин многогранников
![]() или
или
![]() соответственно, которые известны к началу этого пункта,
вычисляем крайние опорные гиперплоскости [9]
соответствующего многогранника.
соответственно, которые известны к началу этого пункта,
вычисляем крайние опорные гиперплоскости [9]
соответствующего многогранника.
В связи с этим напомним, что опорной гиперплоскостью
выпуклого многогранника
![]() называется гиперплоскость вида
называется гиперплоскость вида
![]() ,
где
,
где
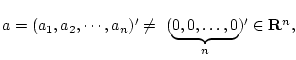
![]() для всех
для всех ![]() и
и
![]() хотя бы для одного
хотя бы для одного ![]() .
Если опорная гиперплоскость содержит
.
Если опорная гиперплоскость содержит ![]() аффинно-независимых
[9] точек множества
аффинно-независимых
[9] точек множества ![]() , то она называется
крайней опорной гиперплоскостью этого множества.
, то она называется
крайней опорной гиперплоскостью этого множества.
3.2. Крайние опорные гиперплоскости многогранника
![]()
![]() вычисляется с использованием известного множества
вычисляется с использованием известного множества
![]() всех его вершин.
всех его вершин.
3.3. Используя сконструированные гиперплоскости многогранников
![]() или
или
![]() и
и
![]() находим общее решение системы
неравенств, состоящей из всех неравенств, порожденных
крайними опорными гиперплоскостями этих многогранников,
соответствующих фиксированному моменту времени
находим общее решение системы
неравенств, состоящей из всех неравенств, порожденных
крайними опорными гиперплоскостями этих многогранников,
соответствующих фиксированному моменту времени
![]() которое описывает в частном случае
множество
которое описывает в частном случае
множество
![]() - всех вершин многогранника
- всех вершин многогранника
![]()
В результате реализации предыдущих пунктов для всех
![]() вычисляется
вычисляется ![]() -позиция
-позиция
![]()
![]() преследователя
преследователя ![]() ,
где
,
где
![]() и
и
![]()
![]() есть информационное множество
процесса апостериорной минимаксной фильтрации для
дискретной динамической системы (2.1)-(2.6).
Отметим, что это есть множество все допустимых реализаций
фазовых векторов
есть информационное множество
процесса апостериорной минимаксной фильтрации для
дискретной динамической системы (2.1)-(2.6).
Отметим, что это есть множество все допустимых реализаций
фазовых векторов
![]() объекта
объекта ![]() в момент времени
в момент времени ![]() , которые
совместимы со всей информацией об этой системе,
известной преследователю
, которые
совместимы со всей информацией об этой системе,
известной преследователю ![]() на промежутке времени
на промежутке времени
![]() .
.
IV. В этом пункте вычисляются все параметры
стратегии адаптивного минимаксного управления
![]() преследователя
преследователя ![]() для некоторого
момента времени
для некоторого
момента времени
![]() .
.
Эта процедура реализуется следующим образом.
4.1. Используя известные матрицы ![]() и
и ![]() вектор
вектор
![]() и множество
и множество
![]() всех вершин
многогранника
всех вершин
многогранника ![]() конструируем следующие множества:
конструируем следующие множества:
4.2. Пусть
![]() , тогда, решая задачу 3
для этого множества и для всех значений параметра
, тогда, решая задачу 3
для этого множества и для всех значений параметра
![]() найдем все вершины многогранника
найдем все вершины многогранника
![]() ,
так как из теоремы 5 следует справедливость равенства
,
так как из теоремы 5 следует справедливость равенства
![]() .
.
Используя это множество, можно вычислить также множество
![]() всех вершин многогранника
всех вершин многогранника
![]() (например, путем решения соответствующей
задачи 3) и множество всех его крайних
опорных гиперплоскостей.
(например, путем решения соответствующей
задачи 3) и множество всех его крайних
опорных гиперплоскостей.
Тогда множество
![]() описывается следующей системой
линейных неравенств
описывается следующей системой
линейных неравенств
4.3. Используя известные матрицы ![]() и
и ![]() ,
множества
,
множества
![]() и
и
![]() всех вершин многогранников
всех вершин многогранников
![]() и
и ![]() соответственно, сконструируем множества
соответственно, сконструируем множества
Пусть
![]() , тогда,
решая задачу 3 для этого множества и для всех значений
параметра
, тогда,
решая задачу 3 для этого множества и для всех значений
параметра
![]() ,
найдем все вершины многогранника
,
найдем все вершины многогранника
![]() ,
так как из теоремы 2 следует справедливость равенства
,
так как из теоремы 2 следует справедливость равенства
![]() .
.
4.4. Используя множество
![]() всех вершин многогранника
всех вершин многогранника
![]() , сформированного в предыдущем пункте,
можно вычислить множество
, сформированного в предыдущем пункте,
можно вычислить множество
![]() всех вершин многогранника
всех вершин многогранника
![]() и ввести для
и ввести для
![]() функционалы
функционалы
4.5. Вводится дополнительная переменная
![]() и используя функционалы
и используя функционалы
![]() и соотношения
(4.11) конструируется система выпуклых и линейных неравенств
и соотношения
(4.11) конструируется система выпуклых и линейных неравенств
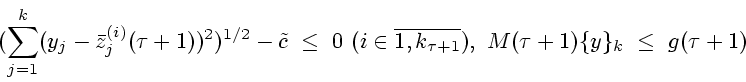
4.6. Рассматривается следующая задача выпуклого
программирования
Эта задача решается с использованием, например, алгоритма метода Зойтендейка (случай нелинейных ограничений-неравенств) (см., например, [10]).
Пусть
![]()
![]() есть решение этой задачи, которое удовлетворяет соотношению
есть решение этой задачи, которое удовлетворяет соотношению
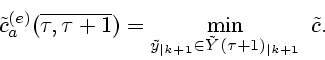
Тогда для
![]() ,
используя приведенные выше леммы 1-6, теоремы 1-5 и соотношения
(4.10)-(4.12)
нетрудно доказать справедливость следующих равенств:
,
используя приведенные выше леммы 1-6, теоремы 1-5 и соотношения
(4.10)-(4.12)
нетрудно доказать справедливость следующих равенств:
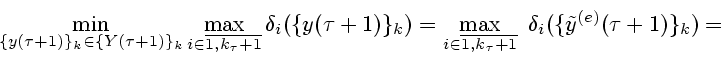
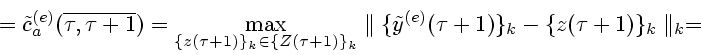
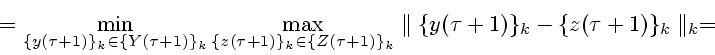
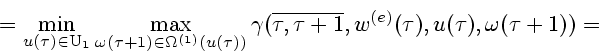
Используя этот алгоритм с пункта I до пункта IV, и снова с пункта I
для всех моментов времени
![]() и
всех
и
всех ![]() -позиций
-позиций
![]() можно сконструировать следующие множества
можно сконструировать следующие множества
Тогда определим стратегию управления
![]() преследователя
преследователя ![]() для процесса
преследования-уклонения (2.1)-(2.6) на промежутке
времени
для процесса
преследования-уклонения (2.1)-(2.6) на промежутке
времени
![]() из класса допустимых
стратегий управления
из класса допустимых
стратегий управления ![]() , которая формально
описывается следующими соотношениями:
, которая формально
описывается следующими соотношениями:
1) для всех
![]() и
и
![]() -позиций
-позиций
![]()
![]()
![]() пусть
пусть
2) для всех
![]() и
и ![]() -позиций
-позиций
![]() пусть
пусть
Пусть набор
![]() состоящий из реализаций управления
состоящий из реализаций управления
![]() преследователя
преследователя ![]() и сигнала
и сигнала
![]() соответственно, сформирован в результате
использования этой стратегии на промежутке времени
соответственно, сформирован в результате
использования этой стратегии на промежутке времени
![]() и такой, что
и такой, что
![]() и
и
![]() удовлетворяют соотношению
(4.13) при
удовлетворяют соотношению
(4.13) при
![]() Тогда можно вычислить следующее число
Тогда можно вычислить следующее число
Из приведенного выше алгоритма и соотношений (4.12)-(4.16) получим следующее утверждение, которое является основным результатом данной работы.
Необходимо также отметить, что для реализаций управления
![]() преследователя
преследователя ![]() и сигнала
и сигнала
![]()
![]() которые являются результатом использования стратегии
адаптивного минимаксного управления
которые являются результатом использования стратегии
адаптивного минимаксного управления
![]() на промежутке времени
на промежутке времени
![]() и для всех
и для всех
![]() удовлетворяют
соотношению (4.13), для всех допустимых реализаций
сигналов
удовлетворяют
соотношению (4.13), для всех допустимых реализаций
сигналов
![]() для всех допустимых реализаций управления
для всех допустимых реализаций управления
![]() преследователя
преследователя ![]() существует сигнал
существует сигнал
![]() такой,
что для всех
такой,
что для всех
![]() в силу (3.6) и (4.13)
имеют место следующие соотношения:
в силу (3.6) и (4.13)
имеют место следующие соотношения: