3. Постановка задачи

Введем ряд определений, которые необходимы для строгой математической формулировки задачи адаптивного минимаксного управления для процесса преследования-уклонения в дискретной динамической системе (2.1)-(2.6).

Для фиксированных $n\in\bf N$ и $\overline{\tau,\vartheta}\subseteq \overline{0,\rm T}~(\tau\le\vartheta)$ введем ${\bf S}_n(\overline{\tau,\vartheta})$ - метрическое пространство функций целочисленного аргумента $\varphi: \overline{\tau,\vartheta} \longrightarrow {\bf R}^n$, где метрика $\rho_n$ определяется следующим образом:

$$\rho_n(\varphi_1(\cdot),\varphi_2(\cdot)) =\max_{t\in \overli... ...u,\vartheta}}\parallel \varphi_1(t) - \varphi_2(t) \parallel_n$$

$$((\varphi_1(\cdot),\varphi_2(\cdot))\in {\bf S}_n(\overline{\tau,\vartheta})\times {\bf S}_n(\overline{\tau,\vartheta})),$$

и через $\mbox{comp}({\bf S}_n(\overline{\tau,\vartheta}))$ обозначим множество всех непустых и компактных в смысле этой метрики подмножеств пространства ${\bf S}_n(\overline{\tau,\vartheta})$. Здесь $\parallel\cdot\parallel_n$ есть евклидова норма в ${\bf R}^n$.

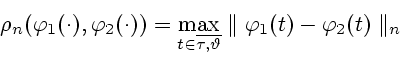
Используя ограничение (2.3), определим множество $U(\overline{\tau,\vartheta})\in$
$\mbox{comp}({\bf S}_{p}(\overline{\tau,\vartheta-1}))$ допустимых управлений $u(\cdot)=\{u(t)\}_{t\in \overline{\tau,\vartheta -1}}$ преследователя $P$ на промежутке времени $\overline{\tau,\vartheta}\subseteq \overline{0,\rm T}$ $(\tau<\vartheta)$ соотношением

$$U(\overline{\tau,\vartheta}) = \{u(\cdot):~ u(\cdot)\in{\bf S... ...forall~ t\in \overline{\tau,\vartheta-1},~u(t)\in {\rm U}_1\}.$$

На основании ограничений (2.3) и (2.6) аналогичным образом определим множества $V(\overline{\tau,\vartheta}) \in\mbox{comp}({\bf S}_q(\overline{\tau,\vartheta-1}))$ и ${\Xi}(\overline{\tau,\vartheta})\in \mbox{comp}({\bf S}_{l}(\overline{\tau+1,\vartheta}))$ допустимых управлений $v(\cdot)=\{v(t)\}_{t\in\overline{\tau,\vartheta-1}}$ уклоняющегося $E$ и допустимых ошибок измерений ${\xi}(\cdot)= \{{\xi}(t)\}_{t\in\overline{\tau+1,\vartheta}}$ сигнала на промежутке времени $\overline{\tau,\vartheta}$ соответственно.

Обозначим через ${\hat\Omega}(\overline{\tau,\vartheta}) \subset{\bf S}_{m}(\overline{\tau+1,\vartheta})$ множество допустимых, в силу (2.1)-(2.6), реализаций сигнала ${\omega}(\cdot)= \{{\omega}(t)\}_{ t\in\overline{\tau +1,\vartheta}}$ на промежутке времени $\overline{\tau,\vartheta}$.

Назовем набор $w(\tau)=\{\tau,y(\tau),Z(\tau)\}\in\overline{0,\rm T} \times{\bf R}^{r}\times\mbox{comp}({\bf R}^s)$ ($Z(\tau)$ есть множество допустимых фазовых состояний $z(\tau)\in{\bf R}^{s}$ объекта $II$ в момент времени $\tau$, $w(0)=w_0=\{0,y_0,Z_0\}, w^*_0=\{0,y_0,Z^*_0\})$ - $\tau$-позицией преследователя $P$ в дискретной динамической системе (2.1)-(2.6), где множество $Z^*_0$ непусто и определяется соотношением

$$Z^*_0 = \{z_0 :~z_0\in Z_0,~ \exists~\tilde\xi_0\in\Xi_1,~ \omega_0 = E(y_0)z_0+F(0)\tilde\xi_0\}.$$

Для всех $\tau\in\overline{0,\rm T}$ определим также множество ${\hat W}(\tau)=\{\tau\}\times{\bf R}^{r}\times \mbox{comp}({\bf R}^{s})~ ({\ha... ..._0 :~w_0=\{0,y_0,Z_0\}\in \{0\}\times{\bf R}^r\times{\rm comp}({\bf R}^{s})\})$ всех допустимых $\tau$-позиций преследователя $P$.

Далее, для фиксированных промежутка времени $\overline{\tau,\vartheta}\subseteq\overline{0,\rm T}~ (\tau<\vartheta)$, допустимых в силу (2.1)-(2.6) реализаций $\tau$-позиции $w(\tau)=\{\tau,y(\tau),Z(\tau)\}$
$\in {\hat W}(\tau)$, управления $u(\cdot)\in U(\overline{\tau,\vartheta})$ преследователя $P$ и сигнала $\omega(\cdot) \in{\hat \Omega}(\overline{\tau,\vartheta})$ определим через $R(\overline{\tau,\vartheta},w(\tau),u(\cdot), \omega(\cdot))$ множество всех пар $({\tilde z}(\tau),$
${\tilde v}(\cdot))\in Z(\tau)\times V(\overline{\tau,\vartheta})$ совместимых [1]-[5] с этой информацией на промежутке времени $\overline{\tau,\vartheta}:$

$$R(\overline{\tau,\vartheta},w(\tau),u(\cdot), \omega(\cdot))... ...ilde v}(\cdot))\in Z(\tau)\times V(\overline{\tau,\vartheta}),$$

$$\forall~t\in \overline{\tau+1,\vartheta},~ \exists~{\tilde\x... ...Xi_{1},~ {\omega}(t) = E(y(t)){\tilde z}(t)+F(t){\tilde\xi}(t)$$

$$(y(t)=y_t(\overline{\tau,\vartheta},y(\tau),u(\cdot)),~ {\ti... ...rline{\tau,\vartheta}, {\tilde z}(\tau),{\tilde v}(\cdot)))\},$$ (3.1)

где $y_{t}(\overline{\tau,\vartheta},y(\tau),u(\cdot))$ и $z_{t}(\overline{\tau,\vartheta},{\tilde z}(\tau),{\tilde v}(\cdot))$ определяют сечения движений объектов $I$ и $II$ на промежутке времени $\overline{\tau,\vartheta}$ в момент времени $t\in\overline{\tau+1,\vartheta}$ соответственно. В силу (2.1) и (2.2) движения объектов $I$ и $II$ порождены соответственно парами $(y(\tau),u(\cdot))$ и $({\tilde z}(\tau),{\tilde v}(\cdot))$.

Назовем множество

$$Z^{(e)}_{\vartheta}(\overline{\tau,\vartheta}, w(\tau),u(\cd... ...ot)) = \{z^{(e)}(\vartheta) :~ z^{(e)}(\vartheta)\in{\bf R}^s,$$

$$z^{(e)}(\vartheta)=z_{\vartheta}(\overline{\tau,\vartheta}, ... ...R(\overline{\tau,\vartheta},w(\tau), u(\cdot),\omega(\cdot))\}$$ (3.2)

информационным множеством преследователя $P$ [1]-[5] в процессе апостериорной минимаксной фильтрации для дискретной динамической системы (2.1)-(2.6) на промежутке времени $\overline{\tau,\vartheta}$, соответствующим моменту времени $\vartheta$ и набору $(w(\tau),u(\cdot),{\omega}(\cdot))\in {\hat W}(\tau) \times U(\overline{\tau,\vartheta})\times {\hat \Omega}(\overline{\tau,\vartheta})$. Следует отметить, что это есть множество всех допустимых реализаций фазовых векторов объекта $II$ в момент времени $\vartheta$, которые совместимы со всей информацией об этой системе, известной преследователю $P$ на промежутке времени $\overline{\tau,\vartheta}$.

Для фиксированного промежутка времени $\overline{\tau,\vartheta}\subseteq\overline{0,\rm T}~ (\tau<\vartheta)$,
$\tau$-позиции $w(\tau)= \{\tau,y(\tau),Z(\tau)\}\in {\hat W}(\tau)$ преследователя $P$ и его управления $u(\cdot)\in U(\overline{\tau,\vartheta})$ определим следующие множества:

$$\Omega(\overline{\tau,\vartheta},w(\tau),u(\cdot)) = \{\omeg... ...) :~\omega(\cdot) \in{\hat \Omega}(\overline{\tau,\vartheta}),$$

$$\forall~t\in\overline{\tau+1,\vartheta}\ \ {\omega}(t)=E(y(t))z(t)+F(t){\xi}(t)$$

$$(y(t)=y_{t}(\overline{\tau,\vartheta},y(\tau), u(\cdot)),~\ z(t)=z_{t}(\overline{\tau,\vartheta},z(\tau), v(\cdot))),$$

$${\xi}(t)\in {\Xi}_1,~\ (z(\tau),v(\cdot))\in Z(\tau)\times V(\overline{\tau,\vartheta})\};$$ (3.3)

$$W(\tau,w(\tau),\vartheta,u(\cdot)) = \{w(\vartheta) :~ w(\vartheta)\in {\hat W}(\vartheta),$$

$$w(\vartheta)=\{\vartheta,y(\vartheta),Z(\vartheta)\},~\ y(\v... ...a)=y_{\vartheta}(\overline{\tau,\vartheta},y(\tau), u(\cdot)),$$

$$Z(\vartheta) = Z^{(e)}_{\vartheta} (\overline{\tau,\vartheta... ...ot)\in {\Omega}(\overline{\tau,\vartheta}, w(\tau),u(\cdot))\}$$ (3.4)

и назовем их множеством допустимых сигналов на промежутке времени $\overline{\tau,\vartheta}$ и множеством допустимых $\vartheta$-позиций преследователя $P$ соответственно, которые соответствуют $\tau$-позиции $w(\tau)$ и управлению $u(\cdot)$.

Используя определения (3.1)-(3.4) и условия, оговоренные для системы (2.1)-(2.6), аналогично результатам, полученным в работе [5], можно доказать, что справедливо следующее вспомогательное утверждение.

Лемма 1   Для фиксированного промежутка времени $\overline{\tau,\vartheta}\subseteq \overline{0,\rm T}$
$(\tau<\vartheta)$ и для возможной в силу $(\ref{eq1})$-$(\ref{eq6})$ реализации набора $(w^*_0,u(\cdot),$
$\omega(\cdot))\in {\hat W}_0\times U(\overline{0,\vartheta})\times \Omega(\overline{0,\vartheta},w_0,u(\cdot))$, соответствующего промежутку времени $\overline{0,\vartheta}$, справедливы следующие соотношения:

$$R(\overline{0,\vartheta},w^*_0,u(\cdot), \omega(\cdot)) = R(... ...artheta},w_*(\tau),{\tilde u}(\cdot), {\tilde \omega}(\cdot));$$ (3.5)

$$Z^{(e)}_{\vartheta}(\overline{0,\vartheta}, w^*_0,u(\cdot),\... ...artheta}, w_*(\tau),{\tilde u}(\cdot),{\tilde \omega}(\cdot));$$ (3.6)

$$\Omega(\overline{0,\vartheta},w^*_0,u(\cdot)) = \Omega(\overline{\tau,\vartheta}, w_*(\tau),{\tilde u}(\cdot));$$ (3.7)

$$W(0,w^*_0,\vartheta,u(\cdot)) = W(\tau,w_*(\tau),\vartheta,{\tilde u}(\cdot)).$$ (3.8)

Здесь для $\tau$-позиции $w_{*}(\tau)=\{\tau,y_{*}(\tau),$ $Z^{(e)}_*(\tau)\}\in {\hat W}(\tau)$ преследователя $P$ и его управления ${\tilde u}(\cdot)\in U(\overline{\tau,\vartheta})$ должны выполняться следующие соотношения:

$$y_{*}(\tau)=y_{\tau}(\overline{0,\tau}, y_0,u_{*}(\cdot))\in... ...)=\{u(t)\}_{t\in\overline{0,\tau-1}} \in U(\overline{0,\tau});$$

$$Z^{(e)}_*(\tau) = Z^{(e)}_{\tau}(\overline{0,\tau}, w^*_0,u_{*}(\cdot),\omega_{*}(\cdot))\in \mbox {comp}({\bf R}^s);$$

$$\omega_{*}(\cdot)=\{{\omega}(t)\}_{t\in\overline{1,\tau}}\in \Omega(\overline{0,\tau},w^*_0,u_{*}(\cdot));$$

$${\tilde u}(\cdot)=\{u(t)\}_{t\in \overline{\tau,\vartheta-1}... ...\tau+1,\vartheta}}\in {\hat\Omega}(\overline{\tau,\vartheta}).$$

Пусть ${\bf F}_{\overline{\tau,\vartheta}}: {\hat W}(\tau)\times U(\overline{\tau,\va... ...times {\hat \Omega} (\overline{\tau,\vartheta})\rightarrow {\hat W}(\vartheta)$ есть многошаговое отображение, ставящее в соответствие набору $(w(\tau),u(\cdot),\omega(\cdot)) \in {\hat W}(\tau)\times U(\overline{\tau,\vartheta})\times {\hat \Omega}(\overline{\tau,\vartheta})$ $\vartheta$-позицию $w^{(e)}(\vartheta)=\{\vartheta,y^{(e)}(\vartheta), Z^{(e)}(\vartheta)\}\in {\hat W}(\vartheta)$, а именно

$$w^{(e)}(\vartheta) = \{\vartheta,y^{(e)}(\vartheta), Z^{(e)}... ..._{\overline {\tau,\vartheta}}(w(\tau),u(\cdot),\omega(\cdot)),$$ (3.9)

где

$$y(\vartheta)=y_{\vartheta}(\overline{\tau,\vartheta}, y(\tau... ...ta} (\overline{\tau,\vartheta},w(\tau),u(\cdot),\omega(\cdot))$$

$$(w(\tau)=\{\tau,y(\tau),Z(\tau)\},~w(0)=w^*_0).$$ (3.10)

Далее, сформулируем для преследователя $P$ следующую многошаговую задачу построения его допустимых позиций в динамической системе (2.1)-(2.6).

З а д а ч а 1. Для фиксированной реализации набора $(w(\tau),u(\cdot),\omega(\cdot))$
$\in {\hat W}(\tau)\times U(\overline{\tau,\vartheta})\times {\hat \Omega}(\overline{\tau,\vartheta}) (w(0)=w^*_0),$ который соответствует дискретной динамической системе (2.1)-(2.6) и известен в конце промежутка времени $\overline{\tau,\vartheta}\subseteq\overline{0,\rm T}~ (\tau<\vartheta)$, требуется определить многошаговое отображение ${\bf F}_{\overline{\tau,\vartheta}}$ как реализацию последовательности только одношаговых операций.

В следующем разделе описывается общая рекуррентная схема для решения этой задачи и будет иметься возможность построения информационного множества $Z^{(e)}_{\vartheta}(\overline{\tau,\vartheta}, w(\tau),u(\cdot),\omega(\cdot))\subset {\bf R}^s$, которое является основным элементом решения задачи апостериорной минимаксной фильтрации [4,5] для системы (2.1)-(2.6) и будет необходимо для решения рассматриваемой задачи преследования-уклонения.

Тогда, для оценивания качества процесса преследования-уклонения в динамической системе (2.1)-(2.6) на промежутке времени $\overline{\tau,\vartheta}\subseteq \overline{0,\rm T}$ преследователем $P$ определим функционал   $\gamma :~{\hat W}(\tau)\times U(\overline{\tau,\vartheta})\times {\hat \Omega}(\overline{\tau,\vartheta}) \rightarrow {\bf R}^{1}$ таким образом, что для реализации набора $(w(\tau),u(\cdot),\omega(\cdot)) \in {\hat W}(\tau)\times U(\overline{\tau,\vartheta})\times {\hat \Omega}(\overline{\tau,\vartheta})$ его значение определяется соотношением

$$\gamma(\overline{\tau,\vartheta},w(\tau),u(\cdot),\omega(\cd... ...} \parallel \{y(\vartheta)\}_k - \{z(\vartheta)\}_k\parallel_k$$

$$(\{y(\vartheta)\}_k=\{y_{\vartheta} (\overline{\tau,\vartheta},y(\tau),u(\cdot))\}_k,$$

$$\{Z^{(e)}(\vartheta)\}_{k} = \{Z^{(e)}_{\vartheta} (\overline{\tau,\vartheta},w(\tau),u(\cdot),\omega(\cdot))\}_{k}).$$ (3.11)

Здесь и ниже для $n\in{\bf N}, k\in\overline{1,n}, x=(x_1,x_2,\cdots,x_{n})^\prime\in{\bf R}^{n}$ и $X\subset{\bf R}^{n}$ выражения $\{x\}_k=(x_1,x_2,\cdots,x_k)^\prime \in{\bf R}^k$ и $\{X\}_k=\{g: g\in{\bf R}^k, g=\{x\}_k, x\in X\} \subset{\bf R}^k$ есть $k$-проекция вектора $x$ и $k$-проекция множества $X$ соответственно; $w(\tau)=\{\tau,y(\tau),Z(\tau)\}\in {\hat W}(\tau)~(w(0)=w_{0})$.

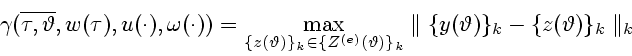
Далее, введем несколько определений.

Допустимой стратегией адаптивного управления ${\bf U}$ преследователя $P$ для процесса преследования-уклонения (2.1)-(2.6) на промежутке времени $\overline{0,\rm T}$ будем называть отображение ${\bf U}: {\hat W}(\tau)\rightarrow {\rm U}_1$, которое каждому моменту времени $\tau\in\overline{0,{\rm T}-1}$ и возможной реализации $\tau$-позиции $w(\tau)=\{\tau,y(\tau),Z(\tau)\}\in {\hat W}(\tau) (w(0)=w_0)$ назначает множество ${\bf U}(w(\tau))\subseteq {\rm U}_1$ управлений $u(\tau)\in {\rm U}_1$ преследователя $P$. Обозначим множество всех допустимых стратегий адаптивного управления преследователя $P$ для этого процесса через ${\bf U}^*$.

Определим стратегию адаптивного минимаксного управления для процесса преследования-уклонения (2.1)-(2.6) как реализацию специфической стратегии адаптивного управления ${\bf U}^{(e)}_{a}= {\bf U}^{(e)}_{a}(w(\tau))\in {\bf U}^{*}~ (\tau\in\overline{0,{\rm T}-1},$
$w(\tau)\in {\hat W}(\tau), w(0)=w_{0})$ из класса допустимых стратегий адаптивного управления ${\bf U}^*$, которая формально описывается следующими соотношениями:

1) для всех $\tau\in\overline{0,{\rm T}-1}$ и $\tau$-позиций $w^{(e)}(\tau)= \{\tau,y^{(e)}(\tau),Z^{(e)}(\tau)\} \in W(0,w_{0},\tau,u^{(e)}_{\tau}(\cdot))$ $(w^{(e)}(0)=w^*_{0})$ пусть

$${\bf U}^{(e)}_{a}(w^{(e)}(\tau))= {\bf U}^{(e)}(w^{(e)}(\tau))\subseteq {\rm U}_1;$$ (3.12)

2) для всех $\tau\in\overline{0,{\rm T}-1}$ и $\tau$-позиций $w^{*}(\tau)=\{\tau,y^{*}(\tau),Z^{*}(\tau)\}\in \{{\hat W}(\tau)\setminus W(0,w_{0},\tau,u^{(e)}_{\tau}(\cdot))\}~(w^{*}(0)\ne w^*_0)$ пусть

$${\bf U}^{(e)}_{a}(w^{*}(\tau))={\rm U}_1.$$ (3.13)

Здесь $w^*_0=\{0,y_0,Z^*_0\}\in {\hat W}_{0};$ для допустимых истории реализаций на промежутке времени $\overline{0,\tau}~(\tau\ge 1)$ управления $u^{(e)}_{\tau}(\cdot)=\{u^{(e)}(t)\}_{t\in\overline{0,\tau-1}}\in U(\overline{0,\tau})$ преследователя $P$ и сигнала ${\omega}^{(e)}_{\tau}(\cdot)= \{\omega^{(e)}(t)\}_{t\in\overline{1,\tau}}\in {\Omega}(\overline{0,\tau},w^*_{0},$
$u^{(e)}_{\tau}(\cdot))$ $\tau$-позиция $w^{(e)}(\tau)= \{\tau,y^{(e)}(\tau),Z^{(e)}(\tau)\}$ формируется согласно (3.9), а именно

$$w^{(e)}(\tau) = \{\tau,y^{(e)}(\tau),Z^{(e)}(\tau)\} = {\bf ... ...}} (w^*_0,u^{(e)}_{\tau}(\cdot),{\omega}^{(e)}_{\tau}(\cdot));$$

множество ${\bf U}^{(e)}(w^{(e)}(\tau))$ должно удовлетворять следующему соотношению

$${\bf U}^{(e)}(w^{(e)}(\tau)) = \{u^{(e)}(\tau) :~u^{(e)}(\tau)\in {\rm U}_1,$$

$$\max_{\omega(\tau+1)\in \Omega^{(1)}(u^{(e)}(\tau))} \gamma(... ...ne{\tau,\tau+1}, w^{(e)}(\tau),u^{(e)}(\tau),\omega(\tau+1)) =$$

$$= \min_{u(\tau)\in {\rm U}_1} \max_{\omega(\tau+1)\in \Omega... ...,u(\tau),\omega(\tau+1)) = c^{(e)}_{a}(\overline{\tau,\tau+1})$$

$$(\Omega^{(1)}(u^{(e)}(\tau))= \Omega(\overline{\tau,\tau+1},w^{(e)}(\tau),u^{(e)}(\tau)),$$

$$\Omega^{(2)}(u(\tau))=\Omega(\overline{\tau,\tau+1}, w^{(e)}(\tau),u(\tau)))\},$$ (3.14)

где функционал $\gamma$ определяется соотношением (3.11) и число $c^{(e)}_{a}(\overline{\tau,\tau+1})$ есть оптимальный гарантированный результат, соответствующий реализации стратегии адаптивного минимаксного управления ${\bf U}^{(e)}_{a}\in {\bf U}^*$ преследователя $P$ на промежутке времени $\overline{\tau,\tau+1}$. Из сделанных выше предположений для дискретной динамической системы (2.1)-(2.6) и свойств функционала $\gamma$ следует, что для всех моментов времени $\tau\in\overline{0,{\rm T}-1}$ и $\tau$-позиций $w(\tau)\in {\hat W}(\tau)~(w(0)=w_0)$ множества ${\bf U}^{(e)}_{a}(w(\tau))$ непусты.

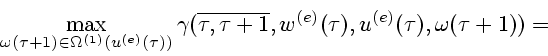
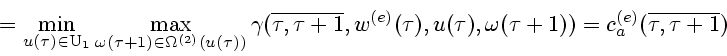
Пусть реализации управления $u^{(e)}(\cdot)= \{u^{(e)}(t)\}_{t\in\overline{0,{\rm T}-1}}\in U(\overline{0,{\rm T}})$ преследователя $P$ и сигнала $\omega^{(e)}(\cdot)= \{\omega^{(e)}(t)\}_{t\in\overline{1,\rm T}}\in {\Omega}(\overline{0,{\rm T}},w^*_{0},u^{(e)}(\cdot)),$ являются результатом использования стратегии адаптивного минимаксного управления ${\bf U}^{(e)}_{a}\in {\bf U}^*$ на промежутке времени $\overline{0,\rm T}$ и сигнал ${\omega}^{(e)}({\rm T})\in {\Omega}(\overline{{\rm T}-1,{\rm T}},w^{(e)}({\rm T}-1), u^{(e)}({\rm T}-1))$ удовлетворяет следующему соотношению

$$\gamma(\overline{{\rm T}-1,{\rm T}},w^{(e)}({\rm T}-1), u^{(e)}({\rm T}-1),{\omega}^{(e)}({\rm T})) =$$

$$= \max_{{\omega}({\rm T})\in {\Omega}(\overline{{\rm T}-1,{\... ...T}},w^{(e)}({\rm T}-1), u^{(e)}({\rm T}-1),{\omega}({\rm T})),$$

где $({\rm T}-1)$-позиция преследователя $P$,

$$w^{(e)}({\rm T}-1)=\{{\rm T}-1,y^{(e)}({\rm T}-1), Z^{(e)}({\rm T}-1)\}\in~W(0,w_{0},{\rm T}-1, u_{{\rm T}-1}^{(e)}(\cdot))$$

$$(y^{(e)}({\rm T}-1)=y_{{\rm T}-1}(\overline{0,{\rm T}-1}, y_{0},u_{{\rm T}-1}^{(e)}(\cdot))),$$

$$Z^{(e)}({\rm T}-1) =Z^{(e)}_{{\rm T}-1}(\overline{0,{\rm T}-1... ...u_{{\rm T}-1}^{(e)}(\cdot), {\omega}_{{\rm T}-1}^{(e)}(\cdot)),$$

$$u_{{\rm T}-1}^{(e)}(\cdot)= \{u^{(e)}(t)\}_{t\in\overline{0,{\rm T}-2}}\in U(\overline{0,{\rm T}-1}),$$

$${\omega}_{{\rm T}-1}^{(e)}(\cdot)= \{{\omega}^{(e)}(t)\}_{t\... ...}(\overline{0,{\rm T}-1}, w^*_{0},u^{(e)}_{{\rm T}-1}(\cdot)).$$

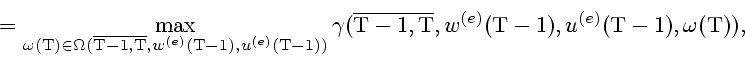
Тогда назовем число

$$c^{(e)}_{a}(\overline{0,\rm T}) = \gamma(\overline{0,\rm T}, w^*_0,u^{(e)}(\cdot),\omega^{(e)}(\cdot))$$

оптимальным гарантированным результатом, соответствующим реализации стратегии адаптивного минимаксного управления ${\bf U}^{(e)}_{a}\in {\bf U}^*$ преследователя $P$ на промежутке времени $\overline{0,\rm T}$.

Принимая во внимание приведенные выше определения, можно сформулировать основную задачу адаптивного минимаксного управления для процесса преследования-уклонения в дискретной динамической системе (2.1)-(2.6).

З а д а ч а 2. Для начальной позиции $w(0)=w_0= \{0,y_0,Z_{0}\}\in {\hat W}_0$ преследователя $P$ в дискретной динамической системе (2.1)-(2.6) требуется определить его стратегию адаптивного минимаксного управления ${\bf U}^{(e)}_{a}\in {\bf U}^*$ и оптимальный гарантированный результат $c^{(e)}_{a}(\overline{0,\rm T})$, соответствующий реализации этой стратегии на промежутке времени $\overline{0,\rm T}$ для процесса преследования-уклонения, как реализацию последовательности только одношаговых операций.

В следующем разделе описывается общая рекуррентная схема для решения этой задачи.