В этом разделе мы предложим метод построения решения игры
В этом разделе мы предложим метод построения решения игры ![]() ,
который приведет также к построению соответствующего оптимального пути.
,
который приведет также к построению соответствующего оптимального пути.
Решение игры ![]() строим методом обратной индукции,
двигаясь от окончательных позиций к начальной. Процедура поиска решения игры
строим методом обратной индукции,
двигаясь от окончательных позиций к начальной. Процедура поиска решения игры
![]() напоминает схему построения равновесия по
Нэшу в обычной позиционной игре. Существующие различия заключаются в следующем.
Предположим, что поддерево
напоминает схему построения равновесия по
Нэшу в обычной позиционной игре. Существующие различия заключаются в следующем.
Предположим, что поддерево ![]() принадлежит области кооперативного
поведения игрока
принадлежит области кооперативного
поведения игрока ![]() .
Как указывалось выше, кооперативная функция
.
Как указывалось выше, кооперативная функция ![]() определяет для каждой
позиции некоторую коалиционную структуру.
Тогда на множестве окончательных позиций поддерева
определяет для каждой
позиции некоторую коалиционную структуру.
Тогда на множестве окончательных позиций поддерева ![]() вместо выигрышей игрока
вместо выигрышей игрока ![]() необходимо рассматривать выигрыши коалиций,
включающих игрока
необходимо рассматривать выигрыши коалиций,
включающих игрока ![]() . На поддереве
. На поддереве ![]() , используя схему Нэша,
решение игрока
, используя схему Нэша,
решение игрока ![]() , максимизирующего выигрыш коалиции, к которой он
принадлежит, может быть легко определено. Однако, поскольку выигрыш игрока
, максимизирующего выигрыш коалиции, к которой он
принадлежит, может быть легко определено. Однако, поскольку выигрыш игрока
![]() не выделен из коалиционного выигрыша, при определении решений игрока
не выделен из коалиционного выигрыша, при определении решений игрока
![]() в его личных позициях, находящихся между позицией
в его личных позициях, находящихся между позицией ![]() и начальной позицией
и начальной позицией ![]() ,
где игрок
,
где игрок ![]() играет индивидуально, возникают трудности.
Если доля игрока
играет индивидуально, возникают трудности.
Если доля игрока ![]() в коалиционном выигрыше известна, то, применяя снова
схему Нэша, мы можем найти решения игрока
в коалиционном выигрыше известна, то, применяя снова
схему Нэша, мы можем найти решения игрока ![]() в его личных позициях
вдоль пути
в его личных позициях
вдоль пути
![]() .
Таким образом, определение изменений
выигрыша при переходе игрока с кооперативного поведения на
индивидуальное является главной проблемой, рассматриваемой в предлагаемом
алгоритме.
.
Таким образом, определение изменений
выигрыша при переходе игрока с кооперативного поведения на
индивидуальное является главной проблемой, рассматриваемой в предлагаемом
алгоритме.
В дальнейшем мы будем использовать следующие
обозначения. Пусть ![]() - некоторая позиция.
Обозначим через
- некоторая позиция.
Обозначим через ![]() множество позиций, непосредственно следующих за
множество позиций, непосредственно следующих за ![]() .
Обозначим игрока, принимающего решение в позиции
.
Обозначим игрока, принимающего решение в позиции ![]() ,
, ![]() , в игре
, в игре
![]() через
через ![]() . Будем говорить, что решение игрока
. Будем говорить, что решение игрока ![]() в позиции
в позиции ![]() ведет в позицию
ведет в позицию
![]() .
Введем вспомогательную функцию
.
Введем вспомогательную функцию ![]() , определяемую с помощью кооперативной
функции
, определяемую с помощью кооперативной
функции
![]() :
:
![\begin{displaymath}
c_f(x)=\left\{
\begin{array}{rl}
1,&\ \ \mbox{ если \ \ $f_{...
...x]
0,&\ \ \mbox{ если \ \ $f_{i(x)}(x)=0$.}
\end{array}\right.
\end{displaymath}](img103.gif) |
(2.1) |
Предположим, что длина игры ![]() составляет
составляет ![]() позицию.
Рассмотрим разбиение множества всех позиций дерева игры
позицию.
Рассмотрим разбиение множества всех позиций дерева игры ![]() на
на ![]() множеств
множеств ![]() ,
,
![]() , где множество
, где множество ![]() состоит из позиций достигаемых из начальной позиции
состоит из позиций достигаемых из начальной позиции ![]() за
за ![]() ходов.
Обозначим множество позиций, принадлежащих множеству
ходов.
Обозначим множество позиций, принадлежащих множеству ![]() , через
, через
![]() ,
, ![]() .
.
Начальный шаг.
Рассмотрим множество окончательных позиций ![]() .
Коалиционная структура в позиции
.
Коалиционная структура в позиции ![]() совпадает с коалиционной структурой в позиции
совпадает с коалиционной структурой в позиции ![]() ,
, ![]() .
Согласно кооперативной функции
.
Согласно кооперативной функции ![]() , в позиции
, в позиции ![]() формируются коалиции
формируются коалиции
![]() ,
,
![]() .
Выигрыш игрока
.
Выигрыш игрока ![]() в позиции
в позиции ![]() равен
равен
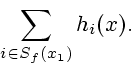 |
(2.2) |
Шаг 1.
Перейдем из окончательных позиций ![]() ,
, ![]() , к
предшествующим. Рассмотрим окончательную позицию
, к
предшествующим. Рассмотрим окончательную позицию ![]() .
Предположим, что
.
Предположим, что ![]() .
Тогда игрок
.
Тогда игрок ![]() кооперируется, и
в позиции
кооперируется, и
в позиции ![]() делает ход игрок
делает ход игрок
![]() ,
,
![]() .
Мы предписываем игроку
.
Мы предписываем игроку ![]() выбрать позицию
выбрать позицию
![]() из условия
из условия
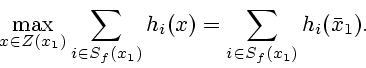 |
(2.3) |
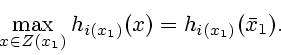 |
(2.4) |
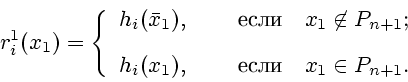 |
(2.5) |
Шаг 2.
Продолжим движение по направлению к корню дерева игры.
Найдем решения игроков
![]() в позициях
в позициях ![]() . Если на множестве
. Если на множестве ![]() известны выигрыши каждого игрока
известны выигрыши каждого игрока
![]() ,
, ![]() ,
то мы можем построить путь игры на поддеревьях
,
то мы можем построить путь игры на поддеревьях ![]() ,
,
![]() .
.
Рассмотрим множество
| (2.6) |
| (2.7) |
| (2.8) |
В качестве примера, подтверждающего существование непустого множества
![]() ,
предположим, что игрок
,
предположим, что игрок ![]() делает ход в поддереве
делает ход в поддереве ![]() дважды, т.е. существует позиция
дважды, т.е. существует позиция ![]() такая, что
такая, что
![]() и
и ![]() есть один и тот же игрок.
Допустим, что
есть один и тот же игрок.
Допустим, что ![]() и
и ![]() .
Тогда игрок
.
Тогда игрок ![]() принадлежит коалиции
принадлежит коалиции ![]() на поддереве
на поддереве ![]() и играет индивидуально в позиции
и играет индивидуально в позиции ![]() .
Поскольку выигрыш игрока
.
Поскольку выигрыш игрока ![]() не выделен из выигрыша
не выделен из выигрыша
![]() коалиции
коалиции ![]() , то
его выигрыш в позиции
, то
его выигрыш в позиции ![]() не известен.
не известен.
В общем случае отсутствие информации о выигрыше происходит в позициях,
где изменяется коалиционная структура, и это изменение касается текущего
игрока, принимающего решение. Для каждой позиции ![]() мы рассмотрим
два основных случая.
мы рассмотрим
два основных случая.
1) Предположим, что
![]() .
Пусть
.
Пусть ![]() .
Следовательно, в позиции
.
Следовательно, в позиции ![]() принимает решение игрок
принимает решение игрок
![]() .
Мы предписываем игроку
.
Мы предписываем игроку ![]() выбрать позицию
выбрать позицию
![]() из условия
из условия
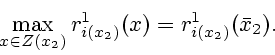 |
(2.9) |
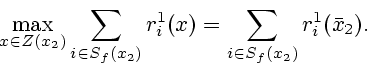 |
(2.10) |
2) Предположим, что
![]() .
Как выше указывалось, возникает неопределенность с выигрышами коалиции
.
Как выше указывалось, возникает неопределенность с выигрышами коалиции
![]() при
при ![]() и коалиции
и коалиции
![]() при
при ![]() .
Чтобы построить путь игры на поддереве
.
Чтобы построить путь игры на поддереве ![]() ,
необходимо найти некоторый дележ выигрыша коалиции
,
необходимо найти некоторый дележ выигрыша коалиции ![]() для каждой позиции
для каждой позиции ![]() .
Определим требуемый дележ, рассматривая вспомогательную
кооперативную игру
.
Определим требуемый дележ, рассматривая вспомогательную
кооперативную игру
![]() на поддереве
на поддереве ![]() с множеством игроков
с множеством игроков ![]() и х. ф.
и х. ф. ![]() ,
,
![]() , для каждой позиции
, для каждой позиции ![]() .
.
Для связности изложения детальное объяснение построения
х. ф. ![]() приводится ниже.
Сейчас же будем предполагать лишь, что х. ф.
приводится ниже.
Сейчас же будем предполагать лишь, что х. ф. ![]() известна.
известна.
Выигрыш наибольшей коалиции в кооперативной игре
![]() равен
равен
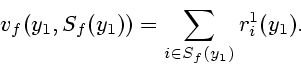 |
(2.11) |
| (2.12) |
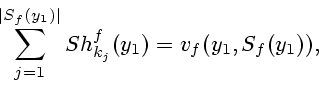 |
(2.13) |
 |
(2.14) |
Предположим, что ![]() .
Тогда для игрока
.
Тогда для игрока
![]() является оптимальным
реализация пути, проходящего через позицию
является оптимальным
реализация пути, проходящего через позицию
![]() ,
которая удовлетворяет условию:
,
которая удовлетворяет условию:
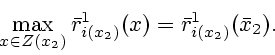 |
(2.15) |
Теперь пусть ![]() .
Так как игрок
.
Так как игрок ![]() кооперируется, то в позиции
кооперируется, то в позиции ![]() совершает ход
коалиция
совершает ход
коалиция
![]() .
Мы предписываем ей выбрать позицию
.
Мы предписываем ей выбрать позицию ![]() ,
удовлетворяющую условию:
,
удовлетворяющую условию:
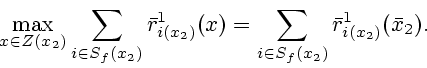 |
(2.16) |
Таким образом, путь на каждом поддереве ![]() ,
, ![]() , построен.
Отсюда, чтобы построить путь игры на поддеревьях
, построен.
Отсюда, чтобы построить путь игры на поддеревьях ![]() ,
, ![]() ,
достаточно определить решения игроков
,
достаточно определить решения игроков
![]() ,
, ![]() .
Зададим на множестве
.
Зададим на множестве ![]() функции
функции
![]() ,
, ![]() ,
такие, что для
,
такие, что для ![]() и
и ![]()
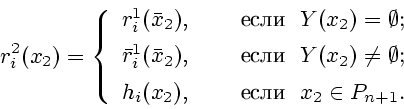 |
(2.17) |
Дальнейшие шаги процедуры аналогичны шагу 1 и 2. Опуская изложение
каждого шага, рассмотрим шаг ![]() .
Предположим, что продолжая двигаться к корню
.
Предположим, что продолжая двигаться к корню ![]() дерева игры, мы достигли позиций
дерева игры, мы достигли позиций ![]() .
Пусть функции
.
Пусть функции
![]() ,
, ![]() ,
определяют, какие выигрыши получают игроки
,
определяют, какие выигрыши получают игроки ![]() после выполнения игроками
после выполнения игроками
![]() ,
,
![]() ,
предписанных нами решений.
,
предписанных нами решений.
Шаг t.
Мы не будем затрагивать окончательные позиции из множества
![]() ,
потому что они могут быть рассмотрены точно так же, как в разделе 3.2.
Определим решения игроков
,
потому что они могут быть рассмотрены точно так же, как в разделе 3.2.
Определим решения игроков ![]() в промежуточных позициях
в промежуточных позициях
![]() .
Пусть
.
Пусть
| (2.18) |
| (2.19) |
| (2.20) |
1) Допустим, что
![]() для всех позиций
для всех позиций
![]() .
Согласно функциям
.
Согласно функциям ![]() ,
, ![]() ,
если решение игрока
,
если решение игрока ![]() приводит игру в позицию
приводит игру в позицию
![]() , то выигрыши, получаемые игроками
, то выигрыши, получаемые игроками ![]() в конце игры, будут равны
в конце игры, будут равны
![]() для игрока
для игрока ![]() и
и
![]() для игроков
для игроков ![]() ,
,
![]() ,
соответственно.
Если
,
соответственно.
Если ![]() , то в позиции
, то в позиции ![]() делает ход игрок
делает ход игрок
![]() и мы предпишем ему выбрать позицию
и мы предпишем ему выбрать позицию ![]() удовлетворяющую условию
удовлетворяющую условию
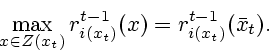 |
(2.21) |
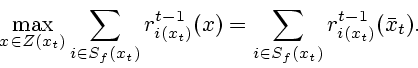 |
(2.22) |
2) Предположим, что для некоторой позиции ![]() множество
множество
![]() , состоящее из позиций,
для которых выигрыш игрока
, состоящее из позиций,
для которых выигрыш игрока
![]() не определен, не пусто.
не определен, не пусто.
Чтобы узнать решение игрока ![]() в позиции
в позиции ![]() ,
для каждой позиции
,
для каждой позиции
![]() рассмотрим кооперативную игру
рассмотрим кооперативную игру
![]()
![]() лиц с х. ф.
лиц с х. ф.
![]() ,
,
![]() .
Выигрыш наибольшей коалиции в этой кооперативной игре равен
.
Выигрыш наибольшей коалиции в этой кооперативной игре равен
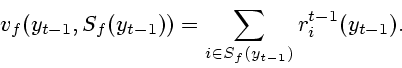 |
(2.23) |
| (2.24) |
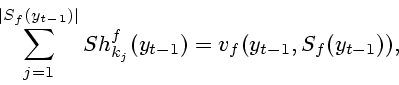 |
(2.25) |
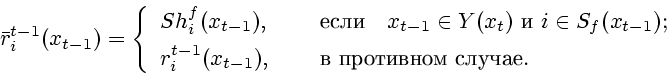 |
(2.26) |
Если ![]() , мы предписываем игроку
, мы предписываем игроку
![]() выбрать позицию
выбрать позицию
![]() из условия
из условия
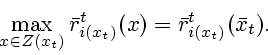 |
(2.27) |
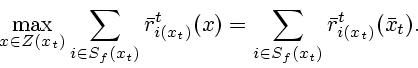 |
(2.28) |
В итоге, так как решения игроков ![]() были определены
для каждой позиции
были определены
для каждой позиции ![]() , развитие игры
, развитие игры ![]() на каждом поддереве
на каждом поддереве ![]() ,
, ![]() , найдено.
Кроме этого, на шаге
, найдено.
Кроме этого, на шаге ![]() процедуры были построены функции
процедуры были построены функции
![]() , определяющие, какой выигрыш получат
игроки
, определяющие, какой выигрыш получат
игроки ![]() после принятия игроками
после принятия игроками ![]() в позициях
в позициях
![]() предписанных нами решений.
Для
предписанных нами решений.
Для ![]() и
и ![]() функция
функция ![]() задается следующим
образом:
задается следующим
образом:
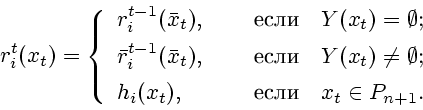 |
(2.29) |
Продолжая спускаться по дереву игры ![]() к начальной позиции
к начальной позиции ![]() и последовательно определяя решения игроков
и последовательно определяя решения игроков ![]() на оставшихся
множествах
на оставшихся
множествах ![]() ,
,
![]() ,
мы построим путь, который реализуется в игре
,
мы построим путь, который реализуется в игре ![]() при задании кооперативной функции
при задании кооперативной функции
![]() .
Мы будем называть данный путь оптимальным путем
частично-кооперативной игры
.
Мы будем называть данный путь оптимальным путем
частично-кооперативной игры ![]() и
обозначать его через
и
обозначать его через ![]() .
.
Кооперативные игры
Обсудим построение кооперативных игр ![]() ,
, ![]() .
Укажем метод построения х. ф.
.
Укажем метод построения х. ф. ![]() ,
,
![]() , игры
, игры
![]() .
.
При построении оптимального пути развития игры ![]() в разделах 3.2-3.5 было определено поведение игроков
в разделах 3.2-3.5 было определено поведение игроков ![]() в каждой личной позиции принятия решения. Такое поведение,
как функция от текущих позиций, называется стратегией.
Обозначим через
в каждой личной позиции принятия решения. Такое поведение,
как функция от текущих позиций, называется стратегией.
Обозначим через
![]() набор стратегий, определенных в разделах 3.2-3.5, приводящий
к оптимальному пути
набор стратегий, определенных в разделах 3.2-3.5, приводящий
к оптимальному пути ![]() игры
игры ![]() .
Кооперативная игра
.
Кооперативная игра ![]() строится с помощью этих стратегий.
Рассмотрим след
строится с помощью этих стратегий.
Рассмотрим след
![]() набора
набора ![]() на поддереве
на поддереве ![]() .
Для игроков
.
Для игроков
![]() зафиксируем стратегии
зафиксируем стратегии
![]() и рассмотрим подыгру
и рассмотрим подыгру
![]() игры
игры ![]() ,
в которой выборы игроков
,
в которой выборы игроков
![]() в их личных позициях
зафиксированы в соответствии со стратегиями
в их личных позициях
зафиксированы в соответствии со стратегиями
![]() .
Таким образом, игра
.
Таким образом, игра
![]() есть игра между игроками из
коалиции
есть игра между игроками из
коалиции ![]() .
Для каждой подкоалиции
.
Для каждой подкоалиции
![]() рассмотрим ассоциированную
с
рассмотрим ассоциированную
с
![]() игру с нулевой суммой
игру с нулевой суммой
![]() между двумя игроками:
коалицией
между двумя игроками:
коалицией ![]() , являющейся максимизирующим игроком
(выигрыш коалиции
, являющейся максимизирующим игроком
(выигрыш коалиции ![]() равен сумме выигрышей игроков из
равен сумме выигрышей игроков из ![]() ),
и коалицией
),
и коалицией
![]() , являющейся минимизирующим
игроком (выигрыш коалиции
, являющейся минимизирующим
игроком (выигрыш коалиции
![]() равен выигрышу
коалиции
равен выигрышу
коалиции ![]() с обратным знаком).
Можно показать, что выигрыш каждой коалиции
с обратным знаком).
Можно показать, что выигрыш каждой коалиции ![]() ,
определенный таким образом, не может превысить величины
,
определенный таким образом, не может превысить величины
![]() ,
поскольку по построению коалиция
,
поскольку по построению коалиция ![]() получает
выигрыш
получает
выигрыш ![]() , используя наилучшие ответные
стратегии против стратегий
, используя наилучшие ответные
стратегии против стратегий
![]() игроков
игроков
![]() .
Пусть
.
Пусть ![]() будет значением игры
будет значением игры
![]() .
С помощью выигрышей
.
С помощью выигрышей ![]() ,
,
![]() , вектор Шепли
строится в игре
, вектор Шепли
строится в игре ![]() обычным способом.
обычным способом.