3. Значение игры $\Gamma_f(x_0)$

Согласно процедуре, предложенной в разделе 3, мы получили выигрыши игроков $i\in N$, соответствующие оптимальному пути $x(f)$. Эти выигрыши определяются как $r^T_i(x_0)$, $i\in N$. Мы будем называть вектор $r(x_0)=(r^T_1(x_0),\ldots,r^T_n(x_0))$ значением частично-кооперативной игры.

П р и м е р 2. Рассмотрим позиционную игру $\Gamma$ с деревом игры $K(x_0)$, изображенным на рис. 2.

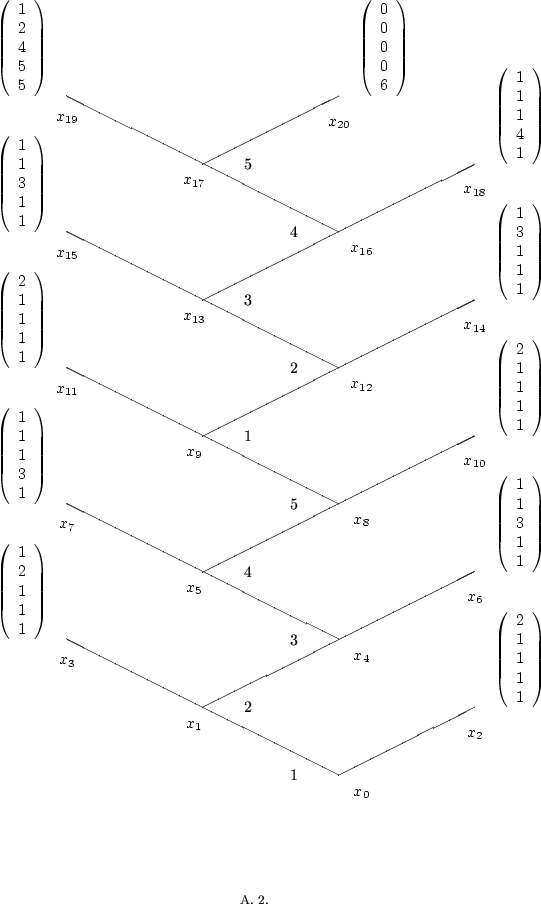
Здесь $N=\{1,2,3,4,5\}$. Личные позиции игрока $1$ - позиции $x_0$ и $x_9$, игрока $2$ - $x_1$ и $x_{12}$, игрока $3$ - $x_4$ и $x_{13}$, игрока $4$ - $x_5$ и $x_{16}$, и игрока $5$ - $x_8$ и $x_{17}$. Выигрыши записаны в окончательных позициях, причем в каждом столбце верхнее число есть выигрыш игрока $1$ и т.д. Предположим, что кооперативная функция $f=(f_1,\ldots,f_5)$ имеет следующую форму: $f_1(x_0)=0$, $f_1(x_9)=1$, $f_2(x_1)=0$, $f_2(x_{12})=1$, $f_3(x_4)=0$, $f_3(x_{13})=0$, $f_4(x_5)=0$, $f_4(x_{16})=0$, $f_5(x_8)=0$, $f_5(x_{17})=1$. Тогда множество игроков в игре $\Gamma_f(x_0)$ есть $N_f=\Bigl\{1,2,3,4,5,\{1,2,5\}\Bigr\}$. В $\Gamma_f(x_0)$ игрок $1$ принимает решение в позиции $x_0$, игрок $2$ - в $x_1$, игрок  $3$ - в $x_4$ и $x_{13}$, игрок  $4$ - в $x_5$ и $x_{16}$, игрок $\{1,2,5\}$ - в $x_9$, $x_{12}$ и $x_{17}$. Выигрыши игрока $\{1,2,5\}\in N_f$ в $\Gamma_f(x_0)$ задаются суммой соответствующих терминальных выигрышей игроков $1$, $2$ и $5$ в игре $\Gamma$.

Построим оптимальный путь частично-кооперативной игры $\Gamma_f(x_0)$.
Процедура построения оптимального пути начинается в окончательных позициях $x_{19}$ и $x_{20}$. Коалиционная структура в $x_{19}$ и $x_{20}$ та же, что и в $x_{17}$, т.е. $S_f(x_{17})=\{1,2,5\}$, $\{3\}$ и $\{4\}$. Тогда выигрыши для игроков из $N_f$ в позициях $x_{19}$ и $x_{20}$ задаются в виде троек $(8,4,5)$ и $(6,0,0)$ соответственно, причем первая компонента есть выигрыш игрока $\{1,2,5\}$, вторая - игрока 3, и третья - игрока  4. В позиции $x_{17}$ игрок $\{1,2,5\}$ делает ход налево, чтобы получить $1+2+5=8$. Тогда $r^1(x_{17})=(1,2,4,5,5)^*$ (знак * обозначает транспонирование) и $r^1(x_{18})=(1,1,1,4,1)^*$. Так как $r^1_4(x_{17})>r^1_4(x_{18})$, то в позиции $x_{16}$ для игрока 4 оптимальным является ход налево, чтобы получить $5$ в $x_{19}$. Тогда $r^2(x_{15})=(1,1,3,1,1)^*$, $r^2(x_{16})=(1,2,4,5,5)^*$. Так как $r^2_3(x_{15})<r^2_3(x_{16})$, то в позиции $x_{13}$ для игрока $3$ оптимальным является ход направо, чтобы получить $4$ в $x_{19}$. Тогда $r^3(x_{13})=(1,2,4,5,5)^*$, $r^3(x_{14})=(1,3,1,1,1)^*$. В $x_{12}$ ходит игрок $\{1,2,5\}$. Для него оптимальным является ход налево, чтобы получить $r^3_1(x_{13})+r^3_2(x_{13})+r^2_5(x_{13})=8$. Тогда $r^4(x_{12})=(1,2,4,5,5)^*$, $r^4(x_{11})=(2,1,1,1,1)^*$. В $x_9$ решение принимает снова игрок $\{1,2,5\}$. Для него оптимальным является ход направо, чтобы получить $r^4_1(x_{12})+r^4_2(x_{12})+r^4_5(x_{12})=8$ в $x_{19}$.

В позиции $x_8$ игрок 5 не принадлежит коалиции $\{1,2,5\}$ и играет индивидуально. Однако его доля в предполагаемом выигрыше коалиции $\{1,2,5\}$ не определена. Построим на поддереве $K(x_9)$ с начальной позицией $x_9$ кооперативную игру $G_f\Bigl(x_9,S_f(x_9)\Bigr)$, $S_f(x_9)=\{1,2,5\}$. Фиксируя определенные выше решения игрока $3$ в $x_{13}$ и игрока $4$ в $x_{16}$, мы можем построить х. ф. $v_f(x_9, R)$, $R\subset \{1,2,5\}$. Х. ф. $v_f(x_9, R)$ имеет следующие значения: $v_f(x_9,\{1,2,5\})=8$, $v_f(x_9,\{1,2\})=4$, $v_f(x_9,\{2,5\})=2$, $v_f(x_9,\{1,5\})=3$, $v_f(x_9,\{1\})=2$, $v_f(x_9,\{2\})=1$, $v_f(x_9,\{5\})=1$. Отсюда, вектор Шепли $Sh^f(x_9)=\Bigr(Sh^f_1(x_9),Sh^f_2(x_9),Sh^f_5(x_9)\Bigl)$ равен $(3\frac{1}{2},2\frac{1}{2},2)$. Тогда $r^5(x_9)=(3\frac{1}{2},2\frac{1}{2},4,5,2)^*$, $r^5(x_9)=(2,1,1,1,1)^*$. В позиции $x_8$ для игрока 5 оптимальным является ход налево, чтобы получить коалиционную долю $2$ в $x_{19}$. Тогда $r^6(x_8)=(3\frac{1}{2},2\frac{1}{2},4,5,2)^*$, $r^6(x_7)=(1,1,1,3,1)^*$. Сравнивая $r^6_4(x_8)$ и $r^6_4(x_7)$, получаем, что в позиции $x_5$ для игрока 4 лучше идти направо. Тогда $r^7(x_5)=(3\frac{1}{2},2\frac{1}{2},4,5,2)^*$, $r^7(x_6)=(1,1,3,1,1)^*$. Игроку 3 следует идти налево в $x_{4}$, чтобы получить 4. Тогда $r^8(x_4)=(3\frac{1}{2},2\frac{1}{2},4,5,2)^*$, $r^8(x_3)=(1,2,1,1,1)^*$. В соответствии с заданной кооперативной функцией $f$ игрок 2 не кооперируется в позиции $x_1$. Его доля в выигрыше коалиции $\{1,2,5\}$ определяется согласно вектору Шепли кооперативной игры $G_f\Bigl(x_9,S_f(x_9)\Bigr)$. Максимизируя собственный выигрыш, в $x_1$ игрок 2 должен идти направо. Тогда $r^9(x_1)=(3\frac{1}{2},2\frac{1}{2},4,5,2)^*$, $r^9(x_2)=(2,1,1,1,1)^*$. Игрок 1 не кооперируется в позиции $x_0$. Его доля в предполагаемом выигрыше коалиции $\{1,2,5\}$ равна $r^9_1(x_1)=3\frac{1}{2}$. Отсюда в $x_0$ игроку 1 следует идти налево и $r^{10}(x_0)=(3\frac{1}{2},2\frac{1}{2},4,5,2)^*$. В итоге в игре $\Gamma_f(x_0)$ оптимальным путем является

$$x(f)=\{x_0,x_1,x_4,x_5,x_8,x_9,x_{12},x_{13},x_{16},x_{17},x_{19}\},$$ (3.1)

а значение игры равно

$$r(x_0)=(3.5,2.5,4,5,2).$$ (3.2)

З а м е ч а н и е 3. Рассмотрим обычную кооперативную игру $G(x_0)$, построенную на том же самом дереве $K(x_0)$ из рис. 2. Заметим, что путь $x^*=\{x_0,\ldots,x_{19}\}$, приводящий к наибольшему общему выигрышу в игре $G(x_0)$, совпадает с оптимальным путем $x(f)$ игры $\Gamma_f(x_0)$. Таким образом, кооперация игроков $1$, $2$ и $5$ на поддереве $K(x_9)$ достаточна для того, чтобы путь $x^*$ был бы реализован. Очевидно, что выигрыши игроков согласно значению $r(x_0)$ игры $\Gamma_f(x_0)$ и оптимальному в некотором смысле дележу игры $G(x_0)$ совершенно различны. Рассмотрим вектор Шепли $Sh(x_0)=(4\frac{1}{3},3\frac{1}{3},3\frac{1}{3},3,3)$ игры $G(x_0)$. Сравнивая компоненты игроков 3 и 4 в $r(x_0)$ и $Sh(x_0)$, можно заметить, что игроки 3 и 4 теряют в выигрыше в случае, если они кооперируются.

Изменяя кооперативную функцию $f$, получаем класс $\Gamma_F(x_0)$ всех частично-кооперативных игр $\Gamma_f(x_0)$, которые могут быть определены на дереве $K(x_0)$. Представляется, что дележ наибольшего общего выигрыша в обычной кооперативной игре был бы более справедливым, если бы он строился с помощью значений $r(x_0)$ игр $\Gamma_f(x_0)\in \Gamma_F(x_0)$.

Поступила 17.06.99