1. Основная модель

Пусть $\Gamma$ - динамическая позиционная игра $n$ лиц с полной информацией. Обозначим множество игроков через $N=\{1,\ldots,n\}$. Пусть $K(x_0)$ есть дерево игры с начальной позицией $x_0$. Согласно определению позиционной игры, на $K(x_0)$ задано разбиение множества позиций на $n+1$ множество $P_1,\ldots,P_n,P_{n+1}$, где $P_i$ - множество личных позиций игрока $i$, а $P_{n+1}$ - множество окончательных позиций. Выигрыши игроков в $\Gamma$ определяются вещественнозначными функциями $h_i\colon P_{n+1}\to R^1_+$, $i\in N$.

Под частично-кооперативным поведением игрока будем понимать такое поведение, при котором игрок может как кооперироваться, так и играть индивидуально. Игрока, принимающего решение в позиции $x$ (делающего ход, т.е. передвигающего "движущуюся точку" из позиции $x$ в альтернативную позицию), будем обозначать $i(x)$ (так что $x\in P_{i(x)}$). Изменим позиционную игру $\Gamma$, предполагая, что игроки могут кооперироваться при определенных условиях. Трансформированную игру назовем игрой с частичной кооперацией или частично-кооперативной игрой и будем обозначать ее снова через $\Gamma$. В этом разделе описываются правила частичной кооперации.

О п р е д е л е н и е. Пусть $i\in N$. Функция $f_i\colon P_i\to \{0,1\}$ называется кооперативной функцией игрока $i$, если для любого пути $\{x_0,\ldots,x',x'',\ldots,\bar x\}$, где $x'\in P_i$ и $\bar x\in P_{n+1}$, из условия $f_i(x')=1$ следует, что для всех позиций $y\in P_i\cap\{x'',\ldots,\bar x\}$, если они существуют, $f_i(y)=1$.

Вектор-функция $f=(f_1,\ldots,f_n)$ называется кооперативной функцией игры.

Кооперативная функция позволяет указать коалицию $C(x)$ в каждой позиции $x$:

$$C(x)=\left\{ \begin{array}{ll} S_f(x),&\quad\mbox{ если $f_i... ... [1ex] \{i\},&\quad\mbox{ если $f_i(x)=0$,} \end{array}\right.$$ (1.1)

где

$$S_f(x)=S^1_f(x)\cup S^2_f(x),$$

$$S^1_f(x)=\Bigl\{ j\in N \Bigl\vert P_j\cap K(x)=\emptyset\ \... ...\ \exists y\in P_j\cap\{x_0,\ldots,x\}\colon f_j(y)=1 \Bigr\},$$ (1.2)

$$S^2_f(x)=\Bigl\{j\in N\setminus S^1_f(x)\Bigl\vert f_j(y)=1\, \forall y\in P_j\cap K(x) \Bigr\}.$$ (1.3)

Множество $S^1_f(x)$ состоит из игроков, которые проявили кооперативную активность вдоль пути ведущего в $x$ и не принимают решений в ходе последующего развития игры на поддереве $K(x)$ с начальной позицией $x$. Исходя из определения кооперативной функции, игроков, принадлежащих $S^1_f(x)$, следует считать кооперирующимися на всем поддереве $K(x)$.

Множество $S^2_f(x)$ включает игроков, которые кооперируются во всех своих личных позициях поддерева $K(x)$. Говоря, что игрок $i\in N$ придерживается кооперативного поведения в позиции $x\in K(x_0)$, мы будем иметь в виду, что в позиции $x$ игрок $i$ принимает решение, исходя из интересов коалиции (т.е. стремясь к максимальному суммарному выигрышу игроков $i\in C(x)$). Игроки из множества $N \setminus S_f(x)$ рассматриваются в позиции $x$ как индивидуальные игроки. Поскольку $S_f(x)$ определяется кооперативной функцией $f$, вся коалиционная структура в позиции $x$

$$S_f(x),\ \{j_1\},\ \{j_2\},\ldots,\{j_{ \vert N \setminus S_f(x) \vert }\}$$ (1.4)

также формируется в зависимости от $f$.

Определим позиционную игру $\Gamma_f(x_0)$. Игра $\Gamma_f(x_0)$ создается на основе частично-кооперативной игры $\Gamma$ с использованием кооперативной функции $f$. Дерево игры $\Gamma_f(x_0)$ совпадает с деревом $K(x_0)$ игры $\Gamma$. Множество ${\cal N}_f$ участников игры $\Gamma_f(x_0)$ формируется с учетом кооперативной функции $f$ и состоит из подмножеств множества $N$ игроков игры $\Gamma$:

$${\cal N}_f=\{C\subset N:\ \exists x\in K(x_0),C(x)=C\}.$$

Множество (коалиция) $C\in{\cal N}_f$ будет рассматриваться в качестве
участника игры (игрока) в позиционной игре $\Gamma_f(x_0)$, принимающего решение в позициях $x\in W(C)$, где

$$W(C)=\Bigl\{x\in K(x_0):\ C(x)=C\Bigr\}.$$

Выигрыш игрока $C\in{\cal N}_f$ игры $\Gamma_f(x_0)$ определяется на множестве окончательных позиций дерева игры $K(x_0)$ как сумма выигрышей игроков $i\in C$ игры $\Gamma$:

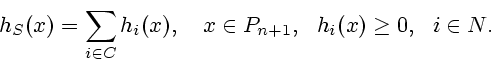$$h_S(x)=\sum_{i\in C}h_i(x),\quad x\in P_{n+1}, \ \ h_i(x)\ge 0,\ \ i\in N.$$ (1.5)

Может случиться так, что каждое множество $C\in{\cal N}_f$ будет состоять только из одного игрока. Такая игра имеет место, если для любой позиции $x$ дерева игры $K(x_0)$ множество $S_f(x)$ одноэлементно или пусто. Как противоположный случай, $\Gamma_f(x_0)$ может быть игрой с одним игроком (множество ${\cal N}_f$ состоит только из игрока $N$). Это произойдет, если $C(x)=N$ для всех позиций $x\in P_i$, $i\in N$. В наиболее сложном случае множество ${\cal N}_f$ может состоять из всех подмножеств множества $N$.

Рис. 1.

П р и м е р 1. Рассмотрим позиционную игру $\Gamma$ с деревом игры, изображенным на рис. 1, где $N=\{1,2,3\}$. Личные позиции игрока 1 - позиции $x_0$ и $x_{22}$, игрока 2 - $x_{11}$ и $x_{23}$, игрока 3 - $x_{21}$ и $x_{12}$. Выигрыши игроков записаны в окончательных позициях. Предположим, что кооперативная функция $f=(f_1,f_2,f_3)$ имеет следующую форму: $f_1(x_0)=0$, $f_1(x_{22})=0$, $f_2(x_{11})=1$, $f_2(x_{23})=0$, $f_3(x_{21})=1$, $f_3(x_{12})=0$.

Построим игру $\Gamma_f(x_0)$. Определим коалиционную структуру в позиции $x_{11}\in P_2$. Поскольку игрок 1 не кооперируется в $x_0$ и имеет личную позицию в поддереве $K(x_{11})$, множество $S^1_f(x_{11})$ пусто. Так как $f_3(x_{21})=1$, $f_2(x_{11})=1$, и $f_1(x_{22})=0$, в каждой своей личной позиции на поддереве $K(x_{11})$ кооперируются только игроки $2$ и $3$. Поэтому $S^2_f(x_{11})=\{2,3\}$. В результате $S_f(x_{11})=\{2,3\}$, а коалиционная структура в позиции $x_{11}$ есть $\{2,3\}$, $\{1\}$.

Действуя аналогичным способом, можно установить, что $S_f(x_{21})=\{2,3\}$. Тогда, $i_f(x_0)=\{1\}$, $i_f(x_{11})=\{2,3\}$, $i_f(x_{12})=\{3\}$, $i_f(x_{21})=\{2,3\}$, $i_f(x_{22})=\{1\}$, $i_f(x_{23})=\{2\}$. Таким образом, ${\cal N}_f=\Bigl\{1,2,3,\{2,3\}\Bigr\}$.

Игрок $\{2,3\}\in{\cal N}_f$ имеет следущие выигрыши: $h_{\{2,3\}}(x_{31})=3$,
$h_{\{2,3\}}(x_{32})=5$, $h_{\{2,3\}}(x_{33})=5$, $h_{\{2,3\}}(x_{34})=3$, $h_{\{2,3\}}(x_{35})=4$, $h_{\{2,3\}}(x_{36})=5$, $h_{\{2,3\}}(x_{24})=3$.

Выигрыши игроков $i\in N$ в игре $\Gamma_f(x_0)$ совпадают с их выигрышами в игре $\Gamma$.

З а м е ч а н и е 1. Возможен случай, когда игрок, несмотря на то, что он находится в позиции своего кооперативного поведения, играет индивидуально. Изменим кооперативную функцию игрока 1 в примере 1. Пусть $f_1(x_{0})=1$, $f_1(x_{22})=1$. Рассмотрим множество $S_f(x_0)$. Хотя игроки 2 и 3 кооперируются в каждой своей личной позиции на поддереве $K(x_{11})$, так как $f_2(x_{23})=f_3(x_{12})=0$, множество $S_f(x_0)$ состоит только из игрока $1$. Поэтому можно утверждать, что игрок 1 принимает решение в позиции $x_0$ как индивидуальный игрок.

З а м е ч а н и е 2. Для произвольной позиции $x$ и позиции $y$, непосредственно предшествующей $x$, допустим, что множество $S_f(y)$ не пусто. Тогда, $S_f(x)$ также не пусто, и более того, имеет место включение $S_f(y)\subset S_f(x)$.

Одним из способов получения решения позиционной игры $\Gamma_f(x_0)$ является построение равновесия по Нэшу. Выигрыши каждого игрока $C\in{\cal N}_f$ в игре $\Gamma_f(x_0)$ будут определяться в соответствии с равновесием по Нэшу (которое, конечно, может быть не единственным, однако всегда существует, поскольку $\Gamma$ - игра с полной информацией). Таким образом, мы можем построить функцию $\Phi(C)$, $C\in{\cal N}_f$, определяющую выигрыш каждой коалиции, создаваемой в игре $\Gamma$ в соответствии с кооперативной функцией $f$. Данная функция может рассматриваться как аналог характеристической функции (х.ф.) из теории кооперативных игр. Однако остается не ясным, каким образом с помощью $\Phi(C)$ можно построить оптимальный в некотором смысле дележ $\alpha=(\alpha_1,\ldots,\alpha_n)$, компоненты которого рассматривались бы как выигрыши индивидуальных игроков $i\in N$ в частично-кооперативной игре $\Gamma$. Указанная проблема является темой отдельного исследования и в данной работе обсуждаться не будет.

Для нахождения подходящего решения частично-кооперативной игры воспользуемся другим подходом, основанным на применении как равновесия по Нэшу, так и решений из кооперативной теории игр. При построении такого решения мы будем действовать методом обратной индукции, шаг за шагом находя оптимальное поведение игроков. Мы будем называть данную процедуру алгоритмом построения оптимальногo пути.