В работе изучается следующая задача гарантированного поиска. Команда преследователей пытается поймать ``невидимого" для них убегающего на связном топологическом графе. Игроки обладают ``простыми движениями" с ограниченными максимальными скоростями, а топологический граф является фазовым ограничением для их траекторий. Задача заключается в нахождении наименьшего числа преследователей, необходимого для поимки убегающего при тех или иных условиях поиска.
Авторами первых статей, давших толчок к появлению многочисленных публикаций, посвященных задачам поиска на графах, являются Парсонс [18] и Петров [3]. С момента опубликования этих работ задачи поиска на графах привлекают внимание многих исследователей из разных областей математики по нескольким причинам. Первая причина - это связь некоторых задач поиска с играми в камни (pebble games) [13], которые имеют отношение к задачам рационального использования памяти ЭВМ. Во-вторых, выяснилось, что некоторые инварианты графов, первоначально возникшие в теории сверхбольших интегральных схем (СБИС), такие как ширина разреза [16], топологическая ширина ленты [15], величина вершинного разделения графа [9], во многих случаях имеют теоретико-игровую интерпретацию. Третьей причиной является связь задач поиска с путевой и древесной шириной графа - важнейшими параметрами в теории миноров графов, разработанной Робертсоном и Сеймуром [6,8]. Проблемы поиска на графах возникают также в задачах о координации движений роботов [19], в некоторых моделях борьбы с компьютерными вирусами [6] и в задачах сохранения секретности информации, передаваемой по электронным сетям с мобильными подслушивающими устройствами (``жучками") [12]. Подробную информацию о задачах поиска и их ``родственниках" можно найти в обзорах [6,10,17]. Некоторые результаты настоящей статьи опубликованы в [11].
Многие из полученных авторами результатов, нетрадиционных для ``российской" теории управления, встретили понимание и поддержку со стороны выдающегося представителя екатеринбургской математической школы Андрея Измаиловича Субботина, о чем мы, его петербургские коллеги, всегда будем помнить.
В дальнейшем под словом граф мы будем подразумевать
конечный связный топологический граф, вершины
которого ![]() суть точки в
суть точки в ![]() , а ребра
, а ребра
![]() - непересекающиеся
конечнозвенные ломаные с концами в соответствующих вершинах. Граф
предполагается не имеющим петель и кратных ребер.
- непересекающиеся
конечнозвенные ломаные с концами в соответствующих вершинах. Граф
предполагается не имеющим петель и кратных ребер.
На графе ![]() находятся
находятся ![]() преследователей
преследователей
![]() и убегающий
и убегающий ![]() .
Предполагается, что
преследователи и убегающий обладают в
.
Предполагается, что
преследователи и убегающий обладают в ![]() (граф вложен в
(граф вложен в ![]() ) простыми движениями:
) простыми движениями:
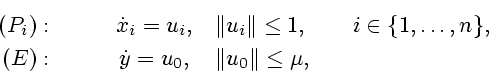
Обозначим через ![]() внутреннюю метрику графа
внутреннюю метрику графа ![]() , т.е.
, т.е.
![]() есть длина (в евклидовой метрике)
кратчайшего пути в
есть длина (в евклидовой метрике)
кратчайшего пути в ![]() с концами в
с концами в ![]() и
и ![]() , а через
, а через
![]() - неотрицательное число, характеризующее
``радиус поимки".
- неотрицательное число, характеризующее
``радиус поимки".
Убегающий ![]() считается пойманным преследователем
считается пойманным преследователем ![]() в
момент
в
момент ![]() , если
, если
![]() .
Совокупность траекторий преследователей
.
Совокупность траекторий преследователей
![]() ,
,
![]() называется
программой преследователей, заданной на промежутке
называется
программой преследователей, заданной на промежутке ![]() .
Программа
.
Программа ![]() преследователей
преследователей
![]() ,
заданная на
,
заданная на ![]() , называется выигрывающей, если для
любой траектории
убегающего
, называется выигрывающей, если для
любой траектории
убегающего ![]() , заданной на
, заданной на ![]() , существуют
, существуют ![]() и
и
![]() такие, что
такие, что
![]() , т.е. независимо от выбора
траектории убегающий ловится одним из преследователей.
Ставится вопрос о нахождении наименьшего натурального числа
, т.е. независимо от выбора
траектории убегающий ловится одним из преследователей.
Ставится вопрос о нахождении наименьшего натурального числа ![]() такого, что у
такого, что у ![]() преследователей существует выигрывающая
программа, заданная на некотором промежутке
преследователей существует выигрывающая
программа, заданная на некотором промежутке ![]() . Понятно,
что эта величина
зависит только от графа
. Понятно,
что эта величина
зависит только от графа ![]() , а также от чисел
, а также от чисел ![]() и
и ![]() . Будем обозначать ее че-
. Будем обозначать ее че-
рез
![]() .
.
Задачу поиска бывает удобно интерпретировать как задачу очистки
графа от ``распыленного" убегающего. Будем говорить, что для
программы
![]()
![]() ,
,
![]() ,
, ![]() , точка
, точка
![]() является загрязненной в момент времени
является загрязненной в момент времени
![]() , если найдется траектория
убегающего
, если найдется траектория
убегающего
![]() ,
, ![]() , такая, что
, такая, что ![]() , и для всякого
, и для всякого
![]() и
и
![]() имеет место неравенство
имеет место неравенство
![]() .
Множество загрязненных в момент
.
Множество загрязненных в момент ![]() точек графа
точек графа ![]() обозначим через
обозначим через
![]() .
Множество точек
.
Множество точек
![]() называется
очищенным в момент
называется
очищенным в момент ![]() множеством.
Очевидно, что программа
множеством.
Очевидно, что программа
![]() ,
, ![]() является выигрывающей тогда и только тогда, когда для некоторого
является выигрывающей тогда и только тогда, когда для некоторого
![]() весь граф
весь граф
![]() очищен.
очищен.
Случай ![]() (убегающий может двигаться сколь угодно
быстро) и
(убегающий может двигаться сколь угодно
быстро) и
![]() первоначально рассматривался Парсонсом
[18]. Отметим, что в этом случае наименьшее число
преследователей, необходимое для существования выигрывающей
программы, не зависит от длин ребер и является инвариантом,
зависящим только от комбинаторной схемы графа. Случай, когда
первоначально рассматривался Парсонсом
[18]. Отметим, что в этом случае наименьшее число
преследователей, необходимое для существования выигрывающей
программы, не зависит от длин ребер и является инвариантом,
зависящим только от комбинаторной схемы графа. Случай, когда ![]() и
и
![]() изучался Головачем [1], а
случай
изучался Головачем [1], а
случай ![]() и
и
![]() - Петровым [3]. Задачи
поиска Головача и Петрова являются естественным обобщением задачи
Парсонса. Зависимость от длин ребер значительно усложняет решение
задачи и определить величину
- Петровым [3]. Задачи
поиска Головача и Петрова являются естественным обобщением задачи
Парсонса. Зависимость от длин ребер значительно усложняет решение
задачи и определить величину
![]() можно лишь в исключительных случаях.
можно лишь в исключительных случаях.
Одним из основополагающих фактов в изучении задачи поиска
является теорема ЛаПо [14], гласящая, что в случае
![]() и
и
![]() the ``recontamination`` does not
help to search a graph.1 К сожалению, для более общих задач
поиска данный факт не верен и ``стандартная" техника неприменима.
the ``recontamination`` does not
help to search a graph.1 К сожалению, для более общих задач
поиска данный факт не верен и ``стандартная" техника неприменима.
Ранее в работах [1,2,4,5] авторами был получен ряд фундаментальных результатов о поиске. Основной целью данной работы является демонстрация того, как можно применять эти результаты при решении модельных задач.
В настоящей работе мы обозначаем
через ![]() ,
, ![]() ,
, ![]() графы, состоящие из всех ребер и вершин
тетраэдра, куба и октаэдра, соответственно.
Полный граф с
графы, состоящие из всех ребер и вершин
тетраэдра, куба и октаэдра, соответственно.
Полный граф с ![]() вершинами (т.е. граф, любые две вершины которого
смежны) обозначается через
вершинами (т.е. граф, любые две вершины которого
смежны) обозначается через ![]() . Заметим, что графы
. Заметим, что графы ![]() и
и ![]() изоморфны.
Мы полагаем, что в графах
изоморфны.
Мы полагаем, что в графах
![]() ,
, ![]() ,
, ![]() и
и ![]() все ребра имеют единичную длину.
все ребра имеют единичную длину.
Дальнейшая часть работы имеет следующую структуру. В §2
вычисляются числа
![]() ,
,
![]() ,
,
![]() и
и
![]() для всех
для всех
![]() . В §3
доказывается, что для всякого
. В §3
доказывается, что для всякого ![]()
![]() при
при
![]() . Далее находятся числа
. Далее находятся числа
![]() ,
,
![]() и
и
![]() при
при ![]() и доказывается,
что
и доказывается,
что
![]() при
при ![]() ,
,
![]() при
при
![]() и
и
![]() при
при
![]() .
В заключение (§4) мы формулируем некоторые
гипотезы о поисковых числах графов правильных многогранников.
.
В заключение (§4) мы формулируем некоторые
гипотезы о поисковых числах графов правильных многогранников.