3. Случай
Пусть ![]() - граф, все ребра которого имеют
единичную длину.
Заданная на
- граф, все ребра которого имеют
единичную длину.
Заданная на ![]() программа преследователей
программа преследователей ![]() называется дискретной, если
называется дискретной, если ![]() - натуральное
число и для всякого
- натуральное
число и для всякого
![]() на
протяжении
на
протяжении ![]() каждый из преследователей либо стоит в вершине графа,
либо переходит из вершины в смежную вершину с максимальной скоростью.
каждый из преследователей либо стоит в вершине графа,
либо переходит из вершины в смежную вершину с максимальной скоростью.
Следующее утверждение доказывается в работе [5].
Введем обозначения, необходимые для
дальнейших доказательств.
Пусть ![]() - один из графов
- один из графов
![]() ,
, ![]() .
Рассмотрим некоторую дискретную программу
.
Рассмотрим некоторую дискретную программу
![]() на
на ![]() при
при ![]() .
Легко убедиться, что во всякий целочисленный момент времени
.
Легко убедиться, что во всякий целочисленный момент времени
![]() внутренность всякого ребра (в топологии
внутренность всякого ребра (в топологии ![]() ) графа
) графа
![]() либо целиком очищена, либо целиком загрязнена.
либо целиком очищена, либо целиком загрязнена.
Обозначим через ![]() число преследователей, находящихся в
момент
число преследователей, находящихся в
момент ![]() в вершине
в вершине ![]() . Назовем вершину
. Назовем вершину ![]() особой в
момент
особой в
момент ![]() , если
, если ![]() не меньше числа загрязненных ребер,
инцидентных этой вершине. Будем обозначать через
не меньше числа загрязненных ребер,
инцидентных этой вершине. Будем обозначать через ![]() множество
всех особых вершин в момент
множество
всех особых вершин в момент ![]() , а через
, а через ![]() - его мощность.
Будем говорить, что вершина
- его мощность.
Будем говорить, что вершина ![]() является
является ![]() -особой в
момент
-особой в
момент ![]() , если
, если ![]() и
и ![]() . Назовем вершину
. Назовем вершину ![]() голой в момент
голой в момент ![]() , если все инцидентные ей ребра в этот
момент загрязнены. Будем обозначать через
, если все инцидентные ей ребра в этот
момент загрязнены. Будем обозначать через ![]() множество всех
голых вершин в момент
множество всех
голых вершин в момент ![]() , а через
, а через ![]() - его мощность.
Пусть
- его мощность.
Пусть ![]() - вершина степени
- вершина степени ![]() графа
графа ![]() . Тогда для всякой дискретной
программы
. Тогда для всякой дискретной
программы ![]() на
на ![]() легко доказываются следующие утверждения:
легко доказываются следующие утверждения:
Докажем теперь основную теорему, касающуюся полных графов.
Д о к а з а т е л ь с т в о. Заметим прежде всего, что ![]() преследователей достаточно
для поимки убегающего на
преследователей достаточно
для поимки убегающего на ![]() при любом
при любом ![]() . Для
доказательства неравенства
. Для
доказательства неравенства
![]() покажем, что
ни одна программа для
покажем, что
ни одна программа для ![]() преследователей не может быть
выигрывающей. Предположим противное, и пусть
преследователей не может быть
выигрывающей. Предположим противное, и пусть ![]() -
выигрывающая программа для
-
выигрывающая программа для ![]() преследователей. Сославшись на
теорему 9, мы можем предполагать, что
преследователей. Сославшись на
теорему 9, мы можем предполагать, что ![]() является
дискретной программой.
является
дискретной программой.
Покажем,
что при реализации ![]() все величины
все величины ![]() и,
следовательно, эта программа не может быть выигрывающей.
и,
следовательно, эта программа не может быть выигрывающей.
Рассмотрим три случая.
Случай 1. ![]() ,
,
![]() , т.е. в момент
, т.е. в момент ![]() особых вершин не
было,
а в момент
особых вершин не
было,
а в момент ![]() их стало
их стало
![]() .
.
Тогда в момент ![]() в неособых вершинах находятся
в неособых вершинах находятся
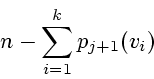
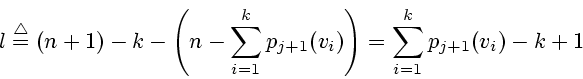
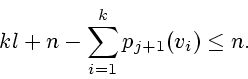
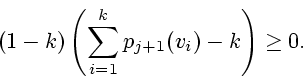
Так как по лемме 2
![]() для всех
для всех
![]() , то отсюда
следует,
что
, то отсюда
следует,
что
![]() . Таким образом, в случае 1 может возникнуть только одна особая
вершина.
. Таким образом, в случае 1 может возникнуть только одна особая
вершина.
Случай 2. В момент ![]() была одна особая вершина
была одна особая вершина ![]() ,
а в момент
,
а в момент ![]() особых вершин стало
особых вершин стало
![]() ,
, ![]() ,
(т.е. добавилось
,
(т.е. добавилось ![]() новых особых вершин).
новых особых вершин).
Тогда в неособых вершинах в момент ![]() находятся
находятся
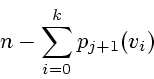
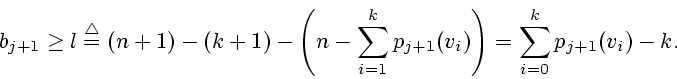
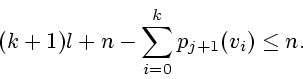
Это неравенство равносильно следующему
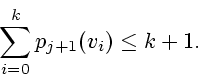
Случай 3. В момент ![]() была одна особая вершина
была одна особая вершина ![]() ,
а в момент
,
а в момент ![]() их стало
их стало
![]() ,
, ![]() ,
(т.е. вершина
,
(т.е. вершина ![]() стала неособой и
добавилось
стала неособой и
добавилось ![]() новых особых вершин).
Тогда в неособых вершинах в момент
новых особых вершин).
Тогда в неособых вершинах в момент ![]() находятся
находятся
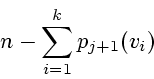
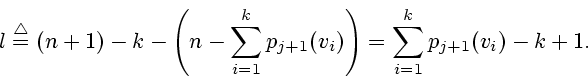
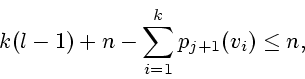
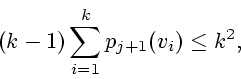
Ранее было отмечено, что в момент ![]() голых вершин не менее
голых вершин не менее ![]() .
С другой стороны, их не может быть более двух, так как в этом случае
в особой вершине было бы более двух преследователей. Отсюда следует, что
в момент
.
С другой стороны, их не может быть более двух, так как в этом случае
в особой вершине было бы более двух преследователей. Отсюда следует, что
в момент ![]() существуют ровно две голые вершины (обозначим их через
существуют ровно две голые вершины (обозначим их через
![]() ). Пусть
). Пусть ![]() - множество всех вершин, отличных от
- множество всех вершин, отличных от ![]() и
и ![]() . В силу леммы 1 каждая из вершин этого множества в
момент
. В силу леммы 1 каждая из вершин этого множества в
момент ![]() либо занята, либо является голой. Отсюда следует, что вершины
либо занята, либо является голой. Отсюда следует, что вершины
![]() , в них нет преследователей, а каждая из остальных вершин
множества
, в них нет преследователей, а каждая из остальных вершин
множества ![]() (которые мы будем обозначать через
(которые мы будем обозначать через
![]() занята одним преследователем. Вершине
занята одним преследователем. Вершине ![]() инцидентны два загрязненных ребра
инцидентны два загрязненных ребра
![]() и
и ![]() , остальные же инцидентные ей ребра должны быть
очищены. Заметим, что ребро
, остальные же инцидентные ей ребра должны быть
очищены. Заметим, что ребро ![]() , являющееся очищенным в момент
, являющееся очищенным в момент
![]() , в момент
, в момент ![]() окажется загрязненным, если к этому моменту в вершину
окажется загрязненным, если к этому моменту в вершину
![]() не придет преследователь из
не придет преследователь из ![]() . Все сказанное выше относительно
. Все сказанное выше относительно
![]() справедливо и для вершины
справедливо и для вершины ![]() . Заметим, что рассматриваемая ситуация
может возникнуть лишь для
. Заметим, что рассматриваемая ситуация
может возникнуть лишь для ![]() .
.
Покажем теперь, что ![]() . Предположим сначала, что в этот момент стала
особой вершина
. Предположим сначала, что в этот момент стала
особой вершина ![]() (
(![]() ) с
) с ![]() очищенными инцидентными ребрами.
Если
очищенными инцидентными ребрами.
Если ![]() , то в
, то в ![]() должны собраться все преследователи и, следовательно,
никакая другая вершина в момент
должны собраться все преследователи и, следовательно,
никакая другая вершина в момент ![]() не может стать особой. Если
не может стать особой. Если ![]() ,
то очищенным ребром, инцидентным
,
то очищенным ребром, инцидентным ![]() , может быть лишь
, может быть лишь ![]() или
или ![]() (при переходе преследователя из вершины
(при переходе преследователя из вершины ![]() в
в ![]() ребро
ребро ![]() оказывается в момент
оказывается в момент ![]() загрязненным). Пусть для определенности
очищенным ребром является
загрязненным). Пусть для определенности
очищенным ребром является ![]() . Оно оказалось очищенным в момент
. Оно оказалось очищенным в момент
![]() в результате перехода одного преследователя из
в результате перехода одного преследователя из ![]() в
в ![]() (при этом другой преследователь должен остаться в
(при этом другой преследователь должен остаться в ![]() ). Чтобы вершина
). Чтобы вершина
![]() могла стать особой в момент
могла стать особой в момент ![]() ,
все преследователи из вершин
,
все преследователи из вершин
![]() должны к этому моменту
перейти в
должны к этому моменту
перейти в ![]() . В этом случае
. В этом случае ![]() также является единственной особой вершиной
в момент
также является единственной особой вершиной
в момент ![]() . Осталось рассмотреть случай
. Осталось рассмотреть случай ![]() (из предыдущего ясно,
что
(из предыдущего ясно,
что ![]() ). В этом случае вершине
). В этом случае вершине ![]() в момент
в момент ![]() инцидентны два очищенных
ребра
инцидентны два очищенных
ребра ![]() и
и ![]() . Чтобы вершина
. Чтобы вершина ![]() могла стать особой в момент
могла стать особой в момент
![]() , в ней должны собраться
, в ней должны собраться ![]() преследователей (все, кроме двух,
находящихся в вершинах
преследователей (все, кроме двух,
находящихся в вершинах ![]() и
и ![]() ). Нетрудно убедиться, что и в этой ситуации
). Нетрудно убедиться, что и в этой ситуации
![]() - единственная особая вершина в момент
- единственная особая вершина в момент ![]() .
.
Предположим теперь, что в момент ![]() стала особой одна из вершин
стала особой одна из вершин
![]() , скажем,
, скажем, ![]() . Покажем, что и в этом
случае других особых вершин в момент
. Покажем, что и в этом
случае других особых вершин в момент ![]() быть не может. Это
утверждение очевидно, если преследователь, находящийся в момент
быть не может. Это
утверждение очевидно, если преследователь, находящийся в момент
![]() в вершине
в вершине ![]() , покидает ее. В противном случае будем
рассуждать следующим образом. Чтобы вершина
, покидает ее. В противном случае будем
рассуждать следующим образом. Чтобы вершина ![]() стала особой в
момент
стала особой в
момент ![]() , в нее необходимо перевести по крайней мере двух
преследователей (``нейтрализовать" загрязненные к моменту
, в нее необходимо перевести по крайней мере двух
преследователей (``нейтрализовать" загрязненные к моменту ![]() ребра
ребра ![]() ,
, ![]() и
и ![]() ). При этом
ясно, что преследователи, находящиеся в момент
). При этом
ясно, что преследователи, находящиеся в момент ![]() в вершинах
в вершинах
![]() , для этой цели использованы быть не могут.
Поведение же преследователей, находящихся в момент
, для этой цели использованы быть не могут.
Поведение же преследователей, находящихся в момент ![]() в
вершинах
в
вершинах ![]() и
и ![]() , должно быть следующим: для каждого
, должно быть следующим: для каждого ![]() по крайней мере один из преследователей, находящихся в
по крайней мере один из преследователей, находящихся в ![]() ,
должен перейти в
,
должен перейти в ![]() , причем если переходит ровно один
преследователь, то другой должен оставаться в
, причем если переходит ровно один
преследователь, то другой должен оставаться в ![]() . Теперь
становится ясным, что вершины
. Теперь
становится ясным, что вершины ![]() и
и ![]() не могут быть особыми
в момент
не могут быть особыми
в момент ![]() . То же можно сказать и о вершинах
. То же можно сказать и о вершинах
![]() .
.
Итак, если в момент ![]() становится особой одна из вершин
становится особой одна из вершин
![]() ,
, ![]() ,
,
![]() , то эта особая вершина - единственная.
Таким образом, осталось рассмотреть случай, когда в момент
, то эта особая вершина - единственная.
Таким образом, осталось рассмотреть случай, когда в момент ![]() могут стать
особыми лишь вершины
могут стать
особыми лишь вершины ![]() и
и ![]() .
Покажем, что на самом деле лишь одна из них может стать особой.
Предположим противное, и пусть
.
Покажем, что на самом деле лишь одна из них может стать особой.
Предположим противное, и пусть
![]() ,
, ![]() , -
все незанятые вершины в момент
, -
все незанятые вершины в момент ![]() .
Покажем, что каждая из этих вершин -
голая (в момент
.
Покажем, что каждая из этих вершин -
голая (в момент ![]() ). Если
). Если
![]() , то это утверждение
очевидно, поскольку в момент
, то это утверждение
очевидно, поскольку в момент ![]() вершина
вершина ![]() инцидентна
загрязненным ребрам
инцидентна
загрязненным ребрам ![]() и
и ![]() .
В противном случае вершина
.
В противном случае вершина ![]() оказывается голой в момент
оказывается голой в момент ![]() в силу леммы 1.
в силу леммы 1.
Таким образом, в момент ![]() в особых вершинах
в особых вершинах ![]() находится не менее
находится не менее
![]() преследователей. Для преследователей, стоящих в
этот момент в неособых вершинах, остается
преследователей. Для преследователей, стоящих в
этот момент в неособых вершинах, остается ![]() вершин, каждая из которых
должна быть занята (иначе, незанятых вершин оказывается больше
вершин, каждая из которых
должна быть занята (иначе, незанятых вершин оказывается больше ![]() ).
Отсюда следует, что
).
Отсюда следует, что
Итак, если предположить, что особыми (в момент ![]() ) являются обе
вершины
) являются обе
вершины ![]() и
и ![]() , то в этот момент в каждой занятой вершине
находится ровно один преследователь. Осталось выяснить, каким
образом вершина
, то в этот момент в каждой занятой вершине
находится ровно один преследователь. Осталось выяснить, каким
образом вершина ![]() , особая в момент
, особая в момент ![]() , осталась особой в
момент
, осталась особой в
момент ![]() . Это могло произойти лишь следующим образом: два
преследователя, находящиеся в момент
. Это могло произойти лишь следующим образом: два
преследователя, находящиеся в момент ![]() в вершине
в вершине ![]() ,
перешли в
,
перешли в ![]() и
и ![]() , а в вершину
, а в вершину ![]() перешел ровно один
преследователь из
перешел ровно один
преследователь из ![]() (чтобы в момент
(чтобы в момент ![]() ``нейтрализовать"
единственное инцидентное
``нейтрализовать"
единственное инцидентное ![]() загрязненное ребро
загрязненное ребро ![]() ).
Однако в этом случае нетрудно убедиться, что вершина
).
Однако в этом случае нетрудно убедиться, что вершина ![]() не
может быть особой в момент
не
может быть особой в момент ![]() . Получили противоречие.
. Получили противоречие.
Таким образом, доказано, что в процессе реализации программы ![]() не может
возникнуть более двух особых вершин и, следовательно, эта программа
не может быть
выигрывающей.
не может
возникнуть более двух особых вершин и, следовательно, эта программа
не может быть
выигрывающей.
![]()
Д о к а з а т е л ь с т в о.
(T1). Импликация ![]() является следствием
теорем 10 и 3.
является следствием
теорем 10 и 3.
![]() : Опишем выигрывающую программу трех преследователей при
: Опишем выигрывающую программу трех преследователей при
![]() . Обозначим через
. Обозначим через ![]() вершины графа
вершины графа ![]() и через
и через
![]() - цикл
- цикл ![]() . Преследователь
. Преследователь ![]() движется в выбранном
направлении по циклу
движется в выбранном
направлении по циклу ![]() с постоянной максимальной (единичной) скоростью.
Преследователь
с постоянной максимальной (единичной) скоростью.
Преследователь ![]() (
(![]() ) движется по ребру
) движется по ребру
![]() (
(![]() ). Действия преследователей синхронизированы
следующим образом:
). Действия преследователей синхронизированы
следующим образом:
![]() встречается с
встречается с ![]() в
в
![]() и
и ![]() ;
; ![]() встречает
встречает ![]() в
в
![]() и
и ![]() .
.
Если убегающий не покидает
![]() , то за время
, то за время ![]() он будет пойман преследователем
он будет пойман преследователем ![]() .
С другой стороны,
учитывая действия игроков
.
С другой стороны,
учитывая действия игроков ![]() и
и ![]() ,
можно убедиться, что покинув цикл
,
можно убедиться, что покинув цикл ![]() , убегающий, уклоняющийся от встречи
с этими игроками, должен на
, убегающий, уклоняющийся от встречи
с этими игроками, должен на ![]() возвратиться. При этом расстояние
между ним и преследователем
возвратиться. При этом расстояние
между ним и преследователем ![]() уменьшается.
уменьшается.
(T2). Пусть ![]() - вершины
- вершины ![]() . Определим
программу, в которой преследователи
. Определим
программу, в которой преследователи ![]() и
и ![]() движутся с
максимальной скоростью по следующим маршрутам:
движутся с
максимальной скоростью по следующим маршрутам:
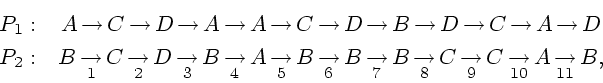
Проверка того, что указанная программа является выигрывающей при
![]() проста и нами опускается.
проста и нами опускается.
![]()
Д о к а з а т е л ь с т в о.
![]() : Рассмотрим произвольную дискретную программу
: Рассмотрим произвольную дискретную программу ![]() четырех преследователей на графе октаэдра
четырех преследователей на графе октаэдра ![]() . Мы докажем, что при
. Мы докажем, что при
![]() эта программа не является выигрывающей.
эта программа не является выигрывающей.
Поскольку всякая вершина октаэдра смежна всем остальным вершинам, за исключением одной, справедлива следующая лемма.
Мы покажем, что в программе
![]() все числа
все числа ![]() , а потому эта программа
не может быть выигрывающей.
, а потому эта программа
не может быть выигрывающей.
Очевидно, что ![]() . Докажем, что
. Докажем, что
![]() влечет
влечет ![]() .
Заметим, что по лемме 2 в момент
.
Заметим, что по лемме 2 в момент
![]() имеется не более двух особых вершин. Следовательно,
если
имеется не более двух особых вершин. Следовательно,
если ![]() , то
, то ![]() .
.
Предположим, что ![]() и
и ![]() , т.е. одна особая вершина
, т.е. одна особая вершина
![]() - старая, а две особые вершины
- старая, а две особые вершины
![]() ,
, ![]() - новые.
По лемме 2 в момент
- новые.
По лемме 2 в момент ![]() вершины
вершины ![]() ,
, ![]() являются 2-особыми, поэтому
являются 2-особыми, поэтому
![]() - 0-особая. Таким образом,
- 0-особая. Таким образом,
![]() .
С другой стороны, согласно
лемме 1
.
С другой стороны, согласно
лемме 1 ![]() и мы доказали, что
и мы доказали, что
![]() влечет
влечет ![]() .
.
Рассмотрим последний возможный случай ![]() .
Сначала мы докажем вспомогательное утверждение.
.
Сначала мы докажем вспомогательное утверждение.
Д о к а з а т е л ь с т в о
л е м м ы ![]() Если
Если ![]() , то
в момент
, то
в момент ![]() имеются две новые 2-особые вершины. В то же время,
согласно лемме 1 все остальные вершины голые.
Нетрудно убедиться, что такая ситуация не может возникнуть,
и для доказательства леммы достаточно рассмотреть случай
имеются две новые 2-особые вершины. В то же время,
согласно лемме 1 все остальные вершины голые.
Нетрудно убедиться, что такая ситуация не может возникнуть,
и для доказательства леммы достаточно рассмотреть случай
![]() .
Для этого случая возможны варианты:
.
Для этого случая возможны варианты:
(I)Из двух особых в момент ![]() вершин одна является новой, а вторая старой.
вершин одна является новой, а вторая старой.
(II)Обе две особые в момент ![]() вершины являются новыми.
вершины являются новыми.
Покажем, что первый вариант не может реализоваться.
Предположим противное: в момент
![]() имеется одна старая особая вершина
имеется одна старая особая вершина ![]() и одна новая -
и одна новая - ![]() . Поскольку
. Поскольку
![]() (лемма 2),
то
(лемма 2),
то ![]() (лемма 1). Из леммы 3
следует, что
(лемма 1). Из леммы 3
следует, что
![]() и, снова используя лемму 1,
получаем
и, снова используя лемму 1,
получаем ![]() .
Лемма 3 влечет
.
Лемма 3 влечет
![]() ;
таким образом,
;
таким образом,
![]() .
Но как следует из леммы 1, в возникшей ситуации все
остальные вершины обязаны быть голыми, т.е.
.
Но как следует из леммы 1, в возникшей ситуации все
остальные вершины обязаны быть голыми, т.е.
![]() , что противоречит лемме 3.
, что противоречит лемме 3.
Нами доказано, что если ![]() и
и ![]() , то
должны быть
, то
должны быть
![]() и имеются две новые особые
вершины
и имеются две новые особые
вершины ![]() ,
, ![]() .
По лемме 2 эти вершины являются 2-особыми
и
.
По лемме 2 эти вершины являются 2-особыми
и ![]() (отметим, что
(отметим, что
![]() не может быть голой).
Подобная ситуация может возникнуть, только если
вершины
не может быть голой).
Подобная ситуация может возникнуть, только если
вершины ![]() и
и ![]() смежны и каждая из них смежна двум голым
вершинам. Поскольку
смежны и каждая из них смежна двум голым
вершинам. Поскольку
![]() и
и ![]() являются 2-особыми и
являются 2-особыми и ![]() , мы заключаем, что
ребро
, мы заключаем, что
ребро ![]() очищено. Более того, легко проверяется, что
ребра
очищено. Более того, легко проверяется, что
ребра ![]() и
и ![]() тоже очищены. Таким образом,
цикл, порождаемый вершинами
тоже очищены. Таким образом,
цикл, порождаемый вершинами ![]() , в момент
, в момент ![]() очищен и
очищен и
![]() ,
,
![]() . Заметим, что такая
ситуация осуществима. Но теперь ясно, что любые действия
преследователей из данной позиции приводят к случаю
. Заметим, что такая
ситуация осуществима. Но теперь ясно, что любые действия
преследователей из данной позиции приводят к случаю ![]() и
лемма 4 доказана.
и
лемма 4 доказана. ![]()
Из леммы 4 следует, что если
![]() , то
, то ![]() и
и ![]() .
Поэтому мы заключаем, что в программе
.
Поэтому мы заключаем, что в программе
![]() все числа
все числа ![]() и эта программа не может быть
выигрывающей.
и эта программа не может быть
выигрывающей.
Итак,
![]() при
при ![]() и по теореме 7
и по теореме 7
![]() при
при ![]() .
.
![]() :
Опишем выигрывающую при
:
Опишем выигрывающую при ![]() программу четырех преследователей.
Преследователь
программу четырех преследователей.
Преследователь ![]() ,
,
![]() , движется по циклу
, движется по циклу ![]() длины 3 следующим образом (см. рисунок):
длины 3 следующим образом (см. рисунок):
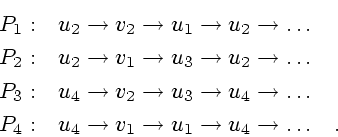
Если убегающий не покидает цикл
![]() , то на протяжении
, то на протяжении
![]() он будет пойман
преследователем
он будет пойман
преследователем ![]() (
(![]() ). С другой стороны, смена циклов не помогает
убегающему уклониться от поимки.
В самом деле, если убегающий переходит с цикла
). С другой стороны, смена циклов не помогает
убегающему уклониться от поимки.
В самом деле, если убегающий переходит с цикла ![]() на цикл
на цикл ![]() в некоторый момент времени
в некоторый момент времени ![]() (такой переход может произойти
только в вершине октаэдра), то в момент
(такой переход может произойти
только в вершине октаэдра), то в момент ![]() он ``равноудален" от
преследователей
он ``равноудален" от
преследователей ![]() и
и ![]() .
. ![]()
Д о к а з а т е л ь с т в о.
(C1) ![]() : Покажем, что
: Покажем, что
![]() .
Рассмотрим произвольную дискретную программу поиска четырех
преследователей
.
Рассмотрим произвольную дискретную программу поиска четырех
преследователей ![]() и докажем, что программа
и докажем, что программа ![]() не может
быть выигрывающей при
не может
быть выигрывающей при ![]() .
.
Нетрудно убедиться в справедливости следующей леммы.
a) Если в момент ![]() имеется одна 0-особая вершина,
имеется одна 0-особая вершина,
то
![]() .
.
b) Если в момент ![]() имеется две 0-особые вершины, то
имеется две 0-особые вершины, то
![]() .
.
Для доказательства того, что программа не является выигрывающей,
мы покажем, что все числа
![]() .
.
Предположим, что в начальный момент времени все преследователи
находятся в одной вершине - единственной особой вершине в данный
момент. Докажем, что ![]() влечет
влечет ![]() . Отметим,
что из леммы 2 следует, что в момент
. Отметим,
что из леммы 2 следует, что в момент ![]() не более двух
особых вершин являются новыми. Поэтому если
не более двух
особых вершин являются новыми. Поэтому если ![]() , то
, то
![]() .
.
Предположим, что ![]() , но
, но ![]() .
Тогда
.
Тогда ![]() . Более того, в момент
. Более того, в момент ![]() две особые вершины
две особые вершины
![]() ,
, ![]() - старые и две особые вершины
- старые и две особые вершины ![]() ,
, ![]() - новые.
Поскольку
- новые.
Поскольку ![]() ,
, ![]() являются 2-особыми в момент
являются 2-особыми в момент ![]() , то
вершины
, то
вершины ![]() ,
, ![]() в этот же момент должны быть
0-особыми.
Лемма 1 влечет
в этот же момент должны быть
0-особыми.
Лемма 1 влечет
![]() ; с другой стороны,
; с другой стороны,
![]() (лемма 5).
Таким образом, если
(лемма 5).
Таким образом, если ![]() , то
, то ![]() .
.
Для изучения случая ![]() докажем еще одну лемму.
докажем еще одну лемму.
Д о к а з а т е л ь с т в о. Если ![]() , то в момент
, то в момент ![]() множество особых вершин
состоит их одной старой вершины
множество особых вершин
состоит их одной старой вершины ![]() и двух новых
и двух новых
![]() ,
, ![]() . Из леммы 2 следует, что
вершины
. Из леммы 2 следует, что
вершины ![]() и
и ![]() являются 2-особыми в момент
являются 2-особыми в момент ![]() ;
следовательно, в этот момент
;
следовательно, в этот момент ![]() является 0-особой.
В силу леммы 1
является 0-особой.
В силу леммы 1 ![]() , в то же время лемма 5
влечет
, в то же время лемма 5
влечет ![]() . Поэтому
. Поэтому
![]() .
.
В этом случае возможен один из вариантов:
(I)
Из трех особых в момент
![]() вершин две старые и одна новая.
вершин две старые и одна новая.
(II)
Из трех особых в момент
![]() вершин одна старая и две новые.
вершин одна старая и две новые.
Покажем, что вариант (I) невозможен.
Предположим, что в момент
![]() особые вершины
особые вершины
![]() ,
, ![]() являются старыми, а вершина
являются старыми, а вершина
![]() новая.
По лемме 2
новая.
По лемме 2
![]() .
В этой ситуации возникает четыре случая.
.
В этой ситуации возникает четыре случая.
a)
![]() .
По лемме 5
.
По лемме 5 ![]() и лемма 1
влечет
и лемма 1
влечет ![]() .
.
b) ![]() ,
, ![]() .
По лемме 1
.
По лемме 1 ![]() , тогда по лемме 5
, тогда по лемме 5
![]() .
.
c) ![]() ,
, ![]() . В силу лемм 1
и 5 имеем
. В силу лемм 1
и 5 имеем ![]() .
Три вершины куба смежны вершине
.
Три вершины куба смежны вершине ![]() ,
и
,
и ![]() не может быть голой.
Следовательно,
не может быть голой.
Следовательно, ![]() смежна
смежна ![]() . Тогда
вершина
. Тогда
вершина ![]() инцидентна двум загрязненным
(в момент
инцидентна двум загрязненным
(в момент ![]() ) ребрам и не может быть особой.
) ребрам и не может быть особой.
d)
![]() ,
, ![]() .
В этом случае
.
В этом случае
![]() . В момент
. В момент ![]() вершина
вершина ![]() смежна как минимум двум очищенным ребрам, концы которых
не принадлежат
смежна как минимум двум очищенным ребрам, концы которых
не принадлежат ![]() .
А потому
.
А потому ![]() смежна
смежна ![]() и
и ![]() .
По той же причине
.
По той же причине
![]() смежна
смежна ![]() и
и ![]() . Тогда
вершины
. Тогда
вершины ![]() ,
, ![]() ,
, ![]() порождают цикл длины три в
порождают цикл длины три в ![]() , что невозможно.
, что невозможно.
Мы доказали, что если
![]() и
и ![]() , то возможен только вариант (II), т.е.
существуют вершины
, то возможен только вариант (II), т.е.
существуют вершины
![]() ,
,
![]() и две новых вершины
и две новых вершины
![]() ,
,
![]() . По лемме 1
все вершины, за исключением
. По лемме 1
все вершины, за исключением
![]() ,
,![]() ,
,![]() и
и ![]() являются голыми в момент
являются голыми в момент ![]() , а потому
, а потому
![]() . Также вершины
. Также вершины ![]() ,
,![]() ,
,![]() смежны
смежны ![]() . Отметим, что такая ситуация возможна.
. Отметим, что такая ситуация возможна.
Теперь ясно, что всякие действия преследователей в данной позиции
приводят к случаю
![]() и лемма 6 доказана.
и лемма 6 доказана. ![]()
Из леммы 6 следует, что если ![]() , то
, то
![]() и
и ![]() .
Таким образом, для программы
.
Таким образом, для программы ![]() все числа
все числа
![]() и
и ![]() не может быть выигрывающей.
не может быть выигрывающей.
Итак,
![]() при
при ![]() и по теореме 6
и по теореме 6
![]() при
при ![]() .
.
![]() : Предъявим выигрывающую при
: Предъявим выигрывающую при ![]() программу
четырех преследователей. Каждый из преследователей
программу
четырех преследователей. Каждый из преследователей ![]() ,
,
![]() , движется по циклу
, движется по циклу ![]() длины четыре
согласно следующей схеме (см. рисунок):
длины четыре
согласно следующей схеме (см. рисунок):
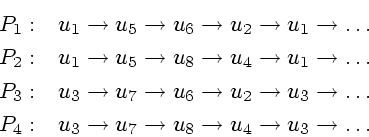
Как и в теореме 12, нетрудно убедиться в том, что за время
![]() убегающий будет пойман.
убегающий будет пойман.
(C2)
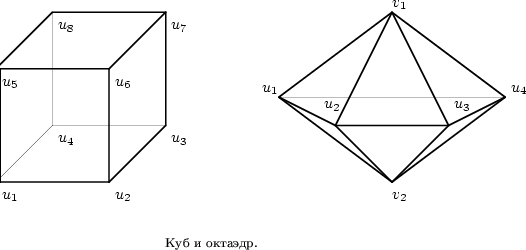
Обозначим через ![]() ,
,
![]() , вершины графа
, вершины графа
![]() (см. рисунок).
Определим маршруты преследователей:
(см. рисунок).
Определим маршруты преследователей:
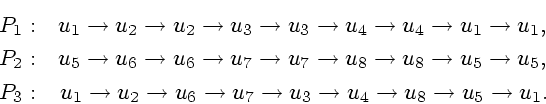
Каждый из преследователей проходит по указанному маршруту
![]() раз. Легко доказывается, что при
раз. Легко доказывается, что при
![]() данная программа будет выигрывающей.
В самом деле,
преследователи
данная программа будет выигрывающей.
В самом деле,
преследователи ![]() и
и ![]() вынуждают убегающего
покинуть ребра циклов
вынуждают убегающего
покинуть ребра циклов
![]() и
и
![]() . Но тогда убегающий
ловится игроком
. Но тогда убегающий
ловится игроком ![]() .
.
(C3)
Обозначим через ![]() ,
,
![]() , вершины графа
, вершины графа
![]() (см. рисунок).
Определим траектории игроков:
(см. рисунок).
Определим траектории игроков:
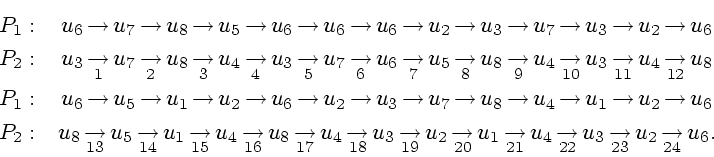
Доказательство того, что при ![]() программа является
выигрывающей, просто и оставляется читателю.
программа является
выигрывающей, просто и оставляется читателю. ![]()