2. Случай $\mathbf \mu =\infty$, $\mathbf \varepsilon \ge 0$

В дальнейшем мы будем использовать следующие известные факты. Первая используемая нами теорема была доказана в [2].

Теорема 1.   Если $\mathrm{deg}(\Gamma )\ge 3$, то $S_{\infty}^{0}(\Gamma )\ge \mathrm{deg}(\Gamma ) +1$, где $\mathrm{deg}(\Gamma )$ - наименьшая из степеней вершин графа $\Gamma$.

Следующая теорема (см. [1]) дает оценку ``близости" величин $S_{\infty}^{\varepsilon}(\Gamma )$ и $S_{\infty}^{0}(\Gamma )$ при малых $\varepsilon$.

Теорема 2.   Пусть $l$ - длина наименьшего ребра графа $\Gamma$. Тогда

1. $S_{\infty}^{\varepsilon}(\Gamma )=S_{\infty}^{0}(\Gamma )$ при $0\le\varepsilon < 0.25l$;
2. $S_{\infty}^{\varepsilon}(\Gamma )\ge S_{\infty}^{0}(\Gamma )-1$ при $0.25l\le\varepsilon < 0.5l$.

Мы готовы приступить к доказательству нашего первого факта об остове тетраэдра.

Теорема 3.  

$$S_{\infty}^{\varepsilon}(T) =\left\{ \begin{array}{rl} 4 &\m... ...\ [1ex] 1 &\mbox{ при }\ 1.5\le\varepsilon. \end{array}\right.$$

Д о к а з а т е л ь с т в о. Заметим, что во всех случаях выигрывающая программа строится достаточно просто: четыре преследователя ловят убегающего при $\varepsilon \ge 0$, три при $\varepsilon \ge 0.25$, два при $\varepsilon \ge 0.5$ и один преследователь ловит при $\varepsilon \ge 1.5$. Поэтому при $0 \le \varepsilon < 0.5$ утверждение теоремы является следствием теорем 1 и 2, а случай $\varepsilon \ge 0.5$ тривиален. $\Box$

Доказанная теорема является частным случаем теоремы 8, посвященной полным графам.

Для решения задач поиска для графов $C$ и $O$ нам понадобятся более сильные результаты.

Упорядочением вершин графа $\Gamma$ будем называть взаимно-однозначное отображение

$$f\colon V(\Gamma )\to\{1,\dots,\vert V(\Gamma )\vert\}.$$

Для упорядочения $f$ графа $\Gamma$ определим величины

$$\mathrm{cw}_i (\Gamma , f)=\vert\{(u,v)\in E(\Gamma )\colon f(u)\le i, f(v)>i\}\vert$$

и

$$\mathrm{cw}(\Gamma , f)=\max_{{i}\in\{{1},\dots, {\vert V(\Gamma )\vert}\}} \mathrm{cw}_i (\Gamma , f).$$

Шириной разреза $\mathrm{cw}(\Gamma )$ графа $\Gamma$ называется наименьшее из чисел $\mathrm{cw}(\Gamma , f)$, где минимум берется по всевозможным упорядочениям $f$ вершин
графа $\Gamma$.

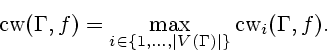
Мы будем ссылаться на следующую теорему о связи поискового числа и ширины разреза [16]. Напомним, что степенью вершины называется число смежных ей вершин.

Теорема 4.   Если степень всякой вершины графа $\Gamma$ не превосходит трех, то $S_{\infty}^{0}(\Gamma )=\mathrm{cw}(\Gamma )$.

Обозначим через $\Gamma ^{\prime}(v)$ подграф графа $\Gamma$, порождаемый множеством смежных $v$ вершин, а через $n_k (\Gamma , v)$ - число компонент связности графа $\Gamma ^{\prime}(v)$ с ровно $k$ вершинами.

Определим

$$c(\Gamma , v)\stackrel{\bigtriangleup}{=} \sum_{k=1}^{\infty} n_k (\Gamma , v) \Big\lceil \frac{k}{2} \Big\rceil$$

и

$$c(\Gamma )\stackrel{\bigtriangleup}{=}\min_{v\in V(\Gamma )} c(\Gamma , v).$$

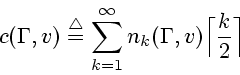
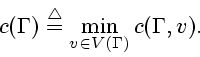
Доказательство следующей теоремы приводится в [4].

Теорема 5.   Пусть $l$ - длина наименьшего ребра в $\Gamma$ и пусть $0\le \varepsilon < l$. Тогда

1. $S_{\infty}^{\varepsilon}(\Gamma )\ge c(\Gamma )$;
2. если для всякой вершины $v\in V(\Gamma )$ все коэффициенты $n_k (\Gamma , v)$ с нечетными номерами $k$ равны 0, то $S_{\infty}^{\varepsilon}(\Gamma )\ge c(\Gamma )+1$.

Вычислим числа $S_{\infty}^{\varepsilon}$ для графа куба и графа октаэдра.

Теорема 6.  

$$S_{\infty}^{\varepsilon}(C) =\left\{ \begin{array}{rl} 5&\mb... ...3,\\ [1ex] 1&\mbox{ при }\ 3\le\varepsilon. \end{array}\right.$$

Д о к а з а т е л ь с т в о. Заметим, что во всех случаях соответствующая выигрывающая программа строится без труда.

Так как всякая вершина графа куба $C$ имеет степень три, то по теореме 4 $\mathrm{cw}(C)=S_{\infty}^{0}(C)$. Упорядочение $f$ вершин графа $C$ такое, что $\mathrm{cw}(C,f)=5$ приводится на рисунке (мы полагаем $f(u_i)=i$). Отметим, что для всякого упорядочения $f$ первые три вершины ``связаны" с оставшимися вершинами как минимум пятью ребрами, поэтому $\mathrm{cw}(C)\ge 5$. Нижние оценки следуют: для $0 \le \varepsilon < 0.5$ - из теоремы 2, для $0.5\le\varepsilon < 1$ - из теоремы 5. Случай $1\le\varepsilon <3$ тривиален. $\Box$

Теорема 7.  

$$S_{\infty}^{\varepsilon}(O) =\left\{ \begin{array}{rl} 5,&\m... ...,\\ [1ex] 1,&\mbox{ при }\ 2\le\varepsilon. \end{array}\right.$$

Д о к а з а т е л ь с т в о. По теореме 1 $S_{\infty}^{0}(O) \ge 5$. Остальные оценки доказываются как в теореме 6.$\Box$

Для полных графов наблюдается интересный эффект - ``скачок" величины $S_{\infty}^{\varepsilon}$ при переходе параметром $\varepsilon$ отметки $1/2$.

Теорема 8.  

$$S_{\infty}^{\varepsilon}(K_n) =\left\{ \begin{array}{ll} n &... ...\ [1ex] 1 &\mbox{ при }\ 1.5\le\varepsilon. \end{array}\right.$$

Д о к а з а т е л ь с т в о. Докажем, что $S_{\infty}^{\varepsilon}(K_n)= \Big\lceil n/2 \Big\rceil$ при $\varepsilon \in$
$[1/2,1)$. Во всех остальных случаях соответствующие выигрывающие программы строятся без труда, а необходимые оценки снизу для $\varepsilon \in [0,1/2)$ легко следуют из теоремы 2. Если $n=2l+1$, $l\in \{2,3,\dots\}$, то в силу утверждения 2 теоремы 5

$$S_{\infty}^{\varepsilon}(K_n)\ge \Big\lceil (n-1)/2 +1\Big\rceil=l+1 = \Big\lceil n/2 \Big\rceil.$$

Если же $n=2l$, $l\in \{2,3,\dots\}$, то в силу утверждения 1 теоремы 5

$$S_{\infty}^{\varepsilon}(K_n)\ge \Big\lceil (n-1)/2 \Big\rceil=l = \Big\lceil n/2 \Big\rceil.$$

Таким образом, для любых $\varepsilon \in [1/2,1)$ и $n>3$ величина $S_{\infty}^{\varepsilon}(K_n)\ge \Big\lceil n/2 \Big\rceil$. Для того чтобы доказать противоположное неравенство, опишем выигрывающую программу для $\Big\lceil n/2 \Big\rceil$ преследователей. Пусть $\Big\lceil n/2 \Big\rceil-1$ преследователя стоят в серединах ребер, ``контролируя" $2\Big\lceil n/2 \Big\rceil -2$ различных вершин. Тогда нетрудно убедиться, что одного преследователя достаточно, чтобы очистить оставшуюся часть графа $K_n$. $\Box$